概要
主成分分析では、複数の特徴量を持つデータセットから、そのデータセットの特徴を最もよく表す特徴量軸を発見していく。
ここで「特徴を最もよく表す」ことを数学的に「最も分散が大きくなる」と定義する。そして、分散が最も大きくなるような方向を探すことを目的とする。
ある軸に沿った分散が大きくなるということは、その軸に沿った性質のバリエーションが多いことになる。逆に分散が小さい場合は、その性質を表す数量によっては各データの特徴の違いが判別しにくい。
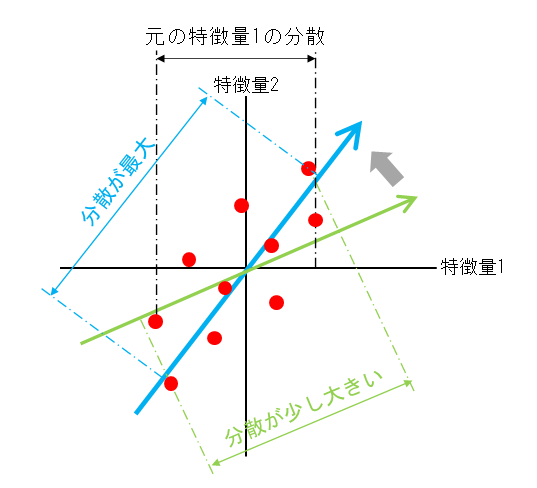
主成分分析では、分散が最大となるような軸の方向を発見することが目的となる。この軸は元の特徴量の線形和で表現されるもので、各特徴量の係数は、それぞれの特徴量の寄与を表す。
(1) 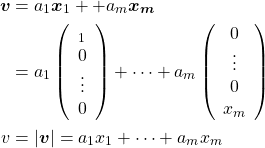
以後、複数の特徴量を持つデータを、特徴量を成分とするベクトルでx表し、多数のベクトルデータxiがデータセットを構成しているとする。
最大化すべき分散の導出
多数のデータの中のデータiが空間内の点に対応し、その位置ベクトルをxiであるとする。このxiの成分が特徴量に対応する。長さが1のあるベクトルdが与えられたとき、xiのdへの射影の長さは以下のように計算される。
(2) ![]()
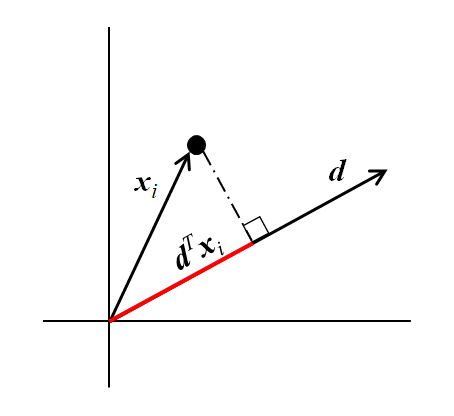
たとえば特徴量が2つなら、2次元で以下のような計算になる。
(3) ![]()
(4) ![]()
n個のデータ(i = 1~n)について、射影の平均は以下のように計算される。これは全データのベクトルdの方向に沿った値の平均となる。
(5) ![]()
これも2次元の場合で確認すると以下の通り。
(6) ![Rendered by QuickLaTeX.com \begin{align*} E(x_{i | \boldsymbol{d}} ) &= E\left[ (d1, d2) \left( \begin{array}{c} x_{i1} \\ x_{i2} \end{array} \right) \right] = (d_1, d_2) \left( \begin{array}{c} E(x_{i1}) \\ E(x_{i2}) \end{array} \right) \\ &= (d_1, d_2) \left( \begin{array}{c} \mu_{i1} \\ \mu_{i2} \end{aray} \right) \end{align*}](http://taustation.com/wp1/wp-content/ql-cache/quicklatex.com-6d6230f138fc3fa7ed12c321cb886709_l3.png)
式(5)を使ってベクトルdの方向に沿ったデータの分散を計算する。
(7) ![Rendered by QuickLaTeX.com \begin{align*} V( x_{i | \boldsymbol{d}} ) &= V \left( \boldsymbol{d}^T \boldsymbol{x}_i \right) \\ &= E \left[ \left( \boldsymbol{d}^T \boldsymbol{x}_i - E \left( \boldsymbol{d}^T \boldsymbol{x}_i \right) \right)^2 \right] \\ &= E \left[ \left( {\boldsymbol{d}}^T \left( \boldsymbol{x}_i - E(\boldsymbol{x}_i) \right) \right)^2 \right] \\ &= E \left[ {\boldsymbol{d}}^T (\boldsymbol{x}_i - \boldsymbol{\mu}_i ) (\boldsymbol{x}_i - \boldsymbol{\mu}_i )^T \boldsymbol{d} \right] \\ &= \boldsymbol{d}^T E\left[ (\boldsymbol{x}_i - \boldsymbol{\mu}_i ) (\boldsymbol{x}_i - \boldsymbol{\mu}_i )^T \right] \boldsymbol{d} \\ &= \boldsymbol{d}^T \boldsymbol{\Sigma} \boldsymbol{d} \end{align*}](http://taustation.com/wp1/wp-content/ql-cache/quicklatex.com-124a18127aad98b510df2af2181173ee_l3.png)
中央の平均の項が共分散行列Σとなっていることに留意。これより、あるベクトルが与えられたとき、その方向に沿った全データの成分の分散が、そのベクトルと元のデータの共分散行列を使って求めることができる。
こちらを2次元で確認すると以下の通り。
(8) ![Rendered by QuickLaTeX.com \begin{align*} &E\left[ (\boldsymbol{x}_i - \boldsymbol{\mu}_i ) (\boldsymbol{x}_i - \boldsymbol{\mu}_i )^T \right] \\ &= E \left[ \left( \begin{array}{c} x_{i1} - \mu_1 \\ x_{i2} - \mu_2 \end{array} \right) (x_{i1} - \mu_1, x_{i2} - \mu_2) \right] \\ &= \left[ \begin{array}{cc} (x_{i1} - \mu_1)^2 & (x_{i1} - \mu_1)(x_{i2} - \mu_2) \\ (x_{i2} - \mu_2)(x_{i1} - \mu_1) & (x_{i2} - \mu_2)^2 \end{array} \right] \end{align*}](http://taustation.com/wp1/wp-content/ql-cache/quicklatex.com-6f7b889cad8cd2284e27cc9de5f9ede2_l3.png)
分散の最大化
式(8)で計算された分散が最大となるようにベクトルdの方向を決定する。このとき、dの大きさが1であるという制約条件があるため、問題は制約条件付きの最大化問題となる。
(9) ![]()
これをLagrangeの未定乗数法で解いていく。。
(10) 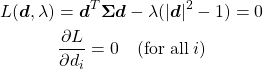
Lagrange関数の第1項については、
(11) 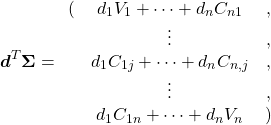
より、以下のような長い式になる。
(12) 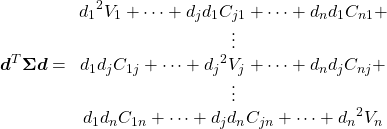
また第2項の括弧の中については以下のようになる。
(13) ![]()
これらを前提に、Lをdjで微分すると以下のようになる。
(14) ![]()
全てのdjについて考慮した連立方程式を行列形式で表すと以下のようになる。
(15) ![]()
1つ目の式は共分散行列に関する固有値問題の式で、di (i=1~n)とλのn+1個の変数に対してn個の式となる。これに先ほど脇に置いていたdの大きさに関する制約式を加えて式の数もn+1個となり、dとλが求められる。
特徴量が2つの場合
特徴量が2つの場合を考え、以下のように記号を定義する。
(16) ![]()
このとき、分散を最大化する方向の単位ベクトルdを求める方程式は以下のようになる。
(17) 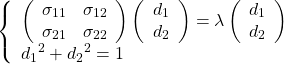
1つ目の式を解くと、
(18) ![]()
この方程式は不定なのでd1、d2それぞれは求められないが、μ = d2/d1は計算できる。これは固有ベクトルの方向が定まる。具体的には下記の通り。
(19) 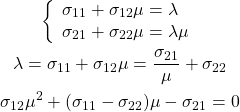
これを解いてベクトルdの方向が定まる。これに制約条件|d|2 =1を加味することで、大きさ1の単位ベクトルとしてdが決定される。
この解き方は最大化問題ではないので、連立方程式から2つの固有ベクトルと固有値が求まる。
第2主成分以降
一般的な固有値問題では、元の変数と同じ数の固有ベクトルと固有値のセットが求まるが、最大化問題として解いた場合には主成分が1つだけ求まる。
scikit-learnのPCAインスタンス生成時にn_componentsで主成分の数に制約をかけることができるが、このことから、PCA.fit()の実行時には連立方程式を解いているのではなく、最大化問題で1つずつ主成分を計算しているのではないかと思われる。
第2主成分以降の計算についての紹介はあまり見られないが、以下の手順と考えらえれる。
- 各データについて、第1主成分の方向への射影を計算
- その射影の符号を逆にしたベクトルを各データに加える
- これで第1主成分に沿ったばらつきが全てゼロになるので、残りの成分の中で最大となるベクトルの方向を計算し、第2主成分とする
- 以上を繰り返し、順次最大主成分沿いの情報を消しながら、各主成分を計算
主成分の意味
主成分の意味の一つに、元のデータを構成する成分という捉え方がある。
たとえば特徴量の数がnである元データXがあり、主成分の数をm(<= n)でモデルを構築するとする。scikit-learnでPCAのインスタンスを生成するのにn_components=mと指定し、fit(X)を実行すると、m個の主成分が生成される。この主成分は共分散行列に対する固有ベクトルであり、要素数n個(特徴量数に等しい)の1次元配列がm行(主成分の数に等しい)並んだ2次元配列として、PCAインスタンスのプロパティーcomponents_に保存される。
(20) ![Rendered by QuickLaTeX.com \begin{equation*} \tt{components\_} = \left[ \begin{array}{ccc} (p_{0, 0} & \cdots & p_{0, n-1} ) \\ & \vdots &\\ (p_{m-1, 0} & \cdots & p_{m-1, n-1}) \end{array} \right] = \left[ \begin{array}{c} \boldsymbol{p}_0 \\ \vdots \\ \boldsymbol{p}_m \end{array} \right] \end{equation*}](http://taustation.com/wp1/wp-content/ql-cache/quicklatex.com-d9be42d7f003af87c8a132ea3f54bba8_l3.png)
元のデータは、各主成分(固有ベクトル)の重み付き和として表現される。
(21) ![]()
この様子を2次元で示したのが以下の図で、直行する2つの主成分から元データの1つxが定まる。
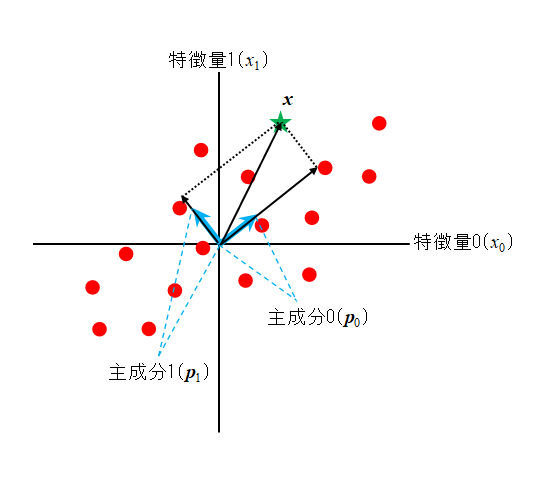
xの主成分1、2の方向の大きさはxの各主成分に対する射影で、それらの長さはxと各主成分の内積で得られる。
(22) ![]()