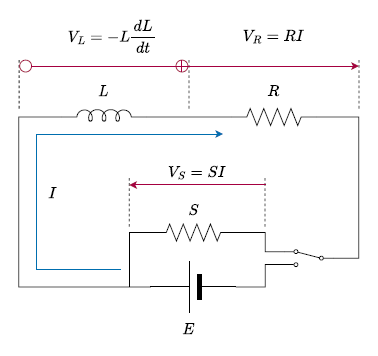
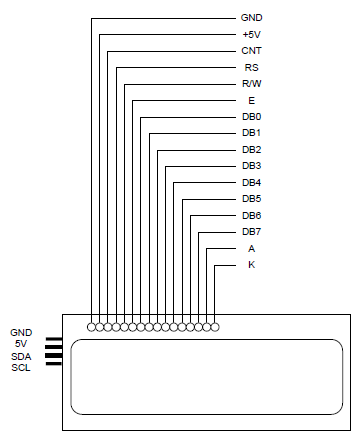
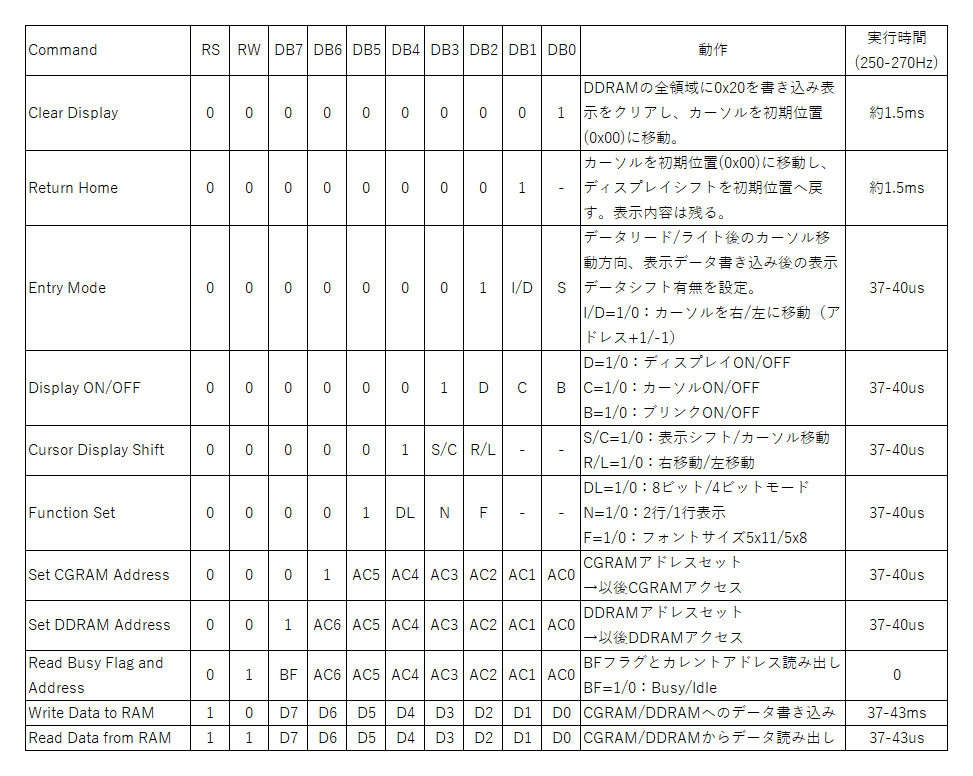
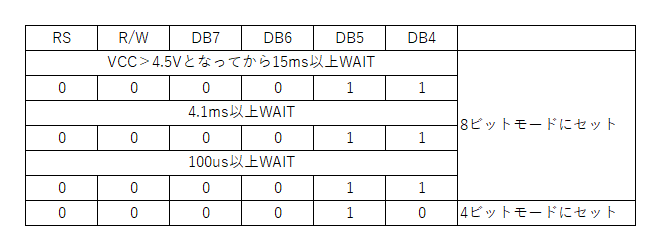
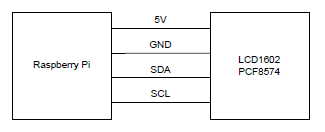
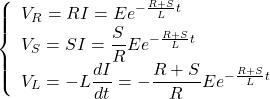放物線の焦点

2023-06-23 / tau / コメントする

概要

放物線が、その対称軸に平行な線に対して焦点を持つことを確認する。イメージ図は以下の通り。

証明

下図を考える。

放物線Cを以下の式で定義する。

(1) $\begin{equation*} C: \: y_0(x) = a x^2 \end{equation*}$

任意の点(X, Y)における接線l₁の式は以下の様になる。

(2) $\begin{align*} l_1: \: y_1(x) &= y_1' (X) \cdot (x - X) + Y &= 2aX (x - X) + X^2 \end{align*}$

ここで、y₁‘は、図中の角θを用いて以下のように表せる。

(3) $\begin{equation*} y_1'(X) = \tan \theta \quad \left( -\frac{\pi}{2} \le \theta < \frac{\pi}{2} \right) \end{equation*}$

また、この点を通ってl₁に垂直な直線l₂の式は、この点におけるl2の微分係数をy₂‘として以下のように表せる。

(4) $\begin{equation*} l_2: \: y_2(x) = y_2' (X) \cdot (x - X) + Y \end{equation*}$

ここでy₂‘は、図中の角θを用いて以下のように導かれる。

(5) $\begin{align*} y_2'(X) &= - \tan \left( \dfrac{\pi}{2} - 2 \theta \right) \\ &= - \frac{\cos 2 \theta}{\sin 2 \theta} \\ &= - \frac{\cos^2 \theta - \sin^2 \theta}{2 \sin \theta \cos \theta} \\ &= - \frac{-1 + \tan^2 \theta}{2 \tan \theta} \end{align*}$

この式でθがπ/2よりも大きい場合でも、式形は変わらない。

ここで式(3)を考慮して、l₂の式は以下のように変形される。

(6) $\begin{equation*} y_2(x) = \frac{-1 + 4 a^2 X^2}{4aX} (x - X) + a X^2 \end{equation*}$

l₂がy軸と交わる点のy座標値を求める。

(7) $\begin{align*} y_2(0) &= \frac{-1 + 4 a^2 X^2}{4aX} (-X) + a X^2 \\ &= \frac{X - 4 a^2 X^3 + 4a^2 X^3}{4aX} \\ &= \frac{1}{4a} \end{align*}$

この値はXに寄らず一定なことから、y軸に平行な線が放物線で反射された線は、y軸上の1点を通る。

なお、入射線と反射線が直角になるときの入射線のx座標値は以下の通り。

(8) $\begin{align*} a x^2 = \frac{1}{4a} \quad \Leftrightarrow \quad x = \plusminus \frac{1}{2a} \end{align*}$

斜め入射について

たとえば先の図で、入射角が右側に傾いた場合を考える。

y軸の右側（xが正の側）からの入射線の放物線に対する角度は、y軸に平行な場合に対してより浅くなることから、反射方向はより下側に傾く。したがって、反射線とy軸の交点は下側に移動する。

一方y軸の左側（xが負の側）からの入射線の放物線に対する角度は、y軸に平行な場合に対してより深くなることから、反射方向はより上側に傾く。したがって、反射線とy軸の交点は上側に移動する。

少なくともy軸の両側で反射線のy軸との交点が一致しないことから、焦点は存在しない。より正確には、入射線のy軸に対する傾きをαなどと置いて上記のような計算をするとよい。

ロジスティック関数

2023-06-12 / tau / コメントする

増加率一定

個体の増加速度が個体数に比例する場合、以下のような方程式になる。

(1) $\begin{equation*} \frac{dN}{dt} =m N \end{equation*}$

この解は以下のような指数関数となり、ある程度以上から先は急激に個体が増加し、無限に増えていく。

(2) $\begin{equation*} N(t) = N_0 e^{mt} \end{equation*}$

ロジスティック関数～増加に対する歯止め

増加率を一定ではなく個体数Nに応じた値となるよう、以下の関数とする。

(3) $\begin{equation*} m(N) = r \left( 1 - \frac{N}{K} \right) \end{equation*}$

個体数が増えるにしたがって増加率は減少し、個体数がKのときに増加率はゼロ、それよりも多いときには個体数は減少する。

この増加率を適用した微分方程式は以下の通り。

(4) $\begin{equation*} \frac{dN}{dt} = r \left( 1 - \frac{N}{K} \right) N \end{equation*}$

まず以下のように変形。

(5) $\begin{equation*} \frac{dN}{dt} = \frac{r}{K} (K - N) N \end{equation*}$

変数分離形。

(6) $\begin{equation*} \frac{K}{(K - N) N} dN = r dt \end{equation*}$

分数部分を以下のように変形。

(7) $\begin{equation*} \left( \frac{1}{N} - \frac{1}{K - N} \right) dN = r dt \end{equation*}$

積分した一般解は以下の通り。

(8) $\begin{equation*} \ln N - \ln (K-N) = rt + const. \end{equation*}$

指数関数の形に。

(9) $\begin{equation*} \frac{N}{K - N} = A e^{rt} \end{equation*}$

Nをまとめる。

(10) $\begin{equation*} \frac{K - N}{N} = \frac{K}{N} - 1 = A e^{-rt} \end{equation*}$

Nについて解いた一般解を得る。

(11) $\begin{equation*} N = \frac{K}{1 + A e^{-rt}} \end{equation*}$

これにt=0のときの初期値N₀を適用して、以下の解を得る。

(12) $\begin{equation*} N = \frac{K}{ 1 + \left( \dfrac{K}{N_0} - 1 \right) e^{-rt} } \end{equation*}$

t=0のときは初期値N₀、t→∞のときはN=Kに収束する。

(13) $\begin{equation*} \left\{ \begin{array}{l} N(0) = N_0 \\ \lim\limits_{t \to \infty} N(t) = K \end{array} \end{equation*}$

N0=2, r=10, K=1000のグラフを描くと以下の通り。

また先の解を微分して増加速度の式を求めると以下の様になる。

パラメーターの影響

初期値N₀

初期値がKより小さいときはよく見られるロジスティック曲線でKに漸近する
Kと等しいときは変化しない
Kより大きいときは指数関数的にKに漸近する

増加率r

増加率が大きいほど立ち上がりが急になり、小さいほど緩やかになる。

収束値K

収束値Kに向かって漸近する。

増加速度

Nをtで微分して増加速度の式を得る。

(14) $\begin{equation*} \frac{dN}{dt} = r \frac{\left( \dfrac{K}{N_0} - 1 \right) e^{-rt}}{\left( 1 + \left( \dfrac{K}{N_0} - 1 \right) e^{-rt} \right)^2} \end{equation*}$

増加速度のグラフは以下の様になり、極大値を一つ持つ。

増加速度が最大となるtの値は、K/N₀ – 1 = Cとおいて以下の様に得られる。

(15) $\begin{equation*} t = \frac{1}{r} \ln C = \frac{1}{r} \ln \left( \frac{K}{N_0} - 1 \right) \end{equation*}$

これは以下の様にしても導ける。式(4)の値がゼロとなるのはN=K/2のときなので、これを式(12)に代入して、

(16) $\begin{equation*} 1 + \left( \dfrac{K}{N_0} - 1 \right) e^{-rt} = 2 \end{equation*}$

これを解いて(15)と同じ解を得る。

PythonCGI – 基本

2023-03-30 / tau / コメントする

概要

PythonのコードでCGI(Common Gateway Interface)によってHTMLをする方法の基本。

基本の枠組み

コード例

例えば以下の内容をindex.pyとして準備。

SheBangでPythonの場所を指定
Content-Typeを出力して1行空ける
出力内容を記述

#!/usr/bin/python3.6

print('Content-Type: text/html')
print('')
print('Python CGI Test')

#!/usr/bin/python3.6

print('Content-Type: text/html')

print('')

print('Python CGI Test')

HTTPのヘッダーで最低限Content-Typeを出力し、ボディーとの間に空行が1行必要。これがないと、500エラーとなり、ログには以下の様に記録される。

[cgi:error] [pid 30090] [client 192.168.33.1:65449] malformed header from script 'index.py': Bad header: Python CGI Test

1	[cgi:error] [pid 30090] [client 192.168.33.1:65449] malformed header from script 'index.py': Bad header: Python CGI Test

コードのモード確認

ファイルがrootの実行権限を持っていること。実行権限がない場合はchmod 755かchmod +xで設定する。

コードの配置

cgi実行用のディレクトリーにファイルを配置。Apacheの場合例えば/var/www/cgi-binなど。

ブラウザ表示

URLで[ホスト]/cgi-bin/index.pyを指定すると、ブラウザーにPython CGI Testと表示される。

HTML出力例

ASCII出力

基本の枠組みの出力に、以下の様にタグを加えると要素として表示される。

#!/usr/bin/python3.6

print('Content-Type: text/html')
print('')
print('<h1>Python CGI Test</h1>')
print('<p>Python CGI Test</p>')

#!/usr/bin/python3.6

print('Content-Type: text/html')

print('')

print('<h1>Python CGI Test</h1>')

print('<p>Python CGI Test</p>')

UTF-8出力

上のコードの一部を日本語にしてみる。

#!/usr/bin/python3.6

print('Content-Type: text/html')
print('')
print('<h1>Python CGI test</h1>')
print('<p>Python CGI テスト</p>')

#!/usr/bin/python3.6

print('Content-Type: text/html')

print('')

print('<h1>Python CGI test</h1>')

print('<p>Python CGI テスト</p>')

ところがこれをブラウザーで確認すると、h1要素は表示されるがp要素が全く表示されない。ソースを確認してもh1要素の行が表示されるだけ（このコードをコンソールで実行すると、h1要素の行もp要素の行も表示される）。

これを解決するには、ソースコードでio.TextIOWrapperを実行するとよいらしい。

#!/usr/bin/python3.6

import sys, io

sys.stdout = io.TextIOWrapper(sys.stdout.buffer, encoding='utf-8')

print('Content-Type: text/html')
print('')
print('<h1>Python CGI test</h1>')
print('<p>Python CGI テスト</p>')

#!/usr/bin/python3.6

import sys, io

sys.stdout = io.TextIOWrapper(sys.stdout.buffer, encoding='utf-8')

print('Content-Type: text/html')

print('')

print('<h1>Python CGI test</h1>')

print('<p>Python CGI テスト</p>')

上記の2行を追加すると、無事日本語まで表示された。

HTML出力

コンテンツを以下の様にHTMLの構造にして出力する。title要素も機能して、タブの表示が変更された。

#!/usr/bin/python3.6

import sys, io

sys.stdout = io.TextIOWrapper(sys.stdout.buffer, encoding='utf-8')

html = '''
<html>
    <head>
        <title>Python CGI</title>
    </head>
    <body>
        <h1>Python CGI test</h1>
        <p>Python CGI HTMLテスト</p>
    </body>
</html>
'''

print('Content-Type: text/html')
print('')
print(html)

#!/usr/bin/python3.6

import sys, io

sys.stdout = io.TextIOWrapper(sys.stdout.buffer, encoding='utf-8')

html = '''

<html>

<head>

<title>Python CGI</title>

</head>

<body>

<h1>Python CGI test</h1>

<p>Python CGI HTMLテスト</p>

</body>

</html>

'''

print('Content-Type: text/html')

print('')

print(html)

ループの利用例

以下のコードでは、見栄えは良くないがforループでli要素を生成している。

#!/usr/bin/python3.6

import sys, io

sys.stdout = io.TextIOWrapper(sys.stdout.buffer, encoding='utf-8')

html_head = '''
<head>
    <title>Python CGI</title>
</head>
'''

html_body = '''
<h1>Python CGI test</h1>
<p>Python CGI HTMLテスト</p>
'''

print('Content-Type: text/html')
print('')
print('<html>')
print(html_head)
print('<body>')
print(html_body)
print('<ol>')
for i in range(5):
    print('<li>{}番目のli要素</li>'.format(i + 1))
print('</ol>')
print('</body')
print('</html>')

#!/usr/bin/python3.6

import sys, io

sys.stdout = io.TextIOWrapper(sys.stdout.buffer, encoding='utf-8')

html_head = '''

<head>

<title>Python CGI</title>

</head>

'''

html_body = '''

<h1>Python CGI test</h1>

<p>Python CGI HTMLテスト</p>

'''

print('Content-Type: text/html')

print('')

print('<html>')

print(html_head)

print('<body>')

print(html_body)

print('<ol>')

for i in range(5):

print('<li>{}番目のli要素</li>'.format(i + 1))

print('</ol>')

print('</body')

print('</html>')

出力に以下が加わる。

1番目のli要素
2番目のli要素
3番目のli要素
4番目のli要素
5番目のli要素

Apacheの設定

今回は/etc/httpd/conf/httpd.confのデフォルトのままでcgi-scriptの設定を加えていないが、そのままで適切に実行された。

Atom – VagrantにSFTP接続

2023-03-26 / tau / コメントする

概要

RemoteFTPパッケージを利用
VagrantのSSHの設定内容を確認
Atomの.ftpconfigを編集
接続

VagrantのSSH設定内容確認

vagrant upの前の状態で、Vagrantfileのあるディレクトリー下でvagrant ssh-configを実行。

C:\vagrant\centos7>vagrant ssh-config
Host default
  HostName 127.0.0.1
  User vagrant
  Port 2222
  UserKnownHostsFile /dev/null
  StrictHostKeyChecking no
  PasswordAuthentication no
  IdentityFile C:/..../.vagrant.d/boxes/bento-VAGRANTSLASH-centos-7.7/0/virtualbox/vagrant_private_key
  IdentitiesOnly yes
  LogLevel FATAL

C:\vagrant\centos7>vagrant ssh-config

Host default

HostName 127.0.0.1

User vagrant

Port 2222

UserKnownHostsFile /dev/null

StrictHostKeyChecking no

PasswordAuthentication no

IdentityFile C:/..../.vagrant.d/boxes/bento-VAGRANTSLASH-centos-7.7/0/virtualbox/vagrant_private_key

IdentitiesOnly yes

LogLevel FATAL

.ftpconfigの編集

Atomを起動、Packages→RemoteFTP→ToggleでサイドパネルにRemoteタブを表示。Edit Configurationで.ftpconfigを表示させて編集。

{
    "protocol": "sftp",←SFTPを指定
    "host": "127.0.0.1",←ホスト名
    "port": 2222,←ポート番号
    "user": "vagrant",←SSH接続ユーザー名
    "pass": "*******",←SSH接続パスワード
    "promptForPass": false,
    "remote": "/home/vagrant/my_directory",←同期したいディレクトリー
    "local": "",
    "secure": false,
    "secureOptions": null,
    "connTimeout": 10000,
    "pasvTimeout": 10000,
    "keepalive": 10000,
    "watch": [],
    "watchTimeout": 500
}

{

"protocol": "sftp",←SFTPを指定

"host": "127.0.0.1",←ホスト名

"port": 2222,←ポート番号

"user": "vagrant",←SSH接続ユーザー名

"pass": "*******",←SSH接続パスワード

"promptForPass": false,

"remote": "/home/vagrant/my_directory",←同期したいディレクトリー

"local": "",

"secure": false,

"secureOptions": null,

"connTimeout": 10000,

"pasvTimeout": 10000,

"keepalive": 10000,

"watch": [],

"watchTimeout": 500

}

接続開始と終了

サイドパネルのConnectを実行して接続。終了時はPackages→RemoteFTP→Disconnect。

コイル（インダクター）

2023-02-28 / tau / コメントする

電流・磁界の法則

右ネジの法則

電流が流れると、その方向に対して右回りの磁界が発生する（Maxwell’s right-handed screw rule）。

右手の法則

コイルに電流を流すと、電流の向きが右手を握った各指の方向のとき親指の挿す方向に磁界が発生する。

フレミングの左手／右手の法則

絵は面倒なので割愛。人差し指が磁界、中指が電流、親指が力の方向。左手は磁界内の電流に働く力、右手は磁界内で運動する場合に発生する電流の方向。

ローレンツ力

電荷e[C]の荷電粒子が磁束密度B[T]内を運動ベクトルvで移動するとき、荷電粒子に対してフレミングの左手の法則に従って力が働く。

このとき、vが磁束に対してなす角をθとすると、荷電粒子に働く力は以下の様になる。

(1) $\begin{equation*} f = q v (\sin \theta) B \end{equation*}$

ローレンツ力の方向まで含める場合、ベクトルの外積よって以下の様に表せる。

(2) $\begin{equation*} \boldsymbol{f} = q \boldsymbol{v} \times \boldsymbol{B} \end{equation*}$

レンツの法則

コイルを通る磁束が変化するとき、その磁束の変化を妨げる方向に誘導電流が生じる。

たとえば以下の図では、コイルに対して磁石のN極側を近づけている。このときコイルに対して左から右へ向かう磁束が増加するので、それ打ち消す右から左の磁束を増やすように誘導電流が流れる。

この状態で磁石が離れていくときは右向きの磁束が減少するので、コイル内で同じ右向きの磁束を発生させるよう、上図と逆向きの電流が流れる。

一方、S極が近づくときは左向きの磁束が増えるので、これと逆の右向きの磁束が発生するよう、上図と逆向きの電流が流れる。

S極が離れる場合には、左向きの磁束が減少するので、これを補うように左向きの磁束を発生させる方向（上図と同じ方向）に電流が流れる。

ファラデーの法則

閉回路を貫く磁束Φが変化するとき、レンツの法則によりその変化を妨げる方向の電流が流れるが、この起電力を誘導起電力という。誘導起電力の大きさは以下のように表される。

(3) $\begin{equation*} | V | = \left| \frac{d \Phi}{dt} \right| \end{equation*}$

起電力の正負の向きについて、「磁束の変化を妨げるように」というレンツの法則から、以下の様に表現される。

(4) $\begin{equation*} V = - \frac{d \Phi}{dt} \end{equation*}$

またコイルの巻き数がNのときは、以下の様になる。

(5) $\begin{equation*} V = - N \frac{d \Phi}{dt} \end{equation*}$

コイルの自己誘導

自己誘導とは

コイルにかかる電圧が変化した場合場合、電流の変化に応じて磁界が変化するが、レンツの法則によってそれを阻止しようとする方向の電流を流そうという起電力も生じる。このような現象をコイルの自己誘導と言い、自己誘導によって生じる元の電圧と逆の起電力を逆起電力という。

電源が立ち上がった場合

たとえば以下のような回路を考える。ここで電源電圧が0→Eに立ち上がった場合、コイルによる逆起電力、抵抗による電圧降下が生じる。電源の起電力は正極側を⊕としている。抵抗Rの電圧は電源に対して電圧降下となる電流の向きの矢印、コイルの方は電流の変化によるので両方向きの矢印としている。

電流をI = I(t)として、電圧のバランスを定式化すると、以下のようになる。

(6) $\begin{equation*} E - L \frac{dI}{dt} - RI = 0 \end{equation*}$

この微分方程式を以下のように解いていく。

(7) $\begin{equation*} \frac{dI}{E - RI} = \frac{dt}{L} \end{equation*}$

(8) $\begin{equation*} -\frac{1}{R} \ln (E - RI) = \frac{t}{L} + const \end{equation*}$

(9) $\begin{equation*} I = \frac{E - k e^{- \frac{R}{L} t}}{R} \end{equation*}$

ここでI_t=0 = 0の条件によりkを決定する。

(10) $\begin{equation*} \frac{E - k}{R} = 0 \quad \Rightarrow \quad k = E \end{equation*}$

よって、自己誘導を含めた電流変化は以下のように求められる。

(11) $\begin{equation*} I = \frac{E}{R} \left(1 - e^{- \frac{R}{L} t} \right) \end{equation*}$

以下のグラフは、L = 100mH、R = 1kΩ、E = 5Vの場合にスイッチON以降の電流変化を計算したもの。自己誘導の影響がなくなり定常電圧になるのに500μsほどかかっている。

電圧が立ち下がった場合

初期電流I_t=0 = E/Rとして、t = 0でE = 0になったとして先の微分方程式を解いてみる。まず式(6)でE = 0と置く

(12) $\begin{equation*} - L \frac{dI}{dt} - RI = 0 \end{equation*}$

これを解いて

(13) $\begin{equation*} I = k e^{- \frac{R}{L} t} \end{equation*}$

初期条件を考慮して以下を得る。

(14) $\begin{equation*} I = \frac{E}{R} e^{- \frac{R}{L} t} \end{equation*}$

この式形は式(11)と上下逆の形になっていて、以下のようなグラフになる。

サージ

サージの考え方？

コイルを含む回路を半導体素子で開閉した場合、スイッチOFFの際に高電圧のサージが発生するということを知った。ただし定性的な（あるいは感覚的な）原理は多くみられるが、そのメカニズムがどうも腹に落ちない。

「スイッチOFFにしても電流が流れようとするので誘導起電力が発生し・・・」という説明を見かけるが、もし理想的なスイッチで瞬間的にOFFとなるなら、誘導電流が流れる時間がゼロだから、回路としてはそのまま黙ってしまうのではないか（dI/dtが無限大になるのとどう関係するのか定かではないが）。

スイッチが完全にOFFになるまでに若干のスパークが発生することや、スイッチング阻止の抵抗が無限大ではないことを含めて説明している場合もあり、これは現実論として納得できる。

特にこちらのサイトはとても参考になったので、これを自分なりにトレースして、理解を試みた。

まず以下の図で、電源Eに接続していた状態からスイッチを抵抗S側に切り替えたとする。ただし以下の点に留意する。

切り替え前は定常状態で、回路の電流はI = E/R
ここでのスイッチは理想的なスイッチとし、抵抗Sが現実のスイッチ切り替え時の抵抗に相当

ここで切り替えの瞬間をt = 0として微分方程式は以下のようになる。

(15) $\begin{equation*} - L \frac{dI}{dt} - RI - SI = 0 \end{equation*}$

初期条件t = 0でI = E/Rとして解いて、以下を得る。

(16) $\begin{equation*} I = \frac{E}{R} e^{- \frac{R + S}{L}t} \end{equation*}$

この電流に対してコイルは起電側となり、2つの抵抗で電圧降下となって、それらは以下のようになる。

(17) $\begin{equation*} \left\{ \begin{array}{l} V_R = RI = E e^{- \frac{R + S}{L}t} \\ V_S = SI = \dfrac{S}{R} E e^{- \frac{R + S}{L}t} \\ V_L = - L \dfrac{dI}{dt} = - \dfrac{R + S}{R} E e^{- \frac{R + S}{L}t} \end{array} \end{equation*}$

この式によるなら、t=0でコイルによる起電力は(R + S)/Rとなり、このうちS/Rが抵抗Sの電圧降下となる。たとえばR=1kΩのときにSが10kΩでも元の電源電圧の10倍の電圧がSの両端にかかることになる。

この様子を先と同じ条件L = 100mH、R = 1kΩ、E = 5Vに加えてS = 10kΩとして描いたのが以下のグラフ。スイッチOFFのときにEの10倍の50Vが生じ、そこから急激に電圧が下がっている。また時定数(R + S)/Rも大きくなるので、減少の時間も1オーダー短くなっている。

このSが大きくなると、その倍率に応じて大きな電圧が生じ、低減時間は短くなる。すなわち、一瞬の間だけ高電圧が発生する。これがコイルによるサージと呼ばれるものではないか。

ただし元々接続されていたRの両端の電圧の最大値は変わらないので、サージの影響を受けるのはスイッチ素子ということになる。ここにトランジスターなどを使っていると、たとえばC–E間に逆向きの高電圧がかかって破壊されてしまう。

保護回路

コイルサージから回路を保護するためにいろいろあるようだが、最も簡単なのは以下の様にダイオードを加えることらしい。

通常のスイッチONの状態ではダイオードが逆向きなのでコイルに電流が流れ、サージ電流はダイオードを通じて戻るので、RやSには影響を与えない。

Raspberry Pi – ブザー

2023-02-25 / tau / コメントする

概要

Raspberry Pi用キットのアクティブ・ブザー、パッシブ・ブザーの実験。

アクティブ・ブザー

単純接続

アクティブ・ブザーは振動源を内蔵していて、電流が流すだけで音が出る。まず、単純に3.3Vの電源に繋いでみた。

抵抗なしで直接GNDに繋ぐと、「ピュー」という音が鳴る。抵抗値が10Ωで音はかなり小さくなり、100Ωにするとかすかに聞こえるくらいの音になった。

回路図

ブザーを電源に直接GPIOに繋いでもRasberry Piで制御できるが、キットの回路図はPNP型のトランジスターを介して接続していた。GPIOから流れる電流をより少なくするためと思われる。

この回路の場合、GPIOをHIGHにすると音はならず、LOWにするとC-E間にも電流が流れて音が出る。音量は直接3.3Vに繋いだ時と同じ。

コード

以下のコードでは単純にGPIOのHIGH/LOWを切り替えて、一定間隔でブザーを鳴らす。周期を短くすると「ピュピュピュピュ・・・」と連続して鳴動する。

import RPi.GPIO as GPIO
import time

# Define GPIO17 pin
PIN = 17

# Setup GPIO mode and pin
GPIO.setmode(GPIO.BCM)
GPIO.setup(PIN, GPIO.OUT, initial=GPIO.HIGH)

# Function to end
def destroy():
    GPIO.output(PIN, GPIO.HIGH)
    GPIO.cleanup()

try:
    # Repeat buzzing
    while True:
        GPIO.output(PIN, GPIO.LOW)
        time.sleep(0.1)
        GPIO.output(PIN, GPIO.HIGH)
        time.sleep(0.1)
# Quit when CTRL+C pressed
except KeyboardInterrupt:
    destroy()

import RPi.GPIO as GPIO

import time

# Define GPIO17 pin

PIN = 17

# Setup GPIO mode and pin

GPIO.setmode(GPIO.BCM)

GPIO.setup(PIN, GPIO.OUT, initial=GPIO.HIGH)

# Function to end

def destroy():

GPIO.output(PIN, GPIO.HIGH)

GPIO.cleanup()

try:

# Repeat buzzing

while True:

GPIO.output(PIN, GPIO.LOW)

time.sleep(0.1)

GPIO.output(PIN, GPIO.HIGH)

time.sleep(0.1)

# Quit when CTRL+C pressed

except KeyboardInterrupt:

destroy()

パッシブ・ブザー

ソフトウェアによる音

パッシブブザーは入力の1パルスに対して1回だけクリック音が出る。アクティブ・ブザーと同じ回路図でブザーをパッシブブザーに取り換えて同じコードで実行すると”click, click, …”と単調な音が続く。

ここで入力をある周波数にすると、その周波数に対応した音程のビープ音になる。

以下のコードは440Hzの音を鳴らすもので、設定した周波数の周期で矩形パルスを発生させてAの音を出す。ソフトウェア制御なので、ときどき音が途切れたりする。

import RPi.GPIO as GPIO
import time

# Define GPIO17 pin
PIN = 17

# Setup GPIO mode and pin
GPIO.setmode(GPIO.BCM)
GPIO.setup(PIN, GPIO.OUT, initial=GPIO.HIGH)

def tone(freq):
    cycle_time = 1 / freq / 2
    while True:
        GPIO.output(PIN, GPIO.LOW)
        time.sleep(cycle_time)
        GPIO.output(PIN, GPIO.HIGH)
        time.sleep(cycle_time)

# Function to end
def destroy():
    GPIO.output(PIN, GPIO.HIGH)
    GPIO.cleanup()

try:
    # Make a tone
    tone(440)
# Quit when CTRL+C pressed
except KeyboardInterrupt:
    destroy()

import RPi.GPIO as GPIO

import time

# Define GPIO17 pin

PIN = 17

# Setup GPIO mode and pin

GPIO.setmode(GPIO.BCM)

GPIO.setup(PIN, GPIO.OUT, initial=GPIO.HIGH)

def tone(freq):

cycle_time = 1 / freq / 2

while True:

GPIO.output(PIN, GPIO.LOW)

time.sleep(cycle_time)

GPIO.output(PIN, GPIO.HIGH)

time.sleep(cycle_time)

# Function to end

def destroy():

GPIO.output(PIN, GPIO.HIGH)

GPIO.cleanup()

try:

# Make a tone

tone(440)

# Quit when CTRL+C pressed

except KeyboardInterrupt:

destroy()

PWMによる音

上と同様のことを、ハードウェアのPWMで実装したのが下記のコード。

ハードウェアPWMのGPIO13にピンを変えて、周波数やデューティー・サイクルを指定してAの音を2秒間出している。

import RPi.GPIO as GPIO
import time

# Define GPIO17 pin
PWM_PIN = 13

# Setup GPIO mode and pin
GPIO.setmode(GPIO.BCM)
GPIO.setup(PWM_PIN, GPIO.OUT)
FREQ = 440
PWM = GPIO.PWM(PWM_PIN, FREQ)

# Make a tone
PWM.start(50)
time.sleep(2)

# Ending process
PWM.ChangeDutyCycle(0)
GPIO.cleanup()

import RPi.GPIO as GPIO

import time

# Define GPIO17 pin

PWM_PIN = 13

# Setup GPIO mode and pin

GPIO.setmode(GPIO.BCM)

GPIO.setup(PWM_PIN, GPIO.OUT)

FREQ = 440

PWM = GPIO.PWM(PWM_PIN, FREQ)

# Make a tone

PWM.start(50)

time.sleep(2)

# Ending process

PWM.ChangeDutyCycle(0)

GPIO.cleanup()

音階

PWMを使ってスケールを鳴らしてみた。

辞書定数で各音階に対応する周波数をセットして、ある周波数の1音を鳴らすクラスを定義。Cのスケールで音階を鳴らしている。

import RPi.GPIO as GPIO
import time

# Define GPIO17 pin
PWM_PIN = 13

# Setup GPIO mode and pin
GPIO.setmode(GPIO.BCM)
GPIO.setup(PWM_PIN, GPIO.OUT)
# Define tones and frequencies of scale
TONES = {
    'c4': 261.626,
    'd4': 293.655,
    'e4': 329.628,
    'f4': 349.228,
    'g4': 391.995,
    'a4': 440.000,
    'h4': 493.883,
    'c5': 523.251,
}

# Class to beep a tone
class Tone:
    # Initialize an instance by specifying PWM pin number
    def __init__(self, pwm_pin):
        self.pwm = GPIO.PWM(pwm_pin, 1)

    # Beep a tone by specifying frequency and duration
    def beep(self, freq, duration):
        self.pwm.ChangeFrequency(freq)
        self.pwm.ChangeDutyCycle(0.5)
        self.pwm.start(50)
        time.sleep(duration)

    def none(self, duration):
        self.pwm.ChangeDutyCycle(0)
        time.sleep(duration)
                                 
    # Destroy instance by cleaning up pins
    def destroy(self):
        self.pwm.ChangeDutyCycle(0)
        GPIO.cleanup()

tone = Tone(PWM_PIN)
tone.beep(TONES['c4'], 0.3)
tone.none(0.3)
tone.beep(TONES['d4'], 0.3)
tone.beep(TONES['e4'], 0.3)
tone.beep(TONES['f4'], 0.3)
tone.beep(TONES['g4'], 0.3)
tone.beep(TONES['a4'], 0.3)
tone.beep(TONES['h4'], 0.3)
tone.beep(TONES['c5'], 0.3)
tone.none(0.3)
tone.beep(TONES['h4'], 0.3)
tone.beep(TONES['a4'], 0.3)
tone.beep(TONES['g4'], 0.3)
tone.beep(TONES['f4'], 0.3)
tone.beep(TONES['e4'], 0.3)
tone.beep(TONES['d4'], 0.3)
tone.beep(TONES['c4'], 0.3)
tone.destroy()

import RPi.GPIO as GPIO

import time

# Define GPIO17 pin

PWM_PIN = 13

# Setup GPIO mode and pin

GPIO.setmode(GPIO.BCM)

GPIO.setup(PWM_PIN, GPIO.OUT)

# Define tones and frequencies of scale

TONES = {

'c4': 261.626,

'd4': 293.655,

'e4': 329.628,

'f4': 349.228,

'g4': 391.995,

'a4': 440.000,

'h4': 493.883,

'c5': 523.251,

}

# Class to beep a tone

class Tone:

# Initialize an instance by specifying PWM pin number

def __init__(self, pwm_pin):

self.pwm = GPIO.PWM(pwm_pin, 1)

# Beep a tone by specifying frequency and duration

def beep(self, freq, duration):

self.pwm.ChangeFrequency(freq)

self.pwm.ChangeDutyCycle(0.5)

self.pwm.start(50)

time.sleep(duration)

def none(self, duration):

self.pwm.ChangeDutyCycle(0)

time.sleep(duration)

# Destroy instance by cleaning up pins

def destroy(self):

self.pwm.ChangeDutyCycle(0)

GPIO.cleanup()

tone = Tone(PWM_PIN)

tone.beep(TONES['c4'], 0.3)

tone.none(0.3)

tone.beep(TONES['d4'], 0.3)

tone.beep(TONES['e4'], 0.3)

tone.beep(TONES['f4'], 0.3)

tone.beep(TONES['g4'], 0.3)

tone.beep(TONES['a4'], 0.3)

tone.beep(TONES['h4'], 0.3)

tone.beep(TONES['c5'], 0.3)

tone.none(0.3)

tone.beep(TONES['h4'], 0.3)

tone.beep(TONES['a4'], 0.3)

tone.beep(TONES['g4'], 0.3)

tone.beep(TONES['f4'], 0.3)

tone.beep(TONES['e4'], 0.3)

tone.beep(TONES['d4'], 0.3)

tone.beep(TONES['c4'], 0.3)

tone.destroy()

音楽

改めて音符・給付を並べて音楽を演奏するクラスを定義。ついでにテンポも指定できるようにした。

このクラスを使って、D-durの音階を鳴らしている。

import RPi.GPIO as GPIO
import time

# Define GPIO17 pin
PWM_PIN = 13

# Setup GPIO mode and pin
GPIO.setmode(GPIO.BCM)
GPIO.setup(PWM_PIN, GPIO.OUT)
# Define tones and frequencies of scale

# Class to play music
class Music:
    # Class constant of tones and frequencies
    TONES = {
        'g3': 195.998, 'gis3': 207.652,
        'a3': 220.000, 'ais3': 233.082,
        'h3': 246.942,
        'c4': 261.626, 'cis4': 277.183,
        'd4': 293.655, 'dis4': 311.127,
        'e4': 329.628,
        'f4': 349.228, 'fis4': 369.994,
        'g4': 391.995, 'gis4': 415.305,
        'a4': 440.000, 'ais4': 466.164,
        'h4': 493.883,
        'c5': 523.251, 'cis5': 554.365,
        'd5': 587.330, 'dis5': 622.254,
        'e5': 659.255,
        'f5': 698.456, 'fis5': 739.989,
        'g5': 783.991, 'gis5': 830.609,
    }
    # Class constant of tempos
    TEMPOS = {
        'Largo': 46,
        'Adagio': 56,
        'Andante': 72,
        'Moderato': 96,
        'Allegro': 132,
        'Vivace': 160,
        'Presto': 184,
    }

    # Initialize an instance by specifying PWM pin number
    def __init__(self, pwm_pin):
        self.pwm = GPIO.PWM(pwm_pin, 1)
        self.tempo = self.TEMPOS['Moderato']

    def _beat_to_duration(self, beat):
        return 60 / self.tempo * 4 / beat

    # Beep a tone by specifying frequency and duration
    def _beep(self, freq, duration):
        self.pwm.ChangeFrequency(freq)
        self.pwm.ChangeDutyCycle(0.5)
        self.pwm.start(50)
        time.sleep(duration)

    # Set new tempo
    def set_tempo(self, tempo):
        self.tempo = tempo

    # Make a sound of note
    # beat: 1, 2, 4, 8, 16, 32: whole, half, quarter, eighth, sixteenth, thirty-second
    def note(self, beat, pitch):
        freq = self.TONES[pitch]
        duration = self._beat_to_duration(beat)
        self._beep(freq, duration)

    # Rest of beat length
    def rest(self, beat):
        duration = self._beat_to_duration(beat)
        self.pwm.ChangeDutyCycle(0)
        time.sleep(duration)
                                 
    # Destroy instance by cleaning up pins
    def destroy(self):
        self.pwm.ChangeDutyCycle(0)
        GPIO.cleanup()

m = Music(PWM_PIN)
m.set_tempo(Music.TEMPOS['Allegro'])

m.note(4, 'd4')
m.rest(4)
m.note(4, 'e4')
m.note(4, 'fis4')
m.note(4, 'g4')
m.note(4, 'a4')
m.note(4, 'h4')
m.note(4, 'cis5')
m.note(4, 'd5')
m.rest(4)
m.note(4, 'cis5')
m.note(4, 'h4')
m.note(4, 'a4')
m.note(4, 'g4')
m.note(4, 'fis4')
m.note(4, 'e4')
m.note(2, 'd4')

m.destroy()

100

101

import RPi.GPIO as GPIO

import time

# Define GPIO17 pin

PWM_PIN = 13

# Setup GPIO mode and pin

GPIO.setmode(GPIO.BCM)

GPIO.setup(PWM_PIN, GPIO.OUT)

# Define tones and frequencies of scale

# Class to play music

class Music:

# Class constant of tones and frequencies

TONES = {

'g3': 195.998, 'gis3': 207.652,

'a3': 220.000, 'ais3': 233.082,

'h3': 246.942,

'c4': 261.626, 'cis4': 277.183,

'd4': 293.655, 'dis4': 311.127,

'e4': 329.628,

'f4': 349.228, 'fis4': 369.994,

'g4': 391.995, 'gis4': 415.305,

'a4': 440.000, 'ais4': 466.164,

'h4': 493.883,

'c5': 523.251, 'cis5': 554.365,

'd5': 587.330, 'dis5': 622.254,

'e5': 659.255,

'f5': 698.456, 'fis5': 739.989,

'g5': 783.991, 'gis5': 830.609,

}

# Class constant of tempos

TEMPOS = {

'Largo': 46,

'Adagio': 56,

'Andante': 72,

'Moderato': 96,

'Allegro': 132,

'Vivace': 160,

'Presto': 184,

}

# Initialize an instance by specifying PWM pin number

def __init__(self, pwm_pin):

self.pwm = GPIO.PWM(pwm_pin, 1)

self.tempo = self.TEMPOS['Moderato']

def _beat_to_duration(self, beat):

return 60 / self.tempo * 4 / beat

# Beep a tone by specifying frequency and duration

def _beep(self, freq, duration):

self.pwm.ChangeFrequency(freq)

self.pwm.ChangeDutyCycle(0.5)

self.pwm.start(50)

time.sleep(duration)

# Set new tempo

def set_tempo(self, tempo):

self.tempo = tempo

# Make a sound of note

# beat: 1, 2, 4, 8, 16, 32: whole, half, quarter, eighth, sixteenth, thirty-second

def note(self, beat, pitch):

freq = self.TONES[pitch]

duration = self._beat_to_duration(beat)

self._beep(freq, duration)

# Rest of beat length

def rest(self, beat):

duration = self._beat_to_duration(beat)

self.pwm.ChangeDutyCycle(0)

time.sleep(duration)

# Destroy instance by cleaning up pins

def destroy(self):

self.pwm.ChangeDutyCycle(0)

GPIO.cleanup()

m = Music(PWM_PIN)

m.set_tempo(Music.TEMPOS['Allegro'])

m.note(4, 'd4')

m.rest(4)

m.note(4, 'e4')

m.note(4, 'fis4')

m.note(4, 'g4')

m.note(4, 'a4')

m.note(4, 'h4')

m.note(4, 'cis5')

m.note(4, 'd5')

m.rest(4)

m.note(4, 'cis5')

m.note(4, 'h4')

m.note(4, 'a4')

m.note(4, 'g4')

m.note(4, 'fis4')

m.note(4, 'e4')

m.note(2, 'd4')

m.destroy()

トランジスター

2023-02-23 / tau / コメントする

バイポーラトランジスター

バイポーラ(bipolar)は「二極の」という意味で、バイポーラトランジスターはP型・N型の2つの半導体、電子(electron)と正孔(hole)の2つが対をなして機能する。

PNP型トランジスター

PNP型トランジスターの原理は以下の通りで、正孔を持つP型半導体でごく薄いN型の半導体を挟んでいる。

エミッター～コレクター間に正電圧をかけても、それぞれの正孔がベースの電子と結合して空乏層(deplation layer)が生じ、電流は流れない。

ここでエミッター～ベース間に正電圧をかけると、それぞれの間の成功と電子は結合するが、ベースが非常に薄いためエミッターの正孔が通り抜けてコレクターに達し、電流が流れる。

回路図の表現は以下の通りで、コレクター・ベースに対してにエミッターに正電圧をかける。

たとえばエミッター側に負荷素子を繋ぎ、エミッター電圧をかける。ベース側の電流のON/OFFによってE-C間の電流が流れ、I_Bに比べて大きなI_Eのスイッチングや増幅が可能になる。

S8550トランジスター

S8550はFairchild社のSS8550の中国製らしい。PNP型のトランジスターで、以下の特徴を持つ。

低圧、大電流タイプのPNPトランジスター
To-92パッケージ
連続最大コレクター電流：500mA
CE間電圧：VCEO = –25V
CB間電圧：VCBO = –40V
EB間電圧：VBEO = –5V
電流増幅率：hFE = 85～300

ピン配置は以下の通り。

Raspberry Pi – I2C～LCD1602

2023-02-19 / tau / コメントする

概要

ここではI2C接続によるLCD1602の制御について整理する。

Raspberry Pi用のキットにはI2CがセットされたLCD1602が同梱されていたが、Pythonのモジュールが見つからなかった。ゼロから組み立てようかとCのコードを読んでみたが、いま一つわからない。そこでネット上をいろいろと探して、自分なりに理解してみた。

LCD1602

LCD1602のピン配置

LCD1602のピン配置は以下の様になっているらしい。上から順番に1～16。

各ピンの意味は以下の通り。

GND	Ground
+5V	Vcc（電源）
CNT	L→H→LでDB0～DB7ピンと信号伝送
RS	Register Select -> H: Data, L: Command
R/W	H: Read, L: Write
E	L→H→LでDB0～DB7ピンと信号伝送
DB0～DB7	8ビットデータ
A	LEDのアノード
K	LEDのカソード

表示領域～DDRAM

2行表示の場合のDDRAMアドレスの割り当ては以下の様になっている。

LCD1602のコマンド

LCD1602のコマンドは以下の通り。H→1、L→0で表している。

RS=0のときはコマンド、RS=1のときはデータを表す
R/W＝1で読み出し、R/W=0で書き込みで、コマンドは常にR/W=0
コマンドの場合は8ビットのDB7～0で最初に1が現れたビットによってコマンドが変わる
書き込み/読み出しは、EをL→H→Lと変化させて実行

8ビット/4ビットモードの設定

LCD1602起動時、確実に8ビット/4ビットモードをセットする手順は以下の通り。

起動直後の初期設定では、適切な待機時間を挟んで4ビットで0x3を3回書き込んだ後に0x2を書き込むことで4ビットモードに設定される。

I2CによるLCD1602の制御

接続

キットのLCD1602にはあらかじめI2C接続のためのボードが接続されていた。チップはHLF8574Tと書かれていたが、これは中国製らしくフィリップス製のPCF8574と同じ機能らしい。PCF8574はI2C I/Oエクスパンダ―というチップで、I2Cに準拠しSDAを介したシリアルの通信と、P0～P7の8ビットパラレルの通信を変換する。

PCF8574のP0～P7が8ビットのレジスターの各ビットに相当し、それらはLCD1602の各ピンと以下のように接続されている（他のピンは省略している）。

参考サイト：

Raspberry Pi Python I2C LCD1602表示テスト

PCF8574	LCD1602	LCD1602の機能
P7	DB7	4ビットデータのbit3
P6	DB6	4ビットデータのbit2
P5	DB5	4ビットデータのbit1
P4	DB4	4ビットデータのbit0
P3	K	バックライトのカソード
P2	E	L→H→LでDB0～DB7ピンと信号伝送
P1	R/W	H: Read, L: Write
P0	RS	Register Select -> H: Data, L: Command

DB0～DB3は接続されていないことから、このモジュールは常に4ビットモードで使用する必要がある。

P2に接続されたKピンはバックライトのカソードにあたり、トランジスターのC~Bを介してGNDに接続されている。

LCDとRaspiの接続

Rasberey PiのGPIO2と3（3番ピンと5番ピン）がSDAとSCLに対応しており、電源・GNDとともにこれらをLCDの端子（正確にはLCDに接続されたエキスパンダーの端子）に接続する。

SDAとSCLに対するプルアップ抵抗がないが、LCD/I2C内部でプルアップされているらしい。

初期手順

Raspberry Piの手順に従ってI2Cを有効化した後、デバイスアドレスを確認（I2Cを参照）。ここでは、LCD1602のデバイスアドレスは0x27。

$ i2cdetect -y 1
     0  1  2  3  4  5  6  7  8  9  a  b  c  d  e  f
00:          -- -- -- -- -- -- -- -- -- -- -- -- -- 
10: -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- 
20: -- -- -- -- -- -- -- 27 -- -- -- -- -- -- -- -- 
30: -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- 
40: -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- 
50: -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- 
60: -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- 
70: -- -- -- -- -- -- -- --

$ i2cdetect -y 1

0 1 2 3 4 5 6 7 8 9 a b c d e f

00: -- -- -- -- -- -- -- -- -- -- -- -- --

10: -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- --

20: -- -- -- -- -- -- -- 27 -- -- -- -- -- -- -- --

30: -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- --

40: -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- --

50: -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- --

60: -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- --

70: -- -- -- -- -- -- -- --

コード

動作テスト

LCDモジュールを4ビットモードにセット後、画面をクリアしてカーソルをブリンクさせる。

import smbus2 as smbus
import time

# Set constants
BUS = smbus.SMBus(1)
LCD_ADDR = 0x27
TW = 0.001 # pulse with for enable

# Write 4bits
def write_4bits(bits):
    buf = bits << 4
    # 0xC: BL=1, E=1, R/W=0, RS=0
    BUS.write_byte(LCD_ADDR, buf | 0x0C)
    time.sleep(TW)
    # 0xFB: 1011 -> only E=0
    BUS.write_byte(LCD_ADDR, buf & 0xFB)

# Write one byte command by dividing higher and lower 4bits
def write_command(command):
    # Write higher bits
    buf = command & 0xF0 | 0x0C
    BUS.write_byte(LCD_ADDR, buf)
    time.sleep(TW)
    BUS.write_byte(LCD_ADDR, buf & 0xFB)
    # Write lower bits    
    buf = (command << 4) | 0x0C
    BUS.write_byte(LCD_ADDR, buf)
    time.sleep(TW)
    BUS.write_byte(LCD_ADDR, buf & 0xFB)

# Set 8bit mode initially
write_4bits(0x3)
time.sleep(0.005)
write_4bits(0x3)
time.sleep(0.001)
write_4bits(0x3)
# Set 4bit mode
write_4bits(0x2)

# Commands
# Function set: 001(DL)|NFxx
# DL=0(4bit mode)
# N=1(2 lines)
# F=0(5x8 font)
write_command(0x28)
time.sleep(0.002)
# Display ON/OFF: 0000|1DCB
# D=1(display ON)
# C=1(Cursor ON)
# B=1(Blink ON)
write_command(0x0F)
time.sleep(0.002)
# Clear Display: 0000|0001
write_command(0x01)
time.sleep(0.002)

import smbus2 as smbus

import time

# Set constants

BUS = smbus.SMBus(1)

LCD_ADDR = 0x27

TW = 0.001 # pulse with for enable

# Write 4bits

def write_4bits(bits):

buf = bits << 4

# 0xC: BL=1, E=1, R/W=0, RS=0

BUS.write_byte(LCD_ADDR, buf | 0x0C)

time.sleep(TW)

# 0xFB: 1011 -> only E=0

BUS.write_byte(LCD_ADDR, buf & 0xFB)

# Write one byte command by dividing higher and lower 4bits

def write_command(command):

# Write higher bits

buf = command & 0xF0 | 0x0C

BUS.write_byte(LCD_ADDR, buf)

time.sleep(TW)

BUS.write_byte(LCD_ADDR, buf & 0xFB)

# Write lower bits

buf = (command << 4) | 0x0C

BUS.write_byte(LCD_ADDR, buf)

time.sleep(TW)

BUS.write_byte(LCD_ADDR, buf & 0xFB)

# Set 8bit mode initially

write_4bits(0x3)

time.sleep(0.005)

write_4bits(0x3)

time.sleep(0.001)

write_4bits(0x3)

# Set 4bit mode

write_4bits(0x2)

# Commands

# Function set: 001(DL)|NFxx

# DL=0(4bit mode)

# N=1(2 lines)

# F=0(5x8 font)

write_command(0x28)

time.sleep(0.002)

# Display ON/OFF: 0000|1DCB

# D=1(display ON)

# C=1(Cursor ON)

# B=1(Blink ON)

write_command(0x0F)

time.sleep(0.002)

# Clear Display: 0000|0001

write_command(0x01)

time.sleep(0.002)

冒頭で定数を定義している。TWはEを1にしてからLに戻すまでの待機時間で、データシートでは最小230nsという値もあったが、Pythonのtime.sleepの分解能もあり、1ms（以上）としている。

# Set constants
BUS = smbus.SMBus(1)
LCD_ADDR = 0x27
TW = 0.001 # pulse with for enable

# Set constants

BUS = smbus.SMBus(1)

LCD_ADDR = 0x27

TW = 0.001 # pulse with for enable

次に、4ビットのデータを書き込む関数を定義している。

引数のデータの下位4ビットを取り出し、4ビットシフトして上位4ビットへ
下位4ビットにコマンドセット
- バックライトON、転送Enable、Writeモード、コマンドレジスターに書き込み指示
書き込みウェイト
EnableをLowにして書き込み

# Write 4bits
def write_4bits(bits):
    buf = (bits & 0xF) << 4
    # 0xC: BL=1, E=1, R/W=0, RS=0
    BUS.write_byte(LCD_ADDR, buf | 0x0C)
    time.sleep(TW)
    # 0xFB: 1011 -> only E=0
    BUS.write_byte(LCD_ADDR, buf & 0xFB)

# Write 4bits

def write_4bits(bits):

buf = (bits & 0xF) << 4

# 0xC: BL=1, E=1, R/W=0, RS=0

BUS.write_byte(LCD_ADDR, buf | 0x0C)

time.sleep(TW)

# 0xFB: 1011 -> only E=0

BUS.write_byte(LCD_ADDR, buf & 0xFB)

もう1つの関数は、1バイトのコマンドをLCDに書き込む。4ビットモードなので上位・下位の4ビットに分けて書き込んでいる。

コマンド送信の場合の手順は、上位4ビットの場合は0xF0でマスク、下位4ビットの場合は0xFでマスクして4ビット分シフトした後、以下の通り。

下位4ビットはコマンド書き込みイネーブルで、KE(RW)(RS)=0b1100=0xC
TWの間ウェイト
その後Eのみ0とするため0b11111011=0xFBでマスクして書き込み

# Write one byte command by dividing higher and lower 4bits
def write_command(command):
    # Write higher bits
    buf = command & 0xF0 | 0x0C
    BUS.write_byte(LCD_ADDR, buf)
    time.sleep(TW)
    BUS.write_byte(LCD_ADDR, buf & 0xFB)
    # Write lower bits    
    buf = ((command & 0xF) << 4) | 0x0C
    BUS.write_byte(LCD_ADDR, buf)
    time.sleep(TW)
    BUS.write_byte(LCD_ADDR, buf & 0xFB)

# Write one byte command by dividing higher and lower 4bits

def write_command(command):

# Write higher bits

buf = command & 0xF0 | 0x0C

BUS.write_byte(LCD_ADDR, buf)

time.sleep(TW)

BUS.write_byte(LCD_ADDR, buf & 0xFB)

# Write lower bits

buf = ((command & 0xF) << 4) | 0x0C

BUS.write_byte(LCD_ADDR, buf)

time.sleep(TW)

BUS.write_byte(LCD_ADDR, buf & 0xFB)

実行部分の先頭で、8ビットモードを確定してから4ビットモードを設定。

いろいろなサンプルコードで0x33→0x32とバイト単位で書き込む例が多いが、4ビットごとの待機時間を意識するならこの方がデータシートの説明とも合っている。

# Set 8bit mode initially
write_4bits(0x3)
time.sleep(0.005)
write_4bits(0x3)
time.sleep(0.001)
write_4bits(0x3)
# Set 4bit mode
write_4bits(0x2)

# Set 8bit mode initially

write_4bits(0x3)

time.sleep(0.005)

write_4bits(0x3)

time.sleep(0.001)

write_4bits(0x3)

# Set 4bit mode

write_4bits(0x2)

最後にコマンド送信。

# Commands
# Function set: 001(DL)|NFxx
# DL=0(4bit mode)
# N=1(2 lines)
# F=0(5x8 font)
write_command(0x28)
time.sleep(0.002)
# Display ON/OFF: 0000|1DCB
# D=1(display ON)
# C=1(Cursor ON)
# B=1(Blink ON)
write_command(0x0F)
time.sleep(0.002)
# Clear Display: 0000|0001
write_command(0x01)
time.sleep(0.002)

# Commands

# Function set: 001(DL)|NFxx

# DL=0(4bit mode)

# N=1(2 lines)

# F=0(5x8 font)

write_command(0x28)

time.sleep(0.002)

# Display ON/OFF: 0000|1DCB

# D=1(display ON)

# C=1(Cursor ON)

# B=1(Blink ON)

write_command(0x0F)

time.sleep(0.002)

# Clear Display: 0000|0001

write_command(0x01)

time.sleep(0.002)

まず001で始まるFunction setで0b00101000＝0x28とする。

DL=0で4ビットモード
N=1で2行表示
F=0で5×8フォントを使用

次に00001で始まるDisplay ONで0b00001111＝0x0Fとする。

D=1でディスプレイ表示
C=1でカーソル表示
B=1でブリンクさせる

最後に0b00000001=0x01でディスプレイをクリア。

文字表示

先のコードに変更・追加を加えて、LCDに文字を表示してみる。

import smbus2 as smbus
import time

# Set constants
BUS = smbus.SMBus(1)
LCD_ADDR = 0x27
TW = 0.001 # pulse with for enable

# Write 4bits
def write_4bits(bits):
    buf = (bits & 0xF) << 4
    # 0xC: BL=1, E=1, R/W=0, RS=0
    BUS.write_byte(LCD_ADDR, buf | 0x0C)
    time.sleep(TW)
    # 0xFB: 1011 -> only E=0
    BUS.write_byte(LCD_ADDR, buf & 0xFB)

# Write one byte command by dividing higher and lower 4bits
def write_byte(command, is_command):
    lower_bits = 0x0C if is_command else 0x0D
    # Write higher bits
    buf = command & 0xF0 | lower_bits
    BUS.write_byte(LCD_ADDR, buf)
    time.sleep(TW)
    BUS.write_byte(LCD_ADDR, buf & 0xFB)
    # Write lower bits    
    buf = ((command & 0xF) << 4) | lower_bits
    BUS.write_byte(LCD_ADDR, buf)
    time.sleep(TW)
    BUS.write_byte(LCD_ADDR, buf & 0xFB)

# Write a character to specified addres
def write_char(char, addr=None):
    # Set address if specified
    if addr:
        write_byte(0x80 | (addr & 0xFF), is_command=True)
    # Write character to current addres
    write_byte(char, is_command=False)

# Set 8bit mode initially
write_4bits(0x3)
time.sleep(0.005)
write_4bits(0x3)
time.sleep(0.001)
write_4bits(0x3)
# Set 4bit mode
write_4bits(0x2)

# Commands
# Function set: 001(DL)|NFxx
# DL=0(4bit mode), N=1(2 lines), F=0(5x8 font)
write_byte(0x28, is_command=True)
# Display ON/OFF: 0000|1DCB
# D=1(display ON), C=0(Cursor OFF), B=0(Blink OFF)
write_byte(0x0C, is_command=True)
# Clear Display: 0000|0001
write_byte(0x01, is_command=True)

# Write characters
# First line - alphabet
write_char(0x41, 0x00)
write_char(0x42)
write_char(0x43)
# Second line - kana
write_char(0xB1, 0x40)
write_char(0xB2)
write_char(0xB3)

import smbus2 as smbus

import time

# Set constants

BUS = smbus.SMBus(1)

LCD_ADDR = 0x27

TW = 0.001 # pulse with for enable

# Write 4bits

def write_4bits(bits):

buf = (bits & 0xF) << 4

# 0xC: BL=1, E=1, R/W=0, RS=0

BUS.write_byte(LCD_ADDR, buf | 0x0C)

time.sleep(TW)

# 0xFB: 1011 -> only E=0

BUS.write_byte(LCD_ADDR, buf & 0xFB)

# Write one byte command by dividing higher and lower 4bits

def write_byte(command, is_command):

lower_bits = 0x0C if is_command else 0x0D

# Write higher bits

buf = command & 0xF0 | lower_bits

BUS.write_byte(LCD_ADDR, buf)

time.sleep(TW)

BUS.write_byte(LCD_ADDR, buf & 0xFB)

# Write lower bits

buf = ((command & 0xF) << 4) | lower_bits

BUS.write_byte(LCD_ADDR, buf)

time.sleep(TW)

BUS.write_byte(LCD_ADDR, buf & 0xFB)

# Write a character to specified addres

def write_char(char, addr=None):

# Set address if specified

if addr:

write_byte(0x80 | (addr & 0xFF), is_command=True)

# Write character to current addres

write_byte(char, is_command=False)

# Set 8bit mode initially

write_4bits(0x3)

time.sleep(0.005)

write_4bits(0x3)

time.sleep(0.001)

write_4bits(0x3)

# Set 4bit mode

write_4bits(0x2)

# Commands

# Function set: 001(DL)|NFxx

# DL=0(4bit mode), N=1(2 lines), F=0(5x8 font)

write_byte(0x28, is_command=True)

# Display ON/OFF: 0000|1DCB

# D=1(display ON), C=0(Cursor OFF), B=0(Blink OFF)

write_byte(0x0C, is_command=True)

# Clear Display: 0000|0001

write_byte(0x01, is_command=True)

# Write characters

# First line - alphabet

write_char(0x41, 0x00)

write_char(0x42)

write_char(0x43)

# Second line - kana

write_char(0xB1, 0x40)

write_char(0xB2)

write_char(0xB3)

まず、write_command関数をwrite_byte関数に変更し、引数is_commandのTrue/Falseに応じてRSの0/1を切替え、コマンド・データの両方を取り扱えるようにした。

データ送信の場合イネーブル時にRS=0となるため、下位4ビットはKE(RW)(RS)=0b1101=0xDとなる

# Write one byte command by dividing higher and lower 4bits
def write_byte(command, is_command):
    lower_bits = 0x0C if is_command else 0x0D
    # Write higher bits
    buf = command & 0xF0 | lower_bits
    BUS.write_byte(LCD_ADDR, buf)
    time.sleep(TW)
    BUS.write_byte(LCD_ADDR, buf & 0xFB)
    # Write lower bits    
    buf = ((command & 0xF) << 4) | lower_bits
    BUS.write_byte(LCD_ADDR, buf)
    time.sleep(TW)
    BUS.write_byte(LCD_ADDR, buf & 0xFB)

# Write one byte command by dividing higher and lower 4bits

def write_byte(command, is_command):

lower_bits = 0x0C if is_command else 0x0D

# Write higher bits

buf = command & 0xF0 | lower_bits

BUS.write_byte(LCD_ADDR, buf)

time.sleep(TW)

BUS.write_byte(LCD_ADDR, buf & 0xFB)

# Write lower bits

buf = ((command & 0xF) << 4) | lower_bits

BUS.write_byte(LCD_ADDR, buf)

time.sleep(TW)

BUS.write_byte(LCD_ADDR, buf & 0xFB)

また、新たに文字を表示する関数write_charを定義した。アドレスが与えられた場合はDDRAMのそのアドレスに、アドレスを指定しない場合は現在のアドレスに文字を書き込む。1文字書き込むとアドレスはインクリメントされるため、続けて文字を書き込む場合にはアドレス指定はしなくてよい。

# Write a character to specified addres
def write_char(char, addr=None):
    # Set address if specified
    if addr:
        write_byte(0x80 | (addr & 0xFF), is_command=True)
    # Write character to current addres
    write_byte(char, is_command=False)

# Write a character to specified addres

def write_char(char, addr=None):

# Set address if specified

if addr:

write_byte(0x80 | (addr & 0xFF), is_command=True)

# Write character to current addres

write_byte(char, is_command=False)

実行の前半では、カーソルOFF、ブリンクOFFとしている。

# Display ON/OFF: 0000|1DCB
# D=1(display ON), C=0(Cursor OFF), B=0(Blink OFF)
write_byte(0x0C, is_command=True)

# Display ON/OFF: 0000|1DCB

# D=1(display ON), C=0(Cursor OFF), B=0(Blink OFF)

write_byte(0x0C, is_command=True)

文字表示の部分は以下の通りで、1行目に”ABC”、2行目に半角カナで”ｱｲｳ”と表示している。

# Write characters
# First line - alphabet
write_char(0x41, 0x00)
write_char(0x42)
write_char(0x43)
# Second line - kana
write_char(0xB1, 0x40)
write_char(0xB2)
write_char(0xB3)

# Write characters

# First line - alphabet

write_char(0x41, 0x00)

write_char(0x42)

write_char(0x43)

# Second line - kana

write_char(0xB1, 0x40)

write_char(0xB2)

write_char(0xB3)

LCD1602クラス

LCD1602を扱うクラスを作成。これまで作った関数をクラスのメソッドにしただけ。インスタンス生成時にLCDのアドレスを与える。

import smbus2 as smbus
import time

# Class to manipuoate LCD1602
class LCD1602:
    # Set constants
    BUS = smbus.SMBus(1)
    TW = 0.001 # pulse with for enable

    # Create an instance by specifying LCD Address
    def __init__(self, lcd_addr):
        self.lcd_addr = lcd_addr
        # Set 8bit mode initially
        self._write_4bits(0x3)
        time.sleep(0.005)
        self._write_4bits(0x3)
        time.sleep(0.001)
        self._write_4bits(0x3)
        # Set 4bit mode
        self._write_4bits(0x2)

        # Commands
        # Function set: 001(DL)|NFxx
        # DL=0(4bit mode), N=1(2 lines), F=0(5x8 font)
        self._write_byte(0x28, is_command=True)
        # Display ON/OFF: 0000|1DCB
        # D=1(display ON), C=0(Cursor OFF), B=0(Blink OFF)
        self._write_byte(0x0C, is_command=True)
        # Clear Display: 0000|0001
        self._write_byte(0x01, is_command=True)

    # Write 4bits
    def _write_4bits(self, bits):
        buf = (bits & 0xF) << 4
        # 0xC: BL=1, E=1, R/W=0, RS=0
        self.BUS.write_byte(self.lcd_addr, buf | 0x0C)
        time.sleep(self.TW)
        # 0xFB: 1011 -> only E=0
        self.BUS.write_byte(self.lcd_addr, buf & 0xFB)


    # Write one byte command by dividing higher and lower 4bits
    def _write_byte(self, command, is_command):
        lower_bits = 0x0C if is_command else 0x0D
        # Write higher bits
        buf = command & 0xF0 | lower_bits
        self.BUS.write_byte(self.lcd_addr, buf)
        time.sleep(self.TW)
        self.BUS.write_byte(self.lcd_addr, buf & 0xFB)
        # Write lower bits    
        buf = ((command & 0xF) << 4) | lower_bits
        self.BUS.write_byte(self.lcd_addr, buf)
        time.sleep(self.TW)
        self.BUS.write_byte(self.lcd_addr, buf & 0xFB)

    # Write a character to specified addres
    def write_char(self, char_cord, addr=None):
        # Set address if specified
        if addr:
            self._write_byte(0x80 | (addr & 0xFF), is_command=True)
        # Write character to current addres
        self._write_byte(char_cord, is_command=False)
    
    # Write string specifying line and start position
    def write_string(self, str, line=1, start_pos=1):
        addr = 0x00 if line==1 else 0x40
        addr += start_pos
        for char in str:
            self.write_char(ord(char), addr)
            addr += 1

# Create instance of LCD
lcd = LCD1602(0x27)
# Write string to the first line
lcd.write_string('Welcome', line=1, start_pos=4)
# Write characters to the second line ('Youkoso' in Kana)
lcd.write_char(0xD6, 0x45)
lcd.write_char(0xB3)
lcd.write_char(0xBA)
lcd.write_char(0xBF)

import smbus2 as smbus

import time

# Class to manipuoate LCD1602

class LCD1602:

# Set constants

BUS = smbus.SMBus(1)

TW = 0.001 # pulse with for enable

# Create an instance by specifying LCD Address

def __init__(self, lcd_addr):

self.lcd_addr = lcd_addr

# Set 8bit mode initially

self._write_4bits(0x3)

time.sleep(0.005)

self._write_4bits(0x3)

time.sleep(0.001)

self._write_4bits(0x3)

# Set 4bit mode

self._write_4bits(0x2)

# Commands

# Function set: 001(DL)|NFxx

# DL=0(4bit mode), N=1(2 lines), F=0(5x8 font)

self._write_byte(0x28, is_command=True)

# Display ON/OFF: 0000|1DCB

# D=1(display ON), C=0(Cursor OFF), B=0(Blink OFF)

self._write_byte(0x0C, is_command=True)

# Clear Display: 0000|0001

self._write_byte(0x01, is_command=True)

# Write 4bits

def _write_4bits(self, bits):

buf = (bits & 0xF) << 4

# 0xC: BL=1, E=1, R/W=0, RS=0

self.BUS.write_byte(self.lcd_addr, buf | 0x0C)

time.sleep(self.TW)

# 0xFB: 1011 -> only E=0

self.BUS.write_byte(self.lcd_addr, buf & 0xFB)

# Write one byte command by dividing higher and lower 4bits

def _write_byte(self, command, is_command):

lower_bits = 0x0C if is_command else 0x0D

# Write higher bits

buf = command & 0xF0 | lower_bits

self.BUS.write_byte(self.lcd_addr, buf)

time.sleep(self.TW)

self.BUS.write_byte(self.lcd_addr, buf & 0xFB)

# Write lower bits

buf = ((command & 0xF) << 4) | lower_bits

self.BUS.write_byte(self.lcd_addr, buf)

time.sleep(self.TW)

self.BUS.write_byte(self.lcd_addr, buf & 0xFB)

# Write a character to specified addres

def write_char(self, char_cord, addr=None):

# Set address if specified

if addr:

self._write_byte(0x80 | (addr & 0xFF), is_command=True)

# Write character to current addres

self._write_byte(char_cord, is_command=False)

# Write string specifying line and start position

def write_string(self, str, line=1, start_pos=1):

addr = 0x00 if line==1 else 0x40

addr += start_pos

for char in str:

self.write_char(ord(char), addr)

addr += 1

# Create instance of LCD

lcd = LCD1602(0x27)

# Write string to the first line

lcd.write_string('Welcome', line=1, start_pos=4)

# Write characters to the second line ('Youkoso' in Kana)

lcd.write_char(0xD6, 0x45)

lcd.write_char(0xB3)

lcd.write_char(0xBA)

lcd.write_char(0xBF)

I2C

2023-02-11 / tau / コメントする

概要

I2C（I squared C）はフィリップス社で開発されたシリアルバス。正式な呼称はInter-Integrated Circuitの略で表記はI²Cと上付きが本来とのこと。

マスターに対して1つ以上のスレーブを繋ぐことができて、接続はクロック線（SCL）とデータ線（SDA）の2本だけで済む。マスターからスレーブを指定して、Read/Write信号によりデータを書き込んだり読み込んだりすることができる。

原理（マスターからスレーブへの書き込み）

ビットデータの転送

データはクロック信号に同期してビット情報を転送。SCLの立ち上がり開始から立ち下がり開始までの間にデータを転送する。データを変更（H ⇔ L）する場合には、SCLがLの間にSDAを変更する。

スタートコンディション／ストップコンディション

データ転送のためSCLがHの間にSDAは変化させないが、この間にSDAが変化した場合は不正・無効ではなく、スタートコンディション／ストップコンディションの意味を持つ。

SDAがH→Lに変化した場合はスタートコンディションで、SCLがH→LになったあとLの間に最初のビットの準備をする。

SDAがL→Hに変化した場合はストップコンディションで、その前にSCLがLの間にSDAをLにしてストップコンディションの準備をする。

バイトデータの転送

データはバイト単位で転送される。

マスターからスレーブへの書き込みの場合、フォーマットは以下の様になる（スレーブアドレスが7ビットの場合）。

マスターからスタートコンディション、スレーブアドレス7ビット、RW = 0を送信
指定されたアドレスのスレーブからACK送信→マスターで受信
マスターから1バイトのデータを送信
スレーブがデータ受信後、ACK送信→マスターで受信
以降、必要バイト数を送信
送信終了後、マスターからストップコンディション送信

マスターがスレーブのデータを読み込む場合には、フォーマットは以下の様になる。

マスターからスタートコンディション、スレーブアドレス7ビット、RW = 1を送信
指定されたアドレスのスレーブからACK送信→マスターで受信
スレーブから1バイトのデータを送信
マスターが受信後、ACK送信→スレーブで受信
以降、必要バイト数を受信
受信終了後、マスターからストップコンディション送信

スレーブアドレス送信とRW

マスターからスレーブに対してスタートコンディションを送信し、各スレーブが受信体勢に入る。その後マスターからスレーブアドレスを送信する。

スレーブアドレスが7ビットの場合、MSBから順に7ビット送り、最後にRWを1ビットで送る。RW=1のときマスター側が読み取り、RW=0のときマスターからスレーブへ書き込み。

ACK

I2Cのデータは8ビット単位で転送され、その後にACK/NACKが返される。マスターからスレーブへの書き込みの場合ACKはスレーブからバスに発信され、マスターがスレーブから読み出す場合はマスターから発信される。

スレーブアドレス指定の際、選択されたスレーブはACK信号を1ビットのLで返す。選択されなかったスレーブはストップコンディションを待機。何らかの理由でスレーブ側がデータを受け取れなかったときはNAK信号を1ビットのHで返す。

マスターからスレーブへデータを書き込む場合、8ビット目の送信後にSCLをLにし、スレーブからACKを受け取ってから次のデータの送信を開始する。

マスターがスレーブからデータを読み込む場合、アドレスは上記と同じだが、データについてはマスターがデータ受信後にACKを送る。

ただしスレーブ側で次のクロックサイクルに合わせてデータを送るのに間に合わない場合、スレーブ側でSCLを強制的にLにして、マスターでのデータ読み込みを抑制する（クロックストレッチ）。スレーブの準備完了後にクロックストレッチは解除され、データの読み込みが再開される。

I2Cの有効化

Raspberry PiでI2Cを有効化する手順。

コマンドラインでsudo raspi-configを実行
画面が変わるので、5 Interfacing Optionsを選択
P5 I2Cを選択

I2Cツール

LinuxベースのRaspberry Piで利用可能なツール。

i2cdetect

sudo i2cdetect ...で実行。Raspberry Piで管理者権限を持っているなら、sudoなしでもok。

i2cdetect -V

バージョン確認。

$ i2cdetect -V
i2cdetect version 4.1

1 2	$ i2cdetect -V i2cdetect version 4.1

i2cdetect -l

利用可能なバスの一覧を表示。

$ i2cdetect -l
i2c-1	i2c       	bcm2835 (i2c@7e804000)          	I2C adapter

1 2	$ i2cdetect -l i2c-1 i2c bcm2835 (i2c@7e804000) I2C adapter

i2c-1の'1'がバス番号になる。

i2cdetect -F [bus]

指定したバスで利用可能な機能の一覧を表示。

$ i2cdetect -F 1
Functionalities implemented by /dev/i2c-1:
I2C                              yes
SMBus Quick Command              yes
SMBus Send Byte                  yes
SMBus Receive Byte               yes
SMBus Write Byte                 yes
SMBus Read Byte                  yes
SMBus Write Word                 yes
SMBus Read Word                  yes
SMBus Process Call               yes
SMBus Block Write                yes
SMBus Block Read                 no
SMBus Block Process Call         no
SMBus PEC                        yes
I2C Block Write                  yes
I2C Block Read                   yes

$ i2cdetect -F 1

Functionalities implemented by /dev/i2c-1:

I2C yes

SMBus Quick Command yes

SMBus Send Byte yes

SMBus Receive Byte yes

SMBus Write Byte yes

SMBus Read Byte yes

SMBus Write Word yes

SMBus Read Word yes

SMBus Process Call yes

SMBus Block Write yes

SMBus Block Read no

SMBus Block Process Call no

SMBus PEC yes

I2C Block Write yes

I2C Block Read yes

i2cdetect -y [bus]

指定したバスのデバイスアドレスを表示する。

$ i2cdetect -y 1
     0  1  2  3  4  5  6  7  8  9  a  b  c  d  e  f
00:          -- -- -- -- -- -- -- -- -- -- -- -- -- 
10: -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- 
20: -- -- -- -- -- -- -- 27 -- -- -- -- -- -- -- -- 
30: -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- 
40: -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- 
50: -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- 
60: -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- 
70: -- -- -- -- -- -- -- --

$ i2cdetect -y 1

0 1 2 3 4 5 6 7 8 9 a b c d e f

00: -- -- -- -- -- -- -- -- -- -- -- -- --

10: -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- --

20: -- -- -- -- -- -- -- 27 -- -- -- -- -- -- -- --

30: -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- --

40: -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- --

50: -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- --

60: -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- --

70: -- -- -- -- -- -- -- --

各行の2桁目がアドレスの上位桁、各列がアドレスの下位桁を表していて、ここではデバイスアドレスが1つ（0x27）確認できる。

ライブラリー

Raspberry PiとPythonでI2Cを扱うためのライブラリーsmbus2について（ドキュメントはこちら）。

sudo pip install smbus2でインストール。SMBusはSystem Management Busの略でI2Cのプロトコルと概ね同じ。

smbus2モジュールのSMBusクラスでバスへアクセスするインスタンスを取得。コンストラクターの引数にはバス番号を指定。バス番号はsudo i2cdetectで確認されたバス番号。

import smbus2 as smbus

bus = smbus.SMBus(1)

import smbus2 as smbus

bus = smbus.SMBus(1)

以降、read_byteやwrite_byteなど、このインスタンスのメソッドを使う。

Raspberry Pi – シフトレジスター～ドットマトリックスLED

2023-01-30 / tau / コメントする

概要

Raspberry Piで8×8のドットマトリックスLEDを表示させてみた。

2つのシフトレジスターを使って、任意のパターンを表示させるようにした
パターンを周期的に流れるように表示させた

ドットマトリックスLEDの仕様

キットに同梱されていたドットマトリックスLEDはピン配置や極性の手掛かりになる表示などがなかったので、1つずつ通電しながらピン配置と点灯の確認を行った。

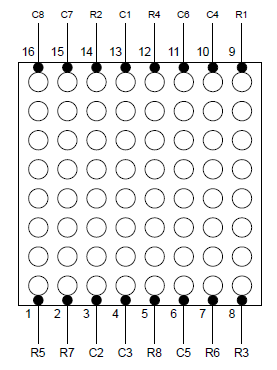
内部の接続は以下のようになっている。RmをHIGHに、CnをLOWにすると、m行目n列目のLEDが点灯する。

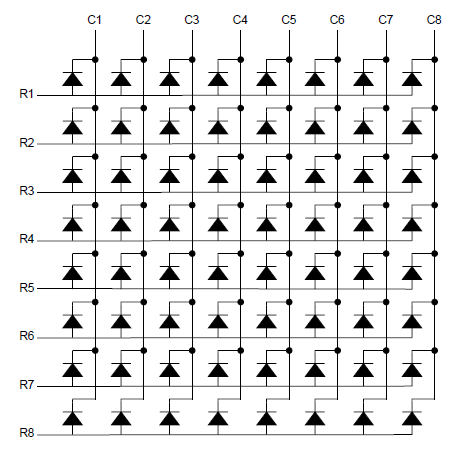
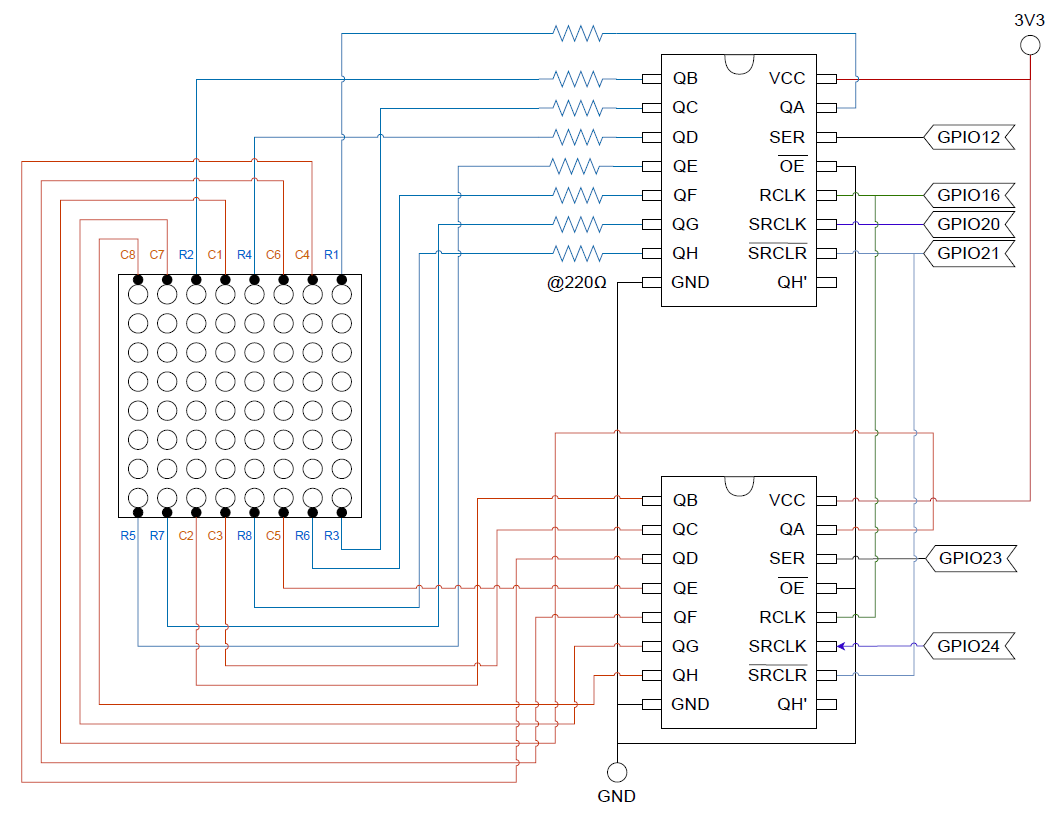
回路図

キットのマニュアルの回路は2つのシフトレジスター74HC595を使っていたが、それらをカスケードに接続しているため、行と列のパターンを同時にしか設定できない。

そこで、2つのシフトレジスターを切り離して独立して制御するようにした。1行ずつスキャンしながら行ごとの点灯パターンを設定し、8×8の64個のLEDを任意のパターンで点灯させることができる。

ブレッドボードで回路を組んだら、かなり配線がごちゃごちゃになった。LEDのRとCから8本ずつのケーブルが出て、保護抵抗も8本使っているので仕方がないか。LEDのサイズがそれなりに大きいので、ブレッドボードの穴が覆われてしまう。

表示は平仮名の「お」で、後述のサイネージコードで「おはよう」と流して表示しているときの一部。

コード例

試験点灯

まず、8×8のドットパターンを2秒間だけ表示させてみる。

import RPi.GPIO as GPIO
import time
import threading
import lib.led_dotmatrix_data as data

# Set GPIO pin number in BCM
SER_R = 12
SER_C = 23
SRCLK_R = 20
SRCLK_C = 24
RCLK = 16
SRCLR = 21
ROWS = [0x80, 0x40, 0x20, 0x10, 0x08, 0x04, 0x02, 0x01]

# Initialize all pins
def initialize():
    GPIO.setmode(GPIO.BCM)
    GPIO.setup(SER_R, GPIO.OUT, initial=GPIO.LOW)
    GPIO.setup(SER_C, GPIO.OUT, initial=GPIO.LOW)
    GPIO.setup(SRCLK_R, GPIO.OUT, initial=GPIO.LOW)
    GPIO.setup(SRCLK_C, GPIO.OUT, initial=GPIO.LOW)
    GPIO.setup(RCLK, GPIO.OUT, initial=GPIO.LOW)
    GPIO.setup(SRCLR, GPIO.OUT, initial=GPIO.HIGH)

# Input a bit to shift register
def shift(ser, serclk, level):
    GPIO.output(ser, level)
    GPIO.output(serclk, GPIO.HIGH)
    GPIO.output(serclk, GPIO.LOW)

# Read value in the storage register
def read():
    GPIO.output(RCLK, GPIO.HIGH)
    GPIO.output(RCLK, GPIO.LOW)

# Clear all the LEDs of dotmatrix LED
def clear():
    for i in range(8):
        shift(SER_R, SRCLK_R, GPIO.LOW)
        shift(SER_C, SRCLK_C, GPIO.LOW)
    read()

# Display pattern to dotmatrix LED during sleeptime
def display(pattern, sleeptime):
    for row, colpattern in zip(ROWS, pattern):
        for i in range(8):
            shift(SER_R, SRCLK_R, (row >> i) & 1)
        for i in range(8):
            shift(SER_C, SRCLK_C, not((colpattern >> i) & 1))
        read()
        time.sleep(sleeptime)

# Ending execution
def destroy():
    clear()
    GPIO.cleanup()

# Class inherited from Thread to display dotmatrix LED
class DisplayThread(threading.Thread):
    def __init__(self,bit_pattern):
        threading.Thread.__init__(self)
        self.is_running = True
        self.bit_pattern = bit_pattern
    
    def run(self):
        while self.is_running:
            display(self.bit_pattern, 0.001)
    
    def stop(self):
        self.is_running = False

# Main process

initialize()
clear()

t = DisplayThread(data.get_bit_pattern(data.SMILE))
t.start()
time.sleep(2.0)
t.stop()
time.sleep(0.01) # <- Without this line, runtime error occurs requiring setmode
destroy()

import RPi.GPIO as GPIO

import time

import threading

import lib.led_dotmatrix_data as data

# Set GPIO pin number in BCM

SER_R = 12

SER_C = 23

SRCLK_R = 20

SRCLK_C = 24

RCLK = 16

SRCLR = 21

ROWS = [0x80, 0x40, 0x20, 0x10, 0x08, 0x04, 0x02, 0x01]

# Initialize all pins

def initialize():

GPIO.setmode(GPIO.BCM)

GPIO.setup(SER_R, GPIO.OUT, initial=GPIO.LOW)

GPIO.setup(SER_C, GPIO.OUT, initial=GPIO.LOW)

GPIO.setup(SRCLK_R, GPIO.OUT, initial=GPIO.LOW)

GPIO.setup(SRCLK_C, GPIO.OUT, initial=GPIO.LOW)

GPIO.setup(RCLK, GPIO.OUT, initial=GPIO.LOW)

GPIO.setup(SRCLR, GPIO.OUT, initial=GPIO.HIGH)

# Input a bit to shift register

def shift(ser, serclk, level):

GPIO.output(ser, level)

GPIO.output(serclk, GPIO.HIGH)

GPIO.output(serclk, GPIO.LOW)

# Read value in the storage register

def read():

GPIO.output(RCLK, GPIO.HIGH)

GPIO.output(RCLK, GPIO.LOW)

# Clear all the LEDs of dotmatrix LED

def clear():

for i in range(8):

shift(SER_R, SRCLK_R, GPIO.LOW)

shift(SER_C, SRCLK_C, GPIO.LOW)

read()

# Display pattern to dotmatrix LED during sleeptime

def display(pattern, sleeptime):

for row, colpattern in zip(ROWS, pattern):

for i in range(8):

shift(SER_R, SRCLK_R, (row >> i) & 1)

for i in range(8):

shift(SER_C, SRCLK_C, not((colpattern >> i) & 1))

read()

time.sleep(sleeptime)

# Ending execution

def destroy():

clear()

GPIO.cleanup()

# Class inherited from Thread to display dotmatrix LED

class DisplayThread(threading.Thread):

def __init__(self,bit_pattern):

threading.Thread.__init__(self)

self.is_running = True

self.bit_pattern = bit_pattern

def run(self):

while self.is_running:

display(self.bit_pattern, 0.001)

def stop(self):

self.is_running = False

# Main process

initialize()

clear()

t = DisplayThread(data.get_bit_pattern(data.SMILE))

t.start()

time.sleep(2.0)

t.stop()

time.sleep(0.01) # <- Without this line, runtime error occurs requiring setmode

destroy()

ドットパターンはサブディレクトリーlibの下にled_dotmatrix_data.pyとして以下のモジュールを準備した。

# This module is imported by led_dotmatrix control programs.

# Function to convert 8x8 string pattern to bit pattern
def get_bit_pattern(string_array):
    pattern = []
    for str in string_array:
        bin = 0
        for n in range(8):
            digit = 0 if str[n] == ' ' else 1
            bin = bin | (digit << (7 - n))
        pattern.append(bin)
    return pattern

SMILE = [
    '  ****  ',
    ' *    * ',
    '* *  * *',
    '*      *',
    '* *  * *',
    '*  **  *',
    ' *    * ',
    '  ****  ',
]

# This module is imported by led_dotmatrix control programs.

# Function to convert 8x8 string pattern to bit pattern

def get_bit_pattern(string_array):

pattern = []

for str in string_array:

bin = 0

for n in range(8):

digit = 0 if str[n] == ' ' else 1

bin = bin | (digit << (7 - n))

pattern.append(bin)

return pattern

SMILE = [

' **** ',

' * * ',

'* * * *',

'* *',

'* * * *',

'* ** *',

' * * ',

' **** ',

]

パターンをスペースとスペース以外の文字（ここでは*）を使って準備し、get_bit_pattern関数で8ビット×8行のリストとする。

最初のコードで、まずGPIOピンなどの定数を定義している。ROWSはドットマトリックスの各行を単独で指定する際に、シフトレジスターに与えるビットパターン。

# Set GPIO pin number in BCM
SER_R = 12
SER_C = 23
SRCLK_R = 20
SRCLK_C = 24
RCLK = 16
SRCLR = 21
ROWS = [0x80, 0x40, 0x20, 0x10, 0x08, 0x04, 0x02, 0x01]

# Set GPIO pin number in BCM

SER_R = 12

SER_C = 23

SRCLK_R = 20

SRCLK_C = 24

RCLK = 16

SRCLR = 21

ROWS = [0x80, 0x40, 0x20, 0x10, 0x08, 0x04, 0x02, 0x01]

shift関数は、SERとSRCLK、HIGH/LOWのレベルを指定してシフトレジスターを1回シフトする。

# Input a bit to shift register
def shift(ser, serclk, level):
    GPIO.output(ser, level)
    GPIO.output(serclk, GPIO.HIGH)
    GPIO.output(serclk, GPIO.LOW)

# Input a bit to shift register

def shift(ser, serclk, level):

GPIO.output(ser, level)

GPIO.output(serclk, GPIO.HIGH)

GPIO.output(serclk, GPIO.LOW)

read関数は、RCLKをHIGHにしてストレージレジスタ―の出力を取り出し、LOWに戻す。

# Read value in the storage register
def read():
    GPIO.output(RCLK, GPIO.HIGH)
    GPIO.output(RCLK, GPIO.LOW)

# Read value in the storage register

def read():

GPIO.output(RCLK, GPIO.HIGH)

GPIO.output(RCLK, GPIO.LOW)

clear関数はドットマトリックスのR1～R8をLOWにしてLEDを消灯させる。念のためC1～C8もLOWにしている。

# Clear all the LEDs of dotmatrix LED
def clear():
    for i in range(8):
        shift(SER_R, SRCLK_R, GPIO.LOW)
        shift(SER_C, SRCLK_C, GPIO.LOW)
    read()

# Clear all the LEDs of dotmatrix LED

def clear():

for i in range(8):

shift(SER_R, SRCLK_R, GPIO.LOW)

shift(SER_C, SRCLK_C, GPIO.LOW)

read()

display関数は、8ビット×8行のビットパターンを与えてsleepの秒数だけLEDを点灯させる。

# Display pattern to dotmatrix LED during sleeptime
def display(pattern, sleeptime):
    for row, colpattern in zip(ROWS, pattern):
        for i in range(8):
            shift(SER_R, SRCLK_R, (row >> i) & 1)
        for i in range(8):
            shift(SER_C, SRCLK_C, not((colpattern >> i) & 1))
        read()
        time.sleep(sleeptime)

# Display pattern to dotmatrix LED during sleeptime

def display(pattern, sleeptime):

for row, colpattern in zip(ROWS, pattern):

for i in range(8):

shift(SER_R, SRCLK_R, (row >> i) & 1)

for i in range(8):

shift(SER_C, SRCLK_C, not((colpattern >> i) & 1))

read()

time.sleep(sleeptime)

DisplayThreadはビットパターンを与えて生成し、startメソッドを呼ぶと内部でrunメソッドが実行される。stopメソッドによりスレッドが停止する。

# Class inherited from Thread to display dotmatrix LED
class DisplayThread(threading.Thread):
    def __init__(self, bit_pattern):
        threading.Thread.__init__(self)
        self.is_running = True
        self.bit_pattern = bit_pattern
    
    def run(self):
        while self.is_running:
            display(self.bit_pattern, 0.001)
    
    def stop(self):
        self.is_running = False

# Class inherited from Thread to display dotmatrix LED

class DisplayThread(threading.Thread):

def __init__(self, bit_pattern):

threading.Thread.__init__(self)

self.is_running = True

self.bit_pattern = bit_pattern

def run(self):

while self.is_running:

display(self.bit_pattern, 0.001)

def stop(self):

self.is_running = False

試験点灯用のコードは以下の通りで、表示パターンを与えてスレッドを生成し、2秒間点灯させた後にスレッドを停止させている。

ここで、stopメソッドの後に僅かな時間の間をおかないと、「setmodeが必要」というランタイムエラーが出る。destroyメソッドでcleanupを実行するタイミングがstopで表示が停止するよりも早いからかもしれない。

initialize()
clear()

t = DisplayThread(data.get_bit_pattern(data.SMILE))
t.start()
time.sleep(2.0)
t.stop()
time.sleep(0.01) # <- Without this line, runtime error occurs requiring setmode
destroy()

initialize()

clear()

t = DisplayThread(data.get_bit_pattern(data.SMILE))

t.start()

time.sleep(2.0)

t.stop()

time.sleep(0.01) # <- Without this line, runtime error occurs requiring setmode

destroy()

CTRL-Cでの表示停止

次に、実行後表示を続けてCTRL-Cのキーボード入力で停止するようにした。

このとき、キーボード割込を待ち受けるwhileループの内容を単にpassとすると目に見えるくらいのちらつきが生じたため、sleepを入れている。

try:
    t = DisplayThread(data.get_bit_pattern(data.SMILE))
    t.start()
    while True:
        time.sleep(1) # <- Flicks when this line is 'pass' rather than this
except KeyboardInterrupt:
    print('STOP')
    t.stop()
    time.sleep(0.1)
    destroy()

try:

t = DisplayThread(data.get_bit_pattern(data.SMILE))

t.start()

while True:

time.sleep(1) # <- Flicks when this line is 'pass' rather than this

except KeyboardInterrupt:

print('STOP')

t.stop()

time.sleep(0.1)

destroy()

アニメーション表示

2つのパターンを準備して、一定時間で交互に表示を切り替えてみた。

まず、led_dotmatrix_dataモジュールで準備した表示パターンは以下の通り。

# Define two patterns lists to be displayed alternately
SMILE = [
    '  ****  ',
    ' *    * ',
    '* *  * *',
    '*      *',
    '* *  * *',
    '*  **  *',
    ' *    * ',
    '  ****  ',
]

WINK = [
    '  ****  ',
    ' *    * ',
    '* *    *',
    '*      *',
    '* *  * *',
    '*  **  *',
    ' *    * ',
    '  ****  ',
]

# Define two patterns lists to be displayed alternately

SMILE = [

' **** ',

' * * ',

'* * * *',

'* *',

'* * * *',

'* ** *',

' * * ',

' **** ',

]

WINK = [

' **** ',

' * * ',

'* * *',

'* *',

'* * * *',

'* ** *',

' * * ',

' **** ',

]

2つのパターンを交互に切り替える実行部分は以下の通り。

try:
    # Continue to display SMILE pattern and WINK pattern alternately
    while True:
        t = DisplayThread(data.get_bit_pattern(data.SMILE))
        t.start()
        time.sleep(1.0)
        t.stop()
        t = DisplayThread(data.get_bit_pattern(data.WINK))
        t.start()
        time.sleep(1.0)
        t.stop()
except KeyboardInterrupt:
    # Before cleanup, it's needed to (1)stop the thread, (2)wait a bit.
    # Otherwise, runtime error occurs requiring setmode.
    t.stop()
    time.sleep(0.1)
    destroy()

try:

# Continue to display SMILE pattern and WINK pattern alternately

while True:

t = DisplayThread(data.get_bit_pattern(data.SMILE))

t.start()

time.sleep(1.0)

t.stop()

t = DisplayThread(data.get_bit_pattern(data.WINK))

t.start()

time.sleep(1.0)

t.stop()

except KeyboardInterrupt:

# Before cleanup, it's needed to (1)stop the thread, (2)wait a bit.

# Otherwise, runtime error occurs requiring setmode.

t.stop()

time.sleep(0.1)

destroy()

流れる表示

8×8のパターンを横に流れるように表示してみた。led_dotmatrix_dataモジュールに以下を追加。

get_cycle_pattern関数は、8×8のパターンの表示開始位置を与えてサイクリックに表示をずらすためのパターンを返す関数。

# Retrieve 8x8 pattern from source list cyclically.
# Length of source list can be 8 or more
def get_cycle_pattern(org_pattern, start_col):
    pattern = []
    for i in range(8):
        n = start_col
        bin = 0
        for j in range(8):
            digit = 0 if org_pattern[i][n] == ' ' else 1
            bin = bin | (digit << (7 - j))
            n = n + 1 if n + 1 < len(org_pattern[i]) else 0
        pattern.append(bin)
    return pattern

# Dfine 8x8 pattern to be displayed in horizontal flow.
FLOW = [
    '  **        ',
    ' *  *       ',
    '*    *      ',
    '*    *      ',
    '      *    *',
    '      *    *',
    '       *  * ',
    '        **  ',
]

# Retrieve 8x8 pattern from source list cyclically.

# Length of source list can be 8 or more

def get_cycle_pattern(org_pattern, start_col):

pattern = []

for i in range(8):

n = start_col

bin = 0

for j in range(8):

digit = 0 if org_pattern[i][n] == ' ' else 1

bin = bin | (digit << (7 - j))

n = n + 1 if n + 1 < len(org_pattern[i]) else 0

pattern.append(bin)

return pattern

# Dfine 8x8 pattern to be displayed in horizontal flow.

FLOW = [

' ** ',

' * * ',

'* * ',

' * *',

' * * ',

' ** ',

]

以下は、この関数を使って流れる表示をさせるコード。データのリストの最後まで来たら、表示させる桁数を先頭に戻している。この結果、正弦波のような波が流れて表示される。

try:
    # Continue to display SMILE pattern and WINK pattern alternately
    col = 0
    while True:
        t = DisplayThread(data.get_cycle_pattern(data.FLOW, col))
        t.start()
        time.sleep(0.05)
        t.stop()
        col = col + 1 if col + 1 < len(data.FLOW[0]) else 0
except KeyboardInterrupt:
    # Before cleanup, it's needed to (1)stop the thread, (2)wait a bit.
    # Otherwise, runtime error occurs requiring setmode.
    t.stop()
    time.sleep(0.1)
    destroy()

try:

# Continue to display SMILE pattern and WINK pattern alternately

col = 0

while True:

t = DisplayThread(data.get_cycle_pattern(data.FLOW, col))

t.start()

time.sleep(0.05)

t.stop()

col = col + 1 if col + 1 < len(data.FLOW[0]) else 0

except KeyboardInterrupt:

# Before cleanup, it's needed to (1)stop the thread, (2)wait a bit.

# Otherwise, runtime error occurs requiring setmode.

t.stop()

time.sleep(0.1)

destroy()

サイネージ

複数の文字が横に流れるように表示させるようにしてみた。まず、led_dotmatrix_dataモジュールに以下の関数とパターンを追加。

combine_patterns関数は複数のパターンを引数にとり、それらを横に連ねた2次元リストを返す。

# Combine more than one patterns into a 2D list with 8 rows.
def combine_patterns(*patterns):
    result_pattern = [''] * 8

    for p in patterns:
        for r in range(8):
            result_pattern[r] += p[r]

    return result_pattern

# Define patterns for sinage 'OHAYO' in KANA
pko = [
    '  *     ',
    ' ***    ',
    '  * **  ',
    '  *   * ',
    ' *****  ',
    '*  *  * ',
    '*  *  * ',
    ' **  *  ',
]

pkha = [
    ' *  *   ',
    '* ***** ',
    '*   *   ',
    '*   *   ',
    '*   *   ',
    '*  ***  ',
    '*** * * ',
    '*  *  * ',
]

pkyo = [
    '   *    ',
    '   **** ',
    '   *    ',
    '   *    ',
    '   *    ',
    ' ****   ',
    '*  * *  ',
    ' **   * ',
]

pku =[
    '  ***   ',
    '        ',
    ' *****  ',
    '*     * ',
    '      * ',
    '      * ',
    '     *  ',
    '   *    ',
]

# Combine more than one patterns into a 2D list with 8 rows.

def combine_patterns(*patterns):

result_pattern = [''] * 8

for p in patterns:

for r in range(8):

result_pattern[r] += p[r]

return result_pattern

# Define patterns for sinage 'OHAYO' in KANA

pko = [

' * ',

' *** ',

' * ** ',

' * * ',

' ***** ',

'* * * ',

' ** * ',

]

pkha = [

' * * ',

'* ***** ',

'* * ',

'* *** ',

'*** * * ',

'* * * ',

]

pkyo = [

' * ',

' **** ',

' * ',

' **** ',

'* * * ',

' ** * ',

]

pku =[

' *** ',

' ',

' ***** ',

'* * ',

' * ',

]

実行部分は以下の通りで、複数の文字パターンを関数で1つの2次元リストにまとめ、それを上の流れる表示と同じように処理している。

#message = data.combine_patterns(data.ph, data.pe, data.pl, data.pl, data.po)
message = data.combine_patterns(data.pko, data.pkha, data.pkyo, data.pku)

initialize()
clear()

try:
    # Continue to display SMILE pattern and WINK pattern alternately
    col = 0
    while True:
        t = DisplayThread(data.get_cycle_pattern(message, col))
        t.start()
        time.sleep(0.1)
        t.stop()
        col = col + 1 if col + 1 < len(message[0]) else 0
except KeyboardInterrupt:
    # Before cleanup, it's needed to (1)stop the thread, (2)wait a bit.
    # Otherwise, runtime error occurs requiring setmode.
    t.stop()
    time.sleep(0.1)
    destroy()

#message = data.combine_patterns(data.ph, data.pe, data.pl, data.pl, data.po)

message = data.combine_patterns(data.pko, data.pkha, data.pkyo, data.pku)

initialize()

clear()

try:

# Continue to display SMILE pattern and WINK pattern alternately

col = 0

while True:

t = DisplayThread(data.get_cycle_pattern(message, col))

t.start()

time.sleep(0.1)

t.stop()

col = col + 1 if col + 1 < len(message[0]) else 0

except KeyboardInterrupt:

# Before cleanup, it's needed to (1)stop the thread, (2)wait a bit.

# Otherwise, runtime error occurs requiring setmode.

t.stop()

time.sleep(0.1)

destroy()

概要

証明

斜め入射について

増加率一定

ロジスティック関数～増加に対する歯止め

パラメーターの影響

初期値N0

増加率r

収束値K

増加速度

概要

基本の枠組み

コード例

コードのモード確認

コードの配置

ブラウザ表示

HTML出力例

ASCII出力

UTF-8出力

HTML出力

ループの利用例

Apacheの設定

概要

VagrantのSSH設定内容確認

.ftpconfigの編集

接続開始と終了

電流・磁界の法則

右ネジの法則

右手の法則

フレミングの左手／右手の法則

ローレンツ力

レンツの法則

ファラデーの法則

コイルの自己誘導

自己誘導とは

電源が立ち上がった場合

電圧が立ち下がった場合

サージ

サージの考え方？

保護回路

概要

アクティブ・ブザー

単純接続

回路図

コード

パッシブ・ブザー

ソフトウェアによる音

PWMによる音

音階

音楽

バイポーラトランジスター

PNP型トランジスター

S8550トランジスター

概要

LCD1602

LCD1602のピン配置

表示領域～DDRAM

LCD1602のコマンド

8ビット/4ビットモードの設定

I2CによるLCD1602の制御

接続

LCDとRaspiの接続

初期手順

コード

動作テスト

文字表示

LCD1602クラス

概要

原理（マスターからスレーブへの書き込み）

ビットデータの転送

スタートコンディション／ストップコンディション

バイトデータの転送

スレーブアドレス送信とRW

ACK

I2Cの有効化

I2Cツール

i2cdetect

i2cdetect -V

i2cdetect -l

i2cdetect -F [bus]

初期値N₀