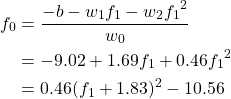MinMaxScaler

2020-10-04 / tau / コメントする

概要

sklearn.preprocessingモジュールのMinMaxScalerは、各特徴量が0～1の範囲に納まるように変換する。具体的には、特徴量F_iの最小値(min_i)と最大値(max_i)から以下の式により各特徴量F_iをF_i^*に変換する。

(1) $\begin{equation*} {F_i}^* = \frac{F_i - min_i}{max_i - min_i} \end{equation*}$

挙動

それぞれ異なる正規分布に従う2つの特徴量について、MinMaxScalerを適用したときの挙動を以下に示す。異なる大きさとレンジの特徴量が、変換後にはいずれも0～1の間に納まっているのが確認できる。

コードは以下の通りで、データに対してfit()メソッドでスケールパラメーターを決定し、transform()メソッドで変換を行うところを、これらを連続して実行するfit_transform()メソッドを使っている。

import numpy as np
import numpy.random as rnd
import matplotlib.pyplot as plt
from sklearn.preprocessing import MinMaxScaler

rnd.seed(0)
x1 = rnd.normal(loc=1, scale=1, size=100)
x2 = rnd.normal(loc=3, scale=0.5, size=100)
X = np.hstack((x1.reshape(-1, 1), x2.reshape(-1, 1)))

scaler = MinMaxScaler()
X_transformed = scaler.fit_transform(X)

fig = plt.figure(figsize=(9.6, 4.8))

ax1 = fig.add_subplot(2, 2, 1)
ax2 = fig.add_subplot(2, 2, 3)
ax3 = fig.add_subplot(1, 2, 2)

ax1.hist(X[:, 0], ec='k', range=(-2, 5), bins=40, alpha=0.5, label="Feature 0")
ax1.hist(X[:, 1], ec='k', range=(-2, 5), bins=40, alpha=0.5, label="Feature 1")
ax1.legend(loc='upper left')

ax2.hist(X_transformed[:, 0], range=(-0.2, 1.2), bins=40, ec='k', alpha=0.5,
    label="Feature 0")
ax2.hist(X_transformed[:, 1], range=(-0.2, 1.2), bins=40, ec='k', alpha=0.5,
    label="Feature 1")
ax2.legend(loc='upper left')

ax3.scatter(X[:, 0], X[:, 1], ec='k', fc='w', label="before transformation")
ax3.scatter(X_transformed[:, 0], X_transformed[:, 1], ec='k', fc='gray',
    label="after transformation")
ax3.set_aspect('equal')
ax3.set_xlim(-2, 5)
ax3.set_ylim(-2, 5)
ax3.set_xlabel("Feature 0")
ax3.set_ylabel("Feature 1")
ax3.legend()

plt.show()

import numpy as np

import numpy.random as rnd

import matplotlib.pyplot as plt

from sklearn.preprocessing import MinMaxScaler

rnd.seed(0)

x1 = rnd.normal(loc=1, scale=1, size=100)

x2 = rnd.normal(loc=3, scale=0.5, size=100)

X = np.hstack((x1.reshape(-1, 1), x2.reshape(-1, 1)))

scaler = MinMaxScaler()

X_transformed = scaler.fit_transform(X)

fig = plt.figure(figsize=(9.6, 4.8))

ax1 = fig.add_subplot(2, 2, 1)

ax2 = fig.add_subplot(2, 2, 3)

ax3 = fig.add_subplot(1, 2, 2)

ax1.hist(X[:, 0], ec='k', range=(-2, 5), bins=40, alpha=0.5, label="Feature 0")

ax1.hist(X[:, 1], ec='k', range=(-2, 5), bins=40, alpha=0.5, label="Feature 1")

ax1.legend(loc='upper left')

ax2.hist(X_transformed[:, 0], range=(-0.2, 1.2), bins=40, ec='k', alpha=0.5,

label="Feature 0")

ax2.hist(X_transformed[:, 1], range=(-0.2, 1.2), bins=40, ec='k', alpha=0.5,

label="Feature 1")

ax2.legend(loc='upper left')

ax3.scatter(X[:, 0], X[:, 1], ec='k', fc='w', label="before transformation")

ax3.scatter(X_transformed[:, 0], X_transformed[:, 1], ec='k', fc='gray',

label="after transformation")

ax3.set_aspect('equal')

ax3.set_xlim(-2, 5)

ax3.set_ylim(-2, 5)

ax3.set_xlabel("Feature 0")

ax3.set_ylabel("Feature 1")

ax3.legend()

plt.show()

特徴

MinMaxScalerは簡明な方法だが、極端に値が離れた異常値が発生すると本来のデータがその影響を受ける場合がある。

scikit-learn – predict_proba

2020-09-09 / tau / コメントする

概要

decision_function()は各データが推測したクラスに属する確信度(confidence)を表すが、超平面のパラメータに依存し、そのレンジや値の大きさと確信度の関係が明確ではない。

これに対してpredict_probaは、それぞれのターゲットが予測されたクラスに属する確率を0～1の実数で表す。2クラス分類では、結果の配列の形状は(n_sumples, 2)となる。

`predict_proba()`の挙動

以下はmake_circles()で生成した2クラスのデータをGradient Boostingによって分類したときの確信度。各データに対応した2要素の配列の1つ目がクラス0(blue)、2つ目がクラス1(orange)に属する確率を表し、2つの和は1となる。なお16行目でsuppress=Trueとすることで、ndarrayの表示を常に固定小数点としている。

import numpy as np
from sklearn.ensemble import GradientBoostingClassifier
from sklearn.datasets import make_circles
from sklearn.model_selection import train_test_split

X, y = make_circles(noise=0.25, factor=0.5, random_state=1)
y_named = np.array(["blue", "orange"])[y]

X_train, X_test, y_train, y_test, y_train_named, y_test_named = \
    train_test_split(X, y, y_named, random_state=0)

gbc = GradientBoostingClassifier(random_state=0)
gbc.fit(X_train, y_train_named)

pred_prob = gbc.predict_proba(X_test)
np.set_printoptions(suppress=True)
print(pred_prob)

# [[0.01573626 0.98426374]
#  [0.84575653 0.15424347]
#  [0.98112869 0.01887131]
#  .....
#  [0.06307595 0.93692405]
#  [0.93442475 0.06557525]
#  [0.86619957 0.13380043]]

import numpy as np

from sklearn.ensemble import GradientBoostingClassifier

from sklearn.datasets import make_circles

from sklearn.model_selection import train_test_split

X, y = make_circles(noise=0.25, factor=0.5, random_state=1)

y_named = np.array(["blue", "orange"])[y]

X_train, X_test, y_train, y_test, y_train_named, y_test_named = \

train_test_split(X, y, y_named, random_state=0)

gbc = GradientBoostingClassifier(random_state=0)

gbc.fit(X_train, y_train_named)

pred_prob = gbc.predict_proba(X_test)

np.set_printoptions(suppress=True)

print(pred_prob)

# [[0.01573626 0.98426374]

# [0.84575653 0.15424347]

# [0.98112869 0.01887131]

# .....

# [0.06307595 0.93692405]

# [0.93442475 0.06557525]

# [0.86619957 0.13380043]]

`decision_function()`との比較

先のコードに以下を続けて、predict_proba()による確率、予測されたクラス、decsion_function()の値と、各データの正解クラスを並べて表示する。予測されたクラスの方の確率が大きいこと、その予測結果とdecision_function()の符号が一致していることが確認できる。

prob0 = pred_prob[:, 0]
prob1 = pred_prob[:, 1]

data = DataFrame()
data["prob0"] = prob0
data["prob1"] = prob1
data["pred"] = gbc.predict(X_test)
data["dec_func"] = gbc.decision_function(X_test)
data["correct"] = y_test_named
print(data)

#        prob0     prob1    pred  dec_func correct
# 0   0.015736  0.984264  orange  4.135926  orange
# 1   0.845757  0.154243    blue -1.701699    blue
# 2   0.981129  0.018871    blue -3.951061    blue
# .....
# 22  0.063076  0.936924  orange  2.698263  orange
# 23  0.934425  0.065575    blue -2.656733    blue
# 24  0.866200  0.133800    blue -1.867766    blue

prob0 = pred_prob[:, 0]

prob1 = pred_prob[:, 1]

data = DataFrame()

data["prob0"] = prob0

data["prob1"] = prob1

data["pred"] = gbc.predict(X_test)

data["dec_func"] = gbc.decision_function(X_test)

data["correct"] = y_test_named

print(data)

# prob0 prob1 pred dec_func correct

# 0 0.015736 0.984264 orange 4.135926 orange

# 1 0.845757 0.154243 blue -1.701699 blue

# 2 0.981129 0.018871 blue -3.951061 blue

# .....

# 22 0.063076 0.936924 orange 2.698263 orange

# 23 0.934425 0.065575 blue -2.656733 blue

# 24 0.866200 0.133800 blue -1.867766 blue

このデータをクラス0(blue)に対する確率(prob0)でソートし、decision_function()との関係を見てみると、以下のことがわかる。

blueクラスの確率が高いとdecision_functionの確信度はマイナスで絶対値が大きくなり、orangeクラスの確率が高いと確信度はプラスで絶対値が大きくなる
blueクラスの確率とorangeクラスの確率が同程度の時、確信度の絶対値が同程度になり、符号が逆になる
確率に対して確信度は線形ではない

print(data.sort_values(by="prob0", ascending=False))

#        prob0     prob1    pred  dec_func correct
# 6   0.999543  0.000457    blue -7.690972    blue
# 10  0.998442  0.001558    blue -6.462560    blue
# 15  0.984817  0.015183    blue -4.172312  orange
# .....
# 0   0.015736  0.984264  orange  4.135926  orange
# 11  0.013521  0.986479  orange  4.289866  orange
# 4   0.013521  0.986479  orange  4.289866  orange

print(data.sort_values(by="prob0", ascending=False))

# prob0 prob1 pred dec_func correct

# 6 0.999543 0.000457 blue -7.690972 blue

# 10 0.998442 0.001558 blue -6.462560 blue

# 15 0.984817 0.015183 blue -4.172312 orange

# .....

# 0 0.015736 0.984264 orange 4.135926 orange

# 11 0.013521 0.986479 orange 4.289866 orange

# 4 0.013521 0.986479 orange 4.289866 orange

クラス0(blue)に対する確率とdecision_function()の確信度の関係を図示すると以下のようになり、確率に対して確信度が必ずしも線形になっていないことがわかる。

コードはmatplotlib.pyplotをインポートした上で、以下を追加。

prob = np.array(sorted_data["prob0"])
conf = np.array(sorted_data["dec_func"])
fig = plt.figure()
ax = fig.add_subplot()
ax.plot(prob, conf)
ax.grid()
ax.spines['top'].set_visible(False)
ax.spines['right'].set_visible(False)
ax.spines['bottom'].set_position('zero')
ax.spines['left'].set_position(('data', 0.5))
ax.set_xlabel("class-0 probaility", loc='left')
ax.set_ylabel("confidence", loc='bottom')
plt.show()

prob = np.array(sorted_data["prob0"])

conf = np.array(sorted_data["dec_func"])

fig = plt.figure()

ax = fig.add_subplot()

ax.plot(prob, conf)

ax.grid()

ax.spines['top'].set_visible(False)

ax.spines['right'].set_visible(False)

ax.spines['bottom'].set_position('zero')

ax.spines['left'].set_position(('data', 0.5))

ax.set_xlabel("class-0 probaility", loc='left')

ax.set_ylabel("confidence", loc='bottom')

plt.show()

決定境界

以下は、predict_proba()で計算された確率を可視化したもので、decision_function()の場合に比べて、直感的にも分かりやすい分布となっている。

コンターに表す値として、30行目でpredict_proba()の結果の0列目、すなわちClass0の確率を取り出している。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.ensemble import GradientBoostingClassifier
from sklearn.datasets import make_circles
from sklearn.model_selection import train_test_split

f0min, f0max = -1.5, 1.5
f1min, f1max = -1.75, 1.5

X, y = make_circles(noise=0.25, factor=0.5, random_state=1)

X_train, X_test, y_train, y_test =\
    train_test_split(X, y, random_state=0)

gb = GradientBoostingClassifier(random_state=0)
gb.fit(X_train, y_train)

fig, axs = plt.subplots(1, 2, figsize=(10, 4.8))
color0, color1 = 'tab:blue', 'tab:orange'

f0 = np.linspace(f0min, f0max, 200)
f1 = np.linspace(f1min, f1max, 200)
f0, f1 = np.meshgrid(f0, f1)
F = np.hstack((f0.reshape(-1, 1), f1.reshape(-1, 1)))

pred = gb.predict(F).reshape(f0.shape)
axs[0].contour(f0, f1, pred, levels=[0.5])
axs[0].contourf(f0, f1, pred, levels=1, colors=[color0, color1], alpha=0.25)

proba = gb.predict_proba(F)[:, 0].reshape(f0.shape)
print(proba.shape)
axs[1].contourf(f0, f1, proba, alpha=0.5, cmap='RdBu')

for ax in axs:
    ax.scatter(X_train[y_train==0][:, 0], X_train[y_train==0][:, 1], marker='o', fc=color0, ec='k', label="Train class 0")
    ax.scatter(X_test[y_test==0][:, 0], X_test[y_test==0][:, 1], marker='^', fc=color0, ec='k', label="Test Class 0")
    ax.scatter(X_train[y_train==1][:, 0], X_train[y_train==1][:, 1], marker='o', fc=color1, ec='k', label="Train class 1")
    ax.scatter(X_test[y_test==1][:, 0], X_test[y_test==1][:, 1], marker='^', fc=color1, ec='k', label="Test class 1")

    ax.set_xlim(f0min, f0max)
    ax.set_ylim(f1min, f1max)
    ax.tick_params(left=False, bottom=False, labelleft=False, labelbottom=False)

handles, labels = axs[0].get_legend_handles_labels()

fig.legend(handles, labels, ncol=4, loc='upper center')
plt.show()

import numpy as np

import matplotlib.pyplot as plt

from sklearn.ensemble import GradientBoostingClassifier

from sklearn.datasets import make_circles

from sklearn.model_selection import train_test_split

f0min, f0max = -1.5, 1.5

f1min, f1max = -1.75, 1.5

X, y = make_circles(noise=0.25, factor=0.5, random_state=1)

X_train, X_test, y_train, y_test =\

train_test_split(X, y, random_state=0)

gb = GradientBoostingClassifier(random_state=0)

gb.fit(X_train, y_train)

fig, axs = plt.subplots(1, 2, figsize=(10, 4.8))

color0, color1 = 'tab:blue', 'tab:orange'

f0 = np.linspace(f0min, f0max, 200)

f1 = np.linspace(f1min, f1max, 200)

f0, f1 = np.meshgrid(f0, f1)

F = np.hstack((f0.reshape(-1, 1), f1.reshape(-1, 1)))

pred = gb.predict(F).reshape(f0.shape)

axs[0].contour(f0, f1, pred, levels=[0.5])

axs[0].contourf(f0, f1, pred, levels=1, colors=[color0, color1], alpha=0.25)

proba = gb.predict_proba(F)[:, 0].reshape(f0.shape)

print(proba.shape)

axs[1].contourf(f0, f1, proba, alpha=0.5, cmap='RdBu')

for ax in axs:

ax.scatter(X_train[y_train==0][:, 0], X_train[y_train==0][:, 1], marker='o', fc=color0, ec='k', label="Train class 0")

ax.scatter(X_test[y_test==0][:, 0], X_test[y_test==0][:, 1], marker='^', fc=color0, ec='k', label="Test Class 0")

ax.scatter(X_train[y_train==1][:, 0], X_train[y_train==1][:, 1], marker='o', fc=color1, ec='k', label="Train class 1")

ax.scatter(X_test[y_test==1][:, 0], X_test[y_test==1][:, 1], marker='^', fc=color1, ec='k', label="Test class 1")

ax.set_xlim(f0min, f0max)

ax.set_ylim(f1min, f1max)

ax.tick_params(left=False, bottom=False, labelleft=False, labelbottom=False)

handles, labels = axs[0].get_legend_handles_labels()

fig.legend(handles, labels, ncol=4, loc='upper center')

plt.show()

3クラス以上の場合

3クラスのirisデータセットにGradientBoostingClassifierを適用し、predict_proba()の出力を見てみる。

import numpy as np
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.ensemble import GradientBoostingClassifier
from pandas import DataFrame

iris = load_iris()

X_train, X_test, y_train, y_test = train_test_split(
    iris.data, iris.target, random_state=42)

gbc = GradientBoostingClassifier(learning_rate=0.01, random_state=0)
gbc.fit(X_train, y_train)

pred_proba = gbc.predict_proba(X_test)
df = DataFrame(pred_proba, columns=iris.target_names)
df["decision"] = np.argmax(pred_proba, axis=1)
df["prediction"] = gbc.predict(X_test)
print(df)

import numpy as np

from sklearn.datasets import load_iris

from sklearn.model_selection import train_test_split

from sklearn.ensemble import GradientBoostingClassifier

from pandas import DataFrame

iris = load_iris()

X_train, X_test, y_train, y_test = train_test_split(

iris.data, iris.target, random_state=42)

gbc = GradientBoostingClassifier(learning_rate=0.01, random_state=0)

gbc.fit(X_train, y_train)

pred_proba = gbc.predict_proba(X_test)

df = DataFrame(pred_proba, columns=iris.target_names)

df["decision"] = np.argmax(pred_proba, axis=1)

df["prediction"] = gbc.predict(X_test)

print(df)

このコードの出力結果は以下の通り。3つのクラスに対する確率が得られ、合計は1になる。こちらはdecision_function()が2クラスの時だけ配列が1次元となるのと違って、どのような場合でも行数×列数＝データ数×クラス数の配列になる。

なお17行目で、argmaxを使って各データで確率が最大となるクラスを探している。

      setosa  versicolor  virginica  decision  prediction
0   0.102177    0.788400   0.109422         1           1
1   0.783471    0.109367   0.107161         0           0
2   0.098181    0.110059   0.791761         2           2
3   0.102177    0.788400   0.109422         1           1
4   0.103600    0.667239   0.229161         1           1
.....
33  0.783471    0.109367   0.107161         0           0
34  0.783471    0.109367   0.107161         0           0
35  0.101941    0.115024   0.783035         2           2
36  0.102177    0.788400   0.109422         1           1
37  0.783471    0.109367   0.107161         0           0

setosa versicolor virginica decision prediction

0 0.102177 0.788400 0.109422 1 1

1 0.783471 0.109367 0.107161 0 0

2 0.098181 0.110059 0.791761 2 2

3 0.102177 0.788400 0.109422 1 1

4 0.103600 0.667239 0.229161 1 1

.....

33 0.783471 0.109367 0.107161 0 0

34 0.783471 0.109367 0.107161 0 0

35 0.101941 0.115024 0.783035 2 2

36 0.102177 0.788400 0.109422 1 1

37 0.783471 0.109367 0.107161 0 0

scikit-learn – decision_function

2020-08-25 / tau / コメントする

概要

decision_function()は、超平面によってクラス分類をするモデルにおける、各予測データの確信度を表す。

2クラス分類の場合は(n_samples, )の1次元配列、マルチクラスの場合は(n_samples, n_classes)の2次元配列になる。2クラス分類の場合、符号の正負がそれぞれのクラスに対応する。

decision_function()を持つモデルは、LogisticRegression、SVC、GladientBoostClassifierなどで、RandomForestはこのメソッドを持っていない。

`decision_function()`の挙動

decision_function()の挙動をGradientBoostingClassifierで確認する。

まずmake_circles()で2クラスのデータを生成し、外側のクラス0をblue、内側のクラス1をorangeとして再定義する。

import numpy as np
from sklearn.ensemble import GradientBoostingClassifier
from sklearn.datasets import make_circles
from sklearn.model_selection import train_test_split

X, y = make_circles(noise=0.25, factor=0.5, random_state=1)
y_named = np.array(["blue", "orange"])[y]

import numpy as np

from sklearn.ensemble import GradientBoostingClassifier

from sklearn.datasets import make_circles

from sklearn.model_selection import train_test_split

X, y = make_circles(noise=0.25, factor=0.5, random_state=1)

y_named = np.array(["blue", "orange"])[y]

次に、データを訓練データとテストデータに分割し、訓練データによって学習する。データ分割にあたって、Xとyに加えて文字列に置き換えたy_namedを分割している。学習の際にはXとy_namedの訓練データとテストデータのみを用いるのでyについては特に含める必要ないが、ここではtrain_test_split()が3つ以上のデータでも分割可能なことを示している。

X_train, X_test, y_train, y_test, y_train_named, y_test_named = \
    train_test_split(X, y, y_named, random_state=0)

gbc = GradientBoostingClassifier(random_state=0)
gbc.fit(X_train, y_train_named)

X_train, X_test, y_train, y_test, y_train_named, y_test_named = \

train_test_split(X, y, y_named, random_state=0)

gbc = GradientBoostingClassifier(random_state=0)

gbc.fit(X_train, y_train_named)

学習後の分類器のclasses_プロパティーを参照すると、クラスがどのように表現されるかを確認できる。上のfit()メソッドでy_train_namedを与えたのでクラスの表現が文字列になっているが、代わりにy_trainを用いると[0, 1]のように元のyに対応したクラス表現が返される。

print(gbc.classes_)

# ['blue' 'orange']

print(gbc.classes_)

# ['blue' 'orange']

次に、学習済みモデルにテストデータを与えて、decision_function()の結果とpredict()の結果を並べてみる。decision_function()はfit()で与えたテストデータ数の1次元配列を返し、各要素の負の値に対してクラス0のblueが、正の値に対してはクラス1のorangeがpredict()で予測されていることがわかる。

data = DataFrame()
data["decision_value"] = gbc.decision_function(X_test)
data["prediction"] = gbc.predict(X_test)
print(data)

#     decision_value prediction
# 0         4.135926     orange
# 1        -1.701699       blue
# 2        -3.951061       blue
# 3        -3.626096       blue
# 4         4.289866     orange
# 5         3.661661     orange
# 6        -7.690972       blue
# 7         4.110017     orange
# 8         1.107539     orange
# 9         3.407822     orange
# 10       -6.462560       blue
# 11        4.289866     orange
# 12        3.901563     orange
# 13       -1.200312       blue
# 14        3.661661     orange
# 15       -4.172312       blue
# 16       -1.230101       blue
# 17       -3.915762       blue
# 18        4.036028     orange
# 19        4.110017     orange
# 20        4.110017     orange
# 21        0.657090     orange
# 22        2.698263     orange
# 23       -2.656733       blue
# 24       -1.867766       blue

data = DataFrame()

data["decision_value"] = gbc.decision_function(X_test)

data["prediction"] = gbc.predict(X_test)

print(data)

# decision_value prediction

# 0 4.135926 orange

# 1 -1.701699 blue

# 2 -3.951061 blue

# 3 -3.626096 blue

# 4 4.289866 orange

# 5 3.661661 orange

# 6 -7.690972 blue

# 7 4.110017 orange

# 8 1.107539 orange

# 9 3.407822 orange

# 10 -6.462560 blue

# 11 4.289866 orange

# 12 3.901563 orange

# 13 -1.200312 blue

# 14 3.661661 orange

# 15 -4.172312 blue

# 16 -1.230101 blue

# 17 -3.915762 blue

# 18 4.036028 orange

# 19 4.110017 orange

# 20 4.110017 orange

# 21 0.657090 orange

# 22 2.698263 orange

# 23 -2.656733 blue

# 24 -1.867766 blue

decision_function()の各要素の符号に応じてpredict()と同じ結果を得たいなら、次のように処理していくとよい。

print(gbc.decision_function(X_test) > 0)
# [ True False False False  True  True False  True  True  True False  True
#   True False  True False False False  True  True  True  True  True False
#  False]

print((gbc.decision_function(X_test) > 0).astype(int))
# [1 0 0 0 1 1 0 1 1 1 0 1 1 0 1 0 0 0 1 1 1 1 1 0 0]

print(gbc.classes_[(gbc.decision_function(X_test) > 0).astype(int)])
# ['orange' 'blue' 'blue' 'blue' 'orange' 'orange' 'blue' 'orange' 'orange'
#  'orange' 'blue' 'orange' 'orange' 'blue' 'orange' 'blue' 'blue' 'blue'
#  'orange' 'orange' 'orange' 'orange' 'orange' 'blue' 'blue']

print(gbc.decision_function(X_test) > 0)

# [ True False False False True True False True True True False True

# True False True False False False True True True True True False

# False]

print((gbc.decision_function(X_test) > 0).astype(int))

# [1 0 0 0 1 1 0 1 1 1 0 1 1 0 1 0 0 0 1 1 1 1 1 0 0]

print(gbc.classes_[(gbc.decision_function(X_test) > 0).astype(int)])

# ['orange' 'blue' 'blue' 'blue' 'orange' 'orange' 'blue' 'orange' 'orange'

# 'orange' 'blue' 'orange' 'orange' 'blue' 'orange' 'blue' 'blue' 'blue'

# 'orange' 'orange' 'orange' 'orange' 'orange' 'blue' 'blue']

最後に、上記のデータと正解であるy_test_namedのデータを先ほどのデータフレームに追加して全体を確認する。predit()メソッドの結果とdecision_function()の符号による判定結果は等しく、y_testと異なるデータがあることがわかる。

data["decision"] = \
    gbc.classes_[(gbc.decision_function(X_test) > 0).astype(int)]
data["y_test"] = y_test_named

print(data)

#     decision_value prediction decision  y_test
# 0         4.135926     orange   orange  orange
# 1        -1.701699       blue     blue    blue
# 2        -3.951061       blue     blue    blue
# 3        -3.626096       blue     blue    blue
# 4         4.289866     orange   orange  orange
# 5         3.661661     orange   orange  orange
# 6        -7.690972       blue     blue    blue
# 7         4.110017     orange   orange  orange
# 8         1.107539     orange   orange  orange
# 9         3.407822     orange   orange  orange
# 10       -6.462560       blue     blue    blue
# 11        4.289866     orange   orange  orange
# 12        3.901563     orange   orange  orange
# 13       -1.200312       blue     blue  orange
# 14        3.661661     orange   orange  orange
# 15       -4.172312       blue     blue  orange
# 16       -1.230101       blue     blue  orange
# 17       -3.915762       blue     blue    blue
# 18        4.036028     orange   orange  orange
# 19        4.110017     orange   orange  orange
# 20        4.110017     orange   orange    blue
# 21        0.657090     orange   orange  orange
# 22        2.698263     orange   orange  orange
# 23       -2.656733       blue     blue    blue
# 24       -1.867766       blue     blue    blue

data["decision"] = \

gbc.classes_[(gbc.decision_function(X_test) > 0).astype(int)]

data["y_test"] = y_test_named

print(data)

# decision_value prediction decision y_test

# 0 4.135926 orange orange orange

# 1 -1.701699 blue blue blue

# 2 -3.951061 blue blue blue

# 3 -3.626096 blue blue blue

# 4 4.289866 orange orange orange

# 5 3.661661 orange orange orange

# 6 -7.690972 blue blue blue

# 7 4.110017 orange orange orange

# 8 1.107539 orange orange orange

# 9 3.407822 orange orange orange

# 10 -6.462560 blue blue blue

# 11 4.289866 orange orange orange

# 12 3.901563 orange orange orange

# 13 -1.200312 blue blue orange

# 14 3.661661 orange orange orange

# 15 -4.172312 blue blue orange

# 16 -1.230101 blue blue orange

# 17 -3.915762 blue blue blue

# 18 4.036028 orange orange orange

# 19 4.110017 orange orange orange

# 20 4.110017 orange orange blue

# 21 0.657090 orange orange orange

# 22 2.698263 orange orange orange

# 23 -2.656733 blue blue blue

# 24 -1.867766 blue blue blue

`decision_function()`の意味

decusuib_function()のレベルは超平面上の高さになるが、これはデータ、モデルパラメーターにより変化し、このスケールの解釈は難しい。それはpredict_proba()で得られる予測確率とdecision_function()で計算される確信度の非線形性からも予想される。

circlesデータに対するGradientBoostingClassifierの決定境界とdecision_function()の値の分布を表示したのが以下の図。コンターが交錯していてわかりにくく、直感的にはpredict_proba()の方がわかりやすい。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_circles
from sklearn.model_selection import train_test_split
from sklearn.ensemble import GradientBoostingClassifier

f0min, f0max = -1.5, 1.5
f1min, f1max = -1.75, 1.5

X, y = make_circles(noise=0.25, factor=0.5, random_state=1)

X_train, X_test, y_train, y_test =\
    train_test_split(X, y, random_state=0)

gb = GradientBoostingClassifier(random_state=0)

gb.fit(X_train, y_train)

print("X_test.shape           : {}".format(X_test.shape))
print("Decision function shape: {}".format(
    gb.decision_function(X_test).shape))

fig, axs = plt.subplots(1, 2, figsize=(10, 4.8))
color0, color1 = 'tab:blue', 'tab:orange'

f0 = np.linspace(f0min, f0max, 200)
f1 = np.linspace(f1min, f1max, 200)
f0, f1 = np.meshgrid(f0, f1)
F = np.c_[f0.reshape(-1, 1), f1.reshape(-1, 1)]

pred = gb.predict(F).reshape(f0.shape)
axs[0].contour(f0, f1, pred, levels=[0.5])
axs[0].contourf(f0, f1, pred, levels=1, colors=[color0, color1], alpha=0.25)

decision = gb.decision_function(F).reshape(f0.shape)
axs[1].contourf(f0, f1, decision, alpha=0.5, cmap='bwr')

for ax in axs:
    ax.scatter(X_train[y_train==0][:, 0], X_train[y_train==0][:, 1], marker='o', fc=color0, ec='k', label="Train class 0")
    ax.scatter(X_test[y_test==0][:, 0], X_test[y_test==0][:, 1], marker='^', fc=color0, ec='k', label="Test Class 0")
    ax.scatter(X_train[y_train==1][:, 0], X_train[y_train==1][:, 1], marker='o', fc=color1, ec='k', label="Train class 1")
    ax.scatter(X_test[y_test==1][:, 0], X_test[y_test==1][:, 1], marker='^', fc=color1, ec='k', label="Test class 1")

    ax.set_xlim(f0min, f0max)
    ax.set_ylim(f1min, f1max)
    ax.tick_params(left=False, bottom=False, labelleft=False, labelbottom=False)

handles, labels = axs[0].get_legend_handles_labels()

fig.legend(handles, labels, ncol=4, loc='upper center')
plt.show()

import numpy as np

import matplotlib.pyplot as plt

from sklearn.datasets import make_circles

from sklearn.model_selection import train_test_split

from sklearn.ensemble import GradientBoostingClassifier

f0min, f0max = -1.5, 1.5

f1min, f1max = -1.75, 1.5

X, y = make_circles(noise=0.25, factor=0.5, random_state=1)

X_train, X_test, y_train, y_test =\

train_test_split(X, y, random_state=0)

gb = GradientBoostingClassifier(random_state=0)

gb.fit(X_train, y_train)

print("X_test.shape : {}".format(X_test.shape))

print("Decision function shape: {}".format(

gb.decision_function(X_test).shape))

fig, axs = plt.subplots(1, 2, figsize=(10, 4.8))

color0, color1 = 'tab:blue', 'tab:orange'

f0 = np.linspace(f0min, f0max, 200)

f1 = np.linspace(f1min, f1max, 200)

f0, f1 = np.meshgrid(f0, f1)

F = np.c_[f0.reshape(-1, 1), f1.reshape(-1, 1)]

pred = gb.predict(F).reshape(f0.shape)

axs[0].contour(f0, f1, pred, levels=[0.5])

axs[0].contourf(f0, f1, pred, levels=1, colors=[color0, color1], alpha=0.25)

decision = gb.decision_function(F).reshape(f0.shape)

axs[1].contourf(f0, f1, decision, alpha=0.5, cmap='bwr')

for ax in axs:

ax.scatter(X_train[y_train==0][:, 0], X_train[y_train==0][:, 1], marker='o', fc=color0, ec='k', label="Train class 0")

ax.scatter(X_test[y_test==0][:, 0], X_test[y_test==0][:, 1], marker='^', fc=color0, ec='k', label="Test Class 0")

ax.scatter(X_train[y_train==1][:, 0], X_train[y_train==1][:, 1], marker='o', fc=color1, ec='k', label="Train class 1")

ax.scatter(X_test[y_test==1][:, 0], X_test[y_test==1][:, 1], marker='^', fc=color1, ec='k', label="Test class 1")

ax.set_xlim(f0min, f0max)

ax.set_ylim(f1min, f1max)

ax.tick_params(left=False, bottom=False, labelleft=False, labelbottom=False)

handles, labels = axs[0].get_legend_handles_labels()

fig.legend(handles, labels, ncol=4, loc='upper center')

plt.show()

3クラス以上の場合

3クラスのirisデータセットにGradientBoostingClassifierを適用して、decision_function()の出力を見てみる。

import numpy as np
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.ensemble import GradientBoostingClassifier
from pandas import DataFrame

iris = load_iris()

X_train, X_test, y_train, y_test = train_test_split(
    iris.data, iris.target, random_state=42)

gbc = GradientBoostingClassifier(learning_rate=0.01, random_state=0)
gbc.fit(X_train, y_train)

dec_func = gbc.decision_function(X_test)
print(dec_func.shape)
df = DataFrame(dec_func, columns=iris.target_names)

df["decision"] = np.argmax(dec_func, axis=1)
df["prediction"] = gbc.predict(X_test)
print(df)

import numpy as np

from sklearn.datasets import load_iris

from sklearn.model_selection import train_test_split

from sklearn.ensemble import GradientBoostingClassifier

from pandas import DataFrame

iris = load_iris()

X_train, X_test, y_train, y_test = train_test_split(

iris.data, iris.target, random_state=42)

gbc = GradientBoostingClassifier(learning_rate=0.01, random_state=0)

gbc.fit(X_train, y_train)

dec_func = gbc.decision_function(X_test)

print(dec_func.shape)

df = DataFrame(dec_func, columns=iris.target_names)

df["decision"] = np.argmax(dec_func, axis=1)

df["prediction"] = gbc.predict(X_test)

print(df)

このコードの出力結果は以下の通り。2クラスの場合は1次元配列だったが、3クラスになると行数×列数がデータ数×クラス数の配列になる。predict_proba()は2クラスでも2列の配列になるので、decision_function()の2クラスの場合だけ特に1次元配列になると言える。

なお、19行目で各データごとに最大の値をとる列をargmaxで探して、そのサフィックスを”decision”のクラス番号として表示している。

(38, 3)
      setosa  versicolor  virginica  decision  prediction
0  -1.995715    0.047583  -1.927207         1           1
1   0.061464   -1.907557  -1.927938         0           0
2  -1.990582   -1.876379   0.096867         2           2
3  -1.995715    0.047583  -1.927207         1           1
4  -1.997302   -0.134691  -1.203415         1           1
.....
33  0.061464   -1.907557  -1.927938         0           0
34  0.061464   -1.907557  -1.927938         0           0
35 -1.997122   -1.876379   0.041660         2           2
36 -1.995715    0.047583  -1.927207         1           1
37  0.061464   -1.907557  -1.927938         0           0

(38, 3)

setosa versicolor virginica decision prediction

0 -1.995715 0.047583 -1.927207 1 1

1 0.061464 -1.907557 -1.927938 0 0

2 -1.990582 -1.876379 0.096867 2 2

3 -1.995715 0.047583 -1.927207 1 1

4 -1.997302 -0.134691 -1.203415 1 1

.....

33 0.061464 -1.907557 -1.927938 0 0

34 0.061464 -1.907557 -1.927938 0 0

35 -1.997122 -1.876379 0.041660 2 2

36 -1.995715 0.047583 -1.927207 1 1

37 0.061464 -1.907557 -1.927938 0 0

scikit-learn – make_circles

2020-08-23 / tau / コメントする

概要

sklearn.datasets.make_circles()はクラス分類のためのデータを生成する。2つのクラスのデータが同心円状に分布し、各クラスの半径の差異、データのばらつきを指定できる。

得られるデータの形式

2つの配列X, yが返され、配列Xは列が特徴量、行がレコードの2次元配列。ターゲットyはレコード数分のクラス属性値の整数で0か1の値をとる。

from sklearn.datasets import make_circles

X, y = make_circles(n_samples=10, random_state=0)

print("X:\n{}".format(X))
print("y:{}".format(y))

# X:
# [[-0.80901699  0.58778525]
#  [-0.6472136  -0.4702282 ]
#  [ 0.30901699 -0.95105652]
#  [ 0.2472136  -0.76084521]
#  [ 0.30901699  0.95105652]
#  [ 0.2472136   0.76084521]
#  [-0.6472136   0.4702282 ]
#  [-0.80901699 -0.58778525]
#  [ 1.          0.        ]
#  [ 0.8         0.        ]]
# y:[0 1 0 1 0 1 1 0 0 1]

from sklearn.datasets import make_circles

X, y = make_circles(n_samples=10, random_state=0)

print("X:\n{}".format(X))

print("y:{}".format(y))

# X:

# [[-0.80901699 0.58778525]

# [-0.6472136 -0.4702282 ]

# [ 0.30901699 -0.95105652]

# [ 0.2472136 -0.76084521]

# [ 0.30901699 0.95105652]

# [ 0.2472136 0.76084521]

# [-0.6472136 0.4702282 ]

# [-0.80901699 -0.58778525]

# [ 1. 0. ]

# [ 0.8 0. ]]

# y:[0 1 0 1 0 1 1 0 0 1]

パラメーターの指定

sklearn.datasets.make_circles(n_samples=100, *, shuffle=True, noise=None, random_state=None, factor=0.8)

1	sklearn.datasets.make_circles(n_samples=100, *, shuffle=True, noise=None, random_state=None, factor=0.8)

n_samples: 総データ数で、奇数の場合は内側のデータが1つ多くなる。2要素のタプルで指定した場合、1つ目が外側、2つ目が内側のデータ数となる。デフォルトは100
shuffle: データをシャッフルするかどうかを指定。Falseにすると、前半がクラス0、後半がクラス1となるように並ぶ。デフォルトはTrue。
noise: ガウス分布のノイズを標準偏差で指定。デフォルトはNoneでノイズなし。
random_state: データを生成する乱数系列を指定。デフォルトはNone
factor: 外側に対する内側のデータのスケールファクター。デフォルトは0.8。

利用例

以下はスケールファクターを0.5、ノイズを0.15としてデフォルトの100個のデータを生成した例。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_circles

X, y = make_circles(factor=0.5, noise=0.15)

X0 = X[y==0]
X1 = X[y==1]

fig, ax = plt.subplots()
ax.scatter(X0[:, 0], X0[:, 1])
ax.scatter(X1[:, 0], X1[:, 1])

plt.show()

import numpy as np

import matplotlib.pyplot as plt

from sklearn.datasets import make_circles

X, y = make_circles(factor=0.5, noise=0.15)

X0 = X[y==0]

X1 = X[y==1]

fig, ax = plt.subplots()

ax.scatter(X0[:, 0], X0[:, 1])

ax.scatter(X1[:, 0], X1[:, 1])

plt.show()

以下はノイズの程度を変化させた例。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_circles

scale_factors = [0, 0.4, 0.6, 0.8]

fig = plt.figure(figsize=(9.6,7.2))
axs = fig.subplots(2, 2)

for ax, factor in zip(axs.reshape(axs.size), scale_factors):
    X, y = make_circles(noise=0.1, factor=factor, random_state=0)

    ax.scatter(X[y==0][:, 0], X[y==0][:, 1])
    ax.scatter(X[y==1][:, 0], X[y==1][:, 1])
    ax.set_title("factor={:3.1f}".format(factor))

fig.subplots_adjust(wspace=0.3, hspace=0.4)

plt.show()

import numpy as np

import matplotlib.pyplot as plt

from sklearn.datasets import make_circles

scale_factors = [0, 0.4, 0.6, 0.8]

fig = plt.figure(figsize=(9.6,7.2))

axs = fig.subplots(2, 2)

for ax, factor in zip(axs.reshape(axs.size), scale_factors):

X, y = make_circles(noise=0.1, factor=factor, random_state=0)

ax.scatter(X[y==0][:, 0], X[y==0][:, 1])

ax.scatter(X[y==1][:, 0], X[y==1][:, 1])

ax.set_title("factor={:3.1f}".format(factor))

fig.subplots_adjust(wspace=0.3, hspace=0.4)

plt.show()

以下はスケールファクターを変化させた例。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_circles

scale_factors = [0, 0.4, 0.6, 0.8]

fig = plt.figure(figsize=(9.6,7.2))
axs = fig.subplots(2, 2)

for ax, factor in zip(axs.reshape(axs.size), scale_factors):
    X, y = make_circles(noise=0.1, factor=factor, random_state=0)

    ax.scatter(X[y==0][:, 0], X[y==0][:, 1])
    ax.scatter(X[y==1][:, 0], X[y==1][:, 1])
    ax.set_title("factor={:3.1f}".format(factor))

fig.subplots_adjust(wspace=0.3, hspace=0.4)

plt.show()

import numpy as np

import matplotlib.pyplot as plt

from sklearn.datasets import make_circles

scale_factors = [0, 0.4, 0.6, 0.8]

fig = plt.figure(figsize=(9.6,7.2))

axs = fig.subplots(2, 2)

for ax, factor in zip(axs.reshape(axs.size), scale_factors):

X, y = make_circles(noise=0.1, factor=factor, random_state=0)

ax.scatter(X[y==0][:, 0], X[y==0][:, 1])

ax.scatter(X[y==1][:, 0], X[y==1][:, 1])

ax.set_title("factor={:3.1f}".format(factor))

fig.subplots_adjust(wspace=0.3, hspace=0.4)

plt.show()

MLP – 多層パーセプトロン

2020-07-04 / tau / コメントする

線形モデルの多層化

“Pythonではじめる機械学習”の写経。多層パーセプトロン(Multilayer perceptron : MLP)はフィードフォワード・ニューラルネットワークとも呼ばれる。

まず、線形モデルを以下の式で表す。

(1) $\begin{equation*} b + w_0 x_0 + \cdots + w_n x_n \end{equation*}$

n = 3の場合について図示すると、以下のように表せる。左側のノードの特徴量x_iに対して、w_iによる重み付き和を計算している。

MLPは、この構造に中間層を導入し、中間層に隠れユニット(hidden units)を配置する。特徴量入力はまず隠れユニットに対して重み付き線形和を計算し、その後に隠れユニットの出力の重み付き線形和を出力とする。

特徴量x_i (i = 0～n)の隠れユニットh_j (j = 0～m)に対する重みをw_ij、切片をb_jとすると、h_jへの入力となる重み付き線形和は以下のようになる。

(2) $\begin{equation*} h_j = \sum_{i=0}^n (b_j + w_{ij} x_i) \end{equation*}$

また、隠れユニットh_jの出力 $\hat{y}$ に対する重みをv_j、切片をcとすると、出力への重み付き線形和は以下のようになる。

(3) $\begin{equation*} \hat{y} = c + \sum_{j=0}^m v_j h_j = c + \sum_{j=0}^m v_j \sum_{i=0}^n (b_{ij} + w_{0ij} x_i) \end{equation*}$

これは結局、xiに対する重み付き線形和となる。たとえば特徴量0～3、隠れユニット0～2の場合は以下のとおり。

(4) $\begin{align*} \hat{y} &= c + v_0 h_0 + v_1 h_1 + v_2 h_2 \\ &= c + v_0 (b_0 + w_{00} x_0 + w_{10} x_1 + w_{20} x_2) \\ &\phantom{=c+}v_1 (b_1 + w_{01} x_0 + w_{11} x_1 + w_{21} x_2) \\ &\phantom{=c+}v_2 (b_2 + w_{02} x_0 + w_{12} x_1 + w_{22} x_2) \\ &= c + v_0 b_0 + v_1 b_1 + v_2 b_2 \\ &\phantom{=}+ (v_0 w_{00} + v_1 w_{01} + v_2 w_{02}) x_0 \\ &\phantom{=}+ (v_0 w_{10} + v_1 w_{11} + v_2 w_{12}) x_1 \\ &\phantom{=}+ (v_0 w_{20} + v_1 w_{21} + v_2 w_{22}) x_2 \end{align*}$

非線形活性化関数

単純な線形和をいくら多層化しても、結果は特徴量の線形和にしかならない。そこで、隠れユニットの入力に対して非線形関数を適用して出力とし、複雑・柔軟な動作を可能とする。

このような関数を活性化関数(activation function)あるいは伝達関数(transfer function)と呼び、様々な種類がある。書籍では、このうちReLU (Rectified linear unit)とtanh (hyperbolic tangent)が紹介されている。ReLUは以下の式で表され、負の値が採用しえない（計算過程での）ノイズであるような場合に好都合らしい。tanhは(−∞, +∞)の入力に対して(−1, +1)の出力を返す。

(5) $\begin{equation*} h(x) = \max (0, x) = \left\{ \begin{align} x \quad (x \ge 0) \\ 0 \quad(x < 0) \end{aling} \right. \end{equation*}$

import numpy as np
import matplotlib.pyplot as plt

xmin, xmax = -5, 5
ymin, ymax = -1, 3
x = np.linspace(xmin, xmax, 100)
tanh = np.tanh(x)
relu = np.maximum(x, 0)

fig, ax = plt.subplots()
ax.plot(x, tanh, label="tanh", linewidth=2,)
ax.plot(x, relu, label="relu", linewidth=2, linestyle='dashed')
ax.set_xlim(xmin, xmax)
ax.set_ylim(ymin, ymax)
ax.set_xlabel("x")
ax.set_ylabel("tanh, relu")
ax.grid(True)
ax.legend()
plt.show()

import numpy as np

import matplotlib.pyplot as plt

xmin, xmax = -5, 5

ymin, ymax = -1, 3

x = np.linspace(xmin, xmax, 100)

tanh = np.tanh(x)

relu = np.maximum(x, 0)

fig, ax = plt.subplots()

ax.plot(x, tanh, label="tanh", linewidth=2,)

ax.plot(x, relu, label="relu", linewidth=2, linestyle='dashed')

ax.set_xlim(xmin, xmax)

ax.set_ylim(ymin, ymax)

ax.set_xlabel("x")

ax.set_ylabel("tanh, relu")

ax.grid(True)

ax.legend()

plt.show()

ニューラルネットワークのチューニング

two moonsデータでの確認

two moonsデータセットに対してMLPを適用する。隠れユニットの数はデフォルトの100としている。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_moons
from sklearn.model_selection import train_test_split
from sklearn.neural_network import MLPClassifier

xmin, xmax = -1.5, 2.5
ymin, ymax = -0.75, 1.75

X, y = make_moons(n_samples=100, noise=0.25, random_state=3)
X_train, X_test, y_train, y_test = \
    train_test_split(X, y, stratify=y, random_state=42)

mlp = MLPClassifier(solver='lbfgs', random_state=0).fit(X_train, y_train)

f0 = np.linspace(xmin, xmax, 400)
f1 = np.linspace(ymin, ymax, 400)
f0, f1 = np.meshgrid(f0, f1)
pred = mlp.predict(np.vstack([f0.ravel(), f1.ravel()]).T).reshape(f0.shape)

fig, ax = plt.subplots()
color0, color1 = 'tab:blue', 'tab:orange'
Xtr0 = X_train[y_train==0]
Xtr1 = X_train[y_train==1]
ax.scatter(Xtr0[:, 0], Xtr0[:, 1], marker='o', s=80, color=color0)
ax.scatter(Xtr1[:, 0], Xtr1[:, 1], marker='^', s=80, color=color1)
ax.contourf(f0, f1, pred, levels=1, colors=[color0, color1], alpha=0.25)
ax.contour(f0, f1, pred, levels=[0.5])
ax.set_xlim(xmin, xmax)
ax.set_ylim(ymin, ymax)
ax.set_xlabel("Feature 0")
ax.set_ylabel("Feature 1")
plt.show()

import numpy as np

import matplotlib.pyplot as plt

from sklearn.datasets import make_moons

from sklearn.model_selection import train_test_split

from sklearn.neural_network import MLPClassifier

xmin, xmax = -1.5, 2.5

ymin, ymax = -0.75, 1.75

X, y = make_moons(n_samples=100, noise=0.25, random_state=3)

X_train, X_test, y_train, y_test = \

train_test_split(X, y, stratify=y, random_state=42)

mlp = MLPClassifier(solver='lbfgs', random_state=0).fit(X_train, y_train)

f0 = np.linspace(xmin, xmax, 400)

f1 = np.linspace(ymin, ymax, 400)

f0, f1 = np.meshgrid(f0, f1)

pred = mlp.predict(np.vstack([f0.ravel(), f1.ravel()]).T).reshape(f0.shape)

fig, ax = plt.subplots()

color0, color1 = 'tab:blue', 'tab:orange'

Xtr0 = X_train[y_train==0]

Xtr1 = X_train[y_train==1]

ax.scatter(Xtr0[:, 0], Xtr0[:, 1], marker='o', s=80, color=color0)

ax.scatter(Xtr1[:, 0], Xtr1[:, 1], marker='^', s=80, color=color1)

ax.contourf(f0, f1, pred, levels=1, colors=[color0, color1], alpha=0.25)

ax.contour(f0, f1, pred, levels=[0.5])

ax.set_xlim(xmin, xmax)

ax.set_ylim(ymin, ymax)

ax.set_xlabel("Feature 0")

ax.set_ylabel("Feature 1")

plt.show()

隠れユニット数と決定境界

隠れユニット数を10とした場合の結果は数の通り。先のユニット数100の場合に比べて、決定境界が折れ線になっている。

隠れユニット数の指定はhidden_layer_sizes=[10]のように指定する。複数の隠れ層を表現するためにリストとなっていて、1層の場合でも1要素のリストとする。また、収束計算回数の最大値がデフォルトのmax_iter=200では収束しきれないという警告が出るため、この値を1000に引き上げている。

結果は書籍のものと少し異なっていて、上方の▲の点より上に鋭く境界が突き抜けている。いくつかパラメーターを変えてみたが、書籍のような境界の形状は再現できなかった。

mlp = MLPClassifier(solver='lbfgs', random_state=0,
    hidden_layer_sizes=[10], max_iter=1000).fit(X_train, y_train)

1 2	mlp = MLPClassifier(solver='lbfgs', random_state=0, hidden_layer_sizes=[10], max_iter=1000).fit(X_train, y_train)

隠れユニットの数を[1]～[4]と変化させたときの決定境界の様子は以下の通りで、ユニット数が増えるにしたがって決定境界を構成する線分の数が増えている。

for i, ax in enumerate(axs.reshape(-1)):
    ax.scatter(Xtr0[:, 0], Xtr0[:, 1], marker='o', s=40, color=color0)
    ax.scatter(Xtr1[:, 0], Xtr1[:, 1], marker='^', s=40, color=color1)

    mlp = MLPClassifier(solver='lbfgs', random_state=0,
        hidden_layer_sizes=[i+1]).fit(X_train, y_train)
    pred = mlp.predict(np.vstack([f0.ravel(), f1.ravel()]).T).reshape(f0.shape)
    ax.contourf(f0, f1, pred, levels=1, colors=[color0, color1], alpha=0.25)
    ax.contour(f0, f1, pred, levels=[0.5])

    ax.set_xlim(xmin, xmax)
    ax.set_ylim(ymin, ymax)
    ax.tick_params(bottom=False, left=False, labelbottom=False, labelleft=False)
    ax.set_title("hidden_units={}".format(i + 1))
plt.show()

for i, ax in enumerate(axs.reshape(-1)):

ax.scatter(Xtr0[:, 0], Xtr0[:, 1], marker='o', s=40, color=color0)

ax.scatter(Xtr1[:, 0], Xtr1[:, 1], marker='^', s=40, color=color1)

mlp = MLPClassifier(solver='lbfgs', random_state=0,

hidden_layer_sizes=[i+1]).fit(X_train, y_train)

pred = mlp.predict(np.vstack([f0.ravel(), f1.ravel()]).T).reshape(f0.shape)

ax.contourf(f0, f1, pred, levels=1, colors=[color0, color1], alpha=0.25)

ax.contour(f0, f1, pred, levels=[0.5])

ax.set_xlim(xmin, xmax)

ax.set_ylim(ymin, ymax)

ax.tick_params(bottom=False, left=False, labelbottom=False, labelleft=False)

ax.set_title("hidden_units={}".format(i + 1))

plt.show()

隠れ層の数

隠れユニット数が10程度でも、隠れ層の数を増やすと決定境界は滑らかになる。

mlp = MLPClassifier(solver='lbfgs', random_state=0,
    hidden_layer_sizes=[10, 10]).fit(X_train, y_train)

1 2	mlp = MLPClassifier(solver='lbfgs', random_state=0, hidden_layer_sizes=[10, 10]).fit(X_train, y_train)

隠れ層が2層の場合に、各層のユニット数を変化させたときの決定境界の変化を見てみる。1層目のユニット数が大まかな形に影響し、2層目のユニットは決定境界の滑らかさに影響していると言えそうだ。

units0_list = [1, 5, 10]
units1_list = [1, 5, 10]
for row, units0 in enumerate(units0_list):
    for col, units1 in enumerate(units1_list):
        ax = axs[row, col]
        ax.scatter(Xtr0[:, 0], Xtr0[:, 1], marker='o', s=20, color=color0)
        ax.scatter(Xtr1[:, 0], Xtr1[:, 1], marker='^', s=20, color=color1)

        mlp = MLPClassifier(solver='lbfgs', random_state=0,
            hidden_layer_sizes=[units0, units1]).fit(X_train, y_train)
        pred = mlp.predict(np.vstack([f0.ravel(), f1.ravel()]).T).reshape(f0.shape)
        ax.contourf(f0, f1, pred, levels=1, colors=[color0, color1], alpha=0.25)
        ax.contour(f0, f1, pred, levels=[0.5])

        ax.set_xlim(xmin, xmax)
        ax.set_ylim(ymin, ymax)
        ax.tick_params(bottom=False, left=False, labelbottom=False, labelleft=False)
        ax.set_title("hidden_units=[{},{}]".format(units0, units1))
plt.show()

units0_list = [1, 5, 10]

units1_list = [1, 5, 10]

for row, units0 in enumerate(units0_list):

for col, units1 in enumerate(units1_list):

ax = axs[row, col]

ax.scatter(Xtr0[:, 0], Xtr0[:, 1], marker='o', s=20, color=color0)

ax.scatter(Xtr1[:, 0], Xtr1[:, 1], marker='^', s=20, color=color1)

mlp = MLPClassifier(solver='lbfgs', random_state=0,

hidden_layer_sizes=[units0, units1]).fit(X_train, y_train)

pred = mlp.predict(np.vstack([f0.ravel(), f1.ravel()]).T).reshape(f0.shape)

ax.contourf(f0, f1, pred, levels=1, colors=[color0, color1], alpha=0.25)

ax.contour(f0, f1, pred, levels=[0.5])

ax.set_xlim(xmin, xmax)

ax.set_ylim(ymin, ymax)

ax.tick_params(bottom=False, left=False, labelbottom=False, labelleft=False)

ax.set_title("hidden_units=[{},{}]".format(units0, units1))

plt.show()

活性化関数tanh

デフォルトでは非線形活性化関数にReLUが用いられるが、これをtanhとすることで下図のように決定境界が滑らかになる。デフォルトのまま（右）だと書籍のような形にならないが、最大計算回数max_iter=115と制限すると大体似たような形になる。

max_iter_list = [115, 200]
for max_iter, ax in zip(max_iter_list, axs_1d):
    ax.scatter(Xtr0[:, 0], Xtr0[:, 1], marker='o', s=80, color=color0)
    ax.scatter(Xtr1[:, 0], Xtr1[:, 1], marker='^', s=80, color=color1)

    mlp = MLPClassifier(solver='lbfgs', activation='tanh', random_state=0,
        hidden_layer_sizes=[10, 10], max_iter=max_iter).fit(X_train, y_train)
    pred = mlp.predict(np.vstack([f0.ravel(), f1.ravel()]).T).reshape(f0.shape)
    ax.contourf(f0, f1, pred, levels=1, colors=[color0, color1], alpha=0.25)
    ax.contour(f0, f1, pred, levels=[0.5])

    ax.set_xlim(xmin, xmax)
    ax.set_ylim(ymin, ymax)
    ax.tick_params(bottom=False, left=False, labelbottom=False, labelleft=False)
    ax.set_title("max_iter={}".format(max_iter))
plt.show()

max_iter_list = [115, 200]

for max_iter, ax in zip(max_iter_list, axs_1d):

ax.scatter(Xtr0[:, 0], Xtr0[:, 1], marker='o', s=80, color=color0)

ax.scatter(Xtr1[:, 0], Xtr1[:, 1], marker='^', s=80, color=color1)

mlp = MLPClassifier(solver='lbfgs', activation='tanh', random_state=0,

hidden_layer_sizes=[10, 10], max_iter=max_iter).fit(X_train, y_train)

pred = mlp.predict(np.vstack([f0.ravel(), f1.ravel()]).T).reshape(f0.shape)

ax.contourf(f0, f1, pred, levels=1, colors=[color0, color1], alpha=0.25)

ax.contour(f0, f1, pred, levels=[0.5])

ax.set_xlim(xmin, xmax)

ax.set_ylim(ymin, ymax)

ax.tick_params(bottom=False, left=False, labelbottom=False, labelleft=False)

ax.set_title("max_iter={}".format(max_iter))

plt.show()

ここでも2つの隠れ層のユニット数を変化させてみると、第1層が大まかな形、第2層が細部の表現に影響していると言えそうだ。

正則化

MLPClassifierはL2正則化が可能で、パラメーターalphaに大きな値を設定すると正則化を強くできる。デフォルトはalpha=0.0001で正則化が効いていない状態。

以下に、2層のユニット数[10, 10]と[100, 100]に対してalphaをデフォルトの0.0001から1.0まで変化させたときの様子を示す。ただしmax_iter=500として未収束の警告が出ないようにしている。alphaを大きくするにしたがって正則化が強くなり、決定境界がシンプルなものになっていく様子が見られる。

units = [10, 100]
alphas = [0.0001, 0.01, 0.1, 1]
for axr, unit in zip(axs, units):
    for ax, alpha in zip(axr, alphas):
        ax.scatter(Xtr0[:, 0], Xtr0[:, 1], marker='o', s=20, color=color0)
        ax.scatter(Xtr1[:, 0], Xtr1[:, 1], marker='^', s=20, color=color1)

        mlp = MLPClassifier(solver='lbfgs', random_state=0,
            hidden_layer_sizes=[unit, unit], alpha=alpha,
            max_iter=500).fit(X_train, y_train)
        pred = mlp.predict(np.vstack([f0.ravel(), f1.ravel()]).T).reshape(f0.shape)
        ax.contourf(f0, f1, pred, levels=1, colors=[color0, color1], alpha=0.25)
        ax.contour(f0, f1, pred, levels=[0.5])

        ax.set_title("units={}, alpha={}".format(unit, alpha), fontsize=8)
        ax.set_xlim(xmin, xmax)
        ax.set_ylim(ymin, ymax)
        ax.tick_params(bottom=False, left=False, labelbottom=False, labelleft=False)
plt.show()

units = [10, 100]

alphas = [0.0001, 0.01, 0.1, 1]

for axr, unit in zip(axs, units):

for ax, alpha in zip(axr, alphas):

ax.scatter(Xtr0[:, 0], Xtr0[:, 1], marker='o', s=20, color=color0)

ax.scatter(Xtr1[:, 0], Xtr1[:, 1], marker='^', s=20, color=color1)

mlp = MLPClassifier(solver='lbfgs', random_state=0,

hidden_layer_sizes=[unit, unit], alpha=alpha,

max_iter=500).fit(X_train, y_train)

pred = mlp.predict(np.vstack([f0.ravel(), f1.ravel()]).T).reshape(f0.shape)

ax.contourf(f0, f1, pred, levels=1, colors=[color0, color1], alpha=0.25)

ax.contour(f0, f1, pred, levels=[0.5])

ax.set_title("units={}, alpha={}".format(unit, alpha), fontsize=8)

ax.set_xlim(xmin, xmax)

ax.set_ylim(ymin, ymax)

ax.tick_params(bottom=False, left=False, labelbottom=False, labelleft=False)

plt.show()

ランダムな重みづけの影響

ニューラルネットワークでは、学習開始前に各重み係数がランダムに割り当てられるため、その初期値がモデルに影響を与える。以下は同じパラメーター設定に対してrandom_stateのみを変化させたもので、決定境界の形が異なっている。

データの前処理等

MLPのBreast cancerデータセットへの適用例で、データの標準化や重み係数の分布の確認等を行っている。

今後の課題

総数・ユニット数と計算量の関係
パラメーター調整のパターン
scikit-learn以外のライブラリー(keras, lasagna, tensor-flow)
GPUのサポート
収束計算のアルゴリズム(lbfgs, adam, sgd)

Breast cancerデータセット – MLP

2020-07-04 / tau / コメントする

精度不足

書籍”Pythonではじめる機械学習”の”2.3.8.2 ニューラルネットワークのチューニング”で、scikit-learnのMLPをBreast Cancerデータセットに適用した例が示されている。

デフォルトのパラメーターのままで実行した例は以下の通りだが、訓練スコアとテストスコアは、書籍ではそれぞれ0.92と0.90となっていて、下の結果とは異なる。

from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
from sklearn.neural_network import MLPClassifier

ds = load_breast_cancer()
X_train, X_test, y_train, y_test = \
    train_test_split(ds.data, ds.target, random_state=0)

print("for raw data")
mlp = MLPClassifier(random_state=42).fit(X_train, y_train)
print("Training score: {:.3f}".format(mlp.score(X_train, y_train)))
print("Test score    : {:.3f}".format(mlp.score(X_test, y_test)))

# for raw data
# Training score: 0.939
# Test score    : 0.916

from sklearn.datasets import load_breast_cancer

from sklearn.model_selection import train_test_split

from sklearn.neural_network import MLPClassifier

ds = load_breast_cancer()

X_train, X_test, y_train, y_test = \

train_test_split(ds.data, ds.target, random_state=0)

print("for raw data")

mlp = MLPClassifier(random_state=42).fit(X_train, y_train)

print("Training score: {:.3f}".format(mlp.score(X_train, y_train)))

print("Test score : {:.3f}".format(mlp.score(X_test, y_test)))

# for raw data

# Training score: 0.939

# Test score : 0.916

データの標準化

これに対して書籍では、特徴量データを標準化(standardize)する例を示している。同じコードで計算したのが以下の結果で、この場合は書籍と同じ値となっている。

mean_train = X_train.mean(axis=0)
std_train = X_train.std(axis=0)
X_train_scaled = (X_train - mean_train) / std_train
X_test_scaled = (X_test - mean_train) / std_train

print("for scaled data")
mlp = MLPClassifier(random_state=0).fit(X_train_scaled, y_train)
print("Training score: {:.3f}".format(mlp.score(X_train_scaled, y_train)))
print("Test score    : {:.3f}".format(mlp.score(X_test_scaled, y_test)))

# for scaled data
# Training score: 0.991
# Test score    : 0.965

mean_train = X_train.mean(axis=0)

std_train = X_train.std(axis=0)

X_train_scaled = (X_train - mean_train) / std_train

X_test_scaled = (X_test - mean_train) / std_train

print("for scaled data")

mlp = MLPClassifier(random_state=0).fit(X_train_scaled, y_train)

print("Training score: {:.3f}".format(mlp.score(X_train_scaled, y_train)))

print("Test score : {:.3f}".format(mlp.score(X_test_scaled, y_test)))

# for scaled data

# Training score: 0.991

# Test score : 0.965

ここで未収束の警告が出て、これも書籍と同じ。

ConvergenceWarning: Stochastic Optimizer: Maximum iterations (200) reached and the optimization hasn't converged yet.
  % self.max_iter, ConvergenceWarning)

1 2	ConvergenceWarning: Stochastic Optimizer: Maximum iterations (200) reached and the optimization hasn't converged yet. % self.max_iter, ConvergenceWarning)

書籍に倣ってmax_iter=1000とすると正常終了するが、今度は書籍の結果(0.995/0.965)と異なる結果となってしまう。

mlp = MLPClassifier(max_iter=1000, random_state=0).fit(X_train_scaled, y_train)
print("Training score: {:.3f}".format(mlp.score(X_train_scaled, y_train)))
print("Test score    : {:.3f}".format(mlp.score(X_test_scaled, y_test)))

# Training score: 1.000
# Test score    : 0.972

mlp = MLPClassifier(max_iter=1000, random_state=0).fit(X_train_scaled, y_train)

print("Training score: {:.3f}".format(mlp.score(X_train_scaled, y_train)))

print("Test score : {:.3f}".format(mlp.score(X_test_scaled, y_test)))

# Training score: 1.000

# Test score : 0.972

random_stateが違う？

よく見ると、最初のコードではMPLClassifierのパラメーターでrandom_state=42とそれ以前と同じ値を使っているが、その後の2つの計算ではrandom_state=0と異なる値を使っている。MLPの解説で重みの初期値に影響するrandom_stateの値によってモデルが異なることを注意しているにもかかわらず、このパラメーターを変更している理由がよくわからない（値を42に揃えてみたところ、ドラスティックな変化はなかったが）。

重み係数の分布

最後に、書籍に掲載されているimshowを使った重み係数の分布を再現してみる。imshowは画像ファイルを表示するほかに、配列を与えてその内容に応じたイメージを表示できる。colorbarは扱いがややこしそうで、Axesに対して適当なメソッドが見当たらなかったので、ここではpyplotに直接描画している。

import matplotlib.pyplot as plt
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
from sklearn.neural_network import MLPClassifier

ds = load_breast_cancer()
X_train, X_test, y_train, y_test = \
    train_test_split(ds.data, ds.target, random_state=0)

mlp = MLPClassifier(random_state=42, hidden_layer_sizes=[100]).fit(X_train, y_train)

plt.figure(figsize=(20, 5))
plt.imshow(mlp.coefs_[0], interpolation='none', cmap='viridis')
plt.yticks(range(30), ds.feature_names)
plt.xlabel("weights for features in hidden layer")
plt.ylabel("Feature names")
plt.colorbar()
plt.show()

import matplotlib.pyplot as plt

from sklearn.datasets import load_breast_cancer

from sklearn.model_selection import train_test_split

from sklearn.neural_network import MLPClassifier

ds = load_breast_cancer()

X_train, X_test, y_train, y_test = \

train_test_split(ds.data, ds.target, random_state=0)

mlp = MLPClassifier(random_state=42, hidden_layer_sizes=[100]).fit(X_train, y_train)

plt.figure(figsize=(20, 5))

plt.imshow(mlp.coefs_[0], interpolation='none', cmap='viridis')

plt.yticks(range(30), ds.feature_names)

plt.xlabel("weights for features in hidden layer")

plt.ylabel("Feature names")

plt.colorbar()

plt.show()

Python/pyplot – 決定境界の描き方

2020-07-02 / tau / コメントする

決定境界の描き方として以前ループを使った泥臭い方法を考えたが、meshgridを使って数行で書けることを知ったのでまとめ。

結論としては以下の19～25行目の8行で、以下の手順で決定境界を書いている。

2つの特徴量の全領域をカバーする値をnumpy.linspace()で生成
numpy.meshgrid()で2次元のグリッドに変換
各特徴量のメッシュグリッドを1次元に変形し、縦2列の配列化
prediction()メソッドでその配列の各座標に対応する予測値を計算（結果は1次元配列）
結果の配列をmeshgridと同じ形状の2次元配列に変形
contour/contourf()で決定境界を描画

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_moons
from sklearn.neighbors import KNeighborsClassifier

X, y = make_moons(n_samples=100, noise=0.25, random_state=3)

x0_min, x0_max = -2.0, 2.5
x1_min, x1_max = -1.0, 1.5

knn = KNeighborsClassifier(n_neighbors=3).fit(X, y)

fig, ax = plt.subplots()

color0, color1 = 'tab:blue', 'tab:orange'
ax.scatter(X[y==0][:, 0], X[y==0][:, 1], marker='o')
ax.scatter(X[y==1][:, 0], X[y==1][:, 1], marker='^')

f0 = np.linspace(x0_min, x0_max, 200)
f1 = np.linspace(x1_min, x1_max, 200)
f0, f1 = np.meshgrid(f0, f1)
pred = knn.predict(np.hstack([f0.reshape(-1, 1), f1.reshape(-1, 1)])) \
        .reshape(f0.shape)
ax.contour(f0, f1, pred, levels=[0.5])
ax.contourf(f0, f1, pred, levels=1, colors=[color0, color1], alpha=0.25)

ax.set_xlim(x0_min, x0_max)
ax.set_ylim(x1_min, x1_max)
ax.set_xlabel("Feature-0")
ax.set_ylabel("Feature-1")

plt.show()

import numpy as np

import matplotlib.pyplot as plt

from sklearn.datasets import make_moons

from sklearn.neighbors import KNeighborsClassifier

X, y = make_moons(n_samples=100, noise=0.25, random_state=3)

x0_min, x0_max = -2.0, 2.5

x1_min, x1_max = -1.0, 1.5

knn = KNeighborsClassifier(n_neighbors=3).fit(X, y)

fig, ax = plt.subplots()

color0, color1 = 'tab:blue', 'tab:orange'

ax.scatter(X[y==0][:, 0], X[y==0][:, 1], marker='o')

ax.scatter(X[y==1][:, 0], X[y==1][:, 1], marker='^')

f0 = np.linspace(x0_min, x0_max, 200)

f1 = np.linspace(x1_min, x1_max, 200)

f0, f1 = np.meshgrid(f0, f1)

pred = knn.predict(np.hstack([f0.reshape(-1, 1), f1.reshape(-1, 1)])) \

.reshape(f0.shape)

ax.contour(f0, f1, pred, levels=[0.5])

ax.contourf(f0, f1, pred, levels=1, colors=[color0, color1], alpha=0.25)

ax.set_xlim(x0_min, x0_max)

ax.set_ylim(x1_min, x1_max)

ax.set_xlabel("Feature-0")

ax.set_ylabel("Feature-1")

plt.show()

具体的な変数の変形状況を要素数4の少ない例で示すと以下の通り。

まず、2つの特徴量の範囲の数列を生成する。

f0 = np.linspace(x0_min, x0_max, 4)
f1 = np.linspace(x1_min, x1_max, 4)
print(f0)
print(f1)

# [-2.  -0.5  1.   2.5]
# [-1.         -0.16666667  0.66666667  1.5       ]

f0 = np.linspace(x0_min, x0_max, 4)

f1 = np.linspace(x1_min, x1_max, 4)

print(f0)

print(f1)

# [-2. -0.5 1. 2.5]

# [-1. -0.16666667 0.66666667 1.5 ]

それらの数列を、meshgridで2次元配列に変形する。

f0, f1 = np.meshgrid(f0, f1)
print(f0)
print(f1)

# [[-2.  -0.5  1.   2.5]
#  [-2.  -0.5  1.   2.5]
#  [-2.  -0.5  1.   2.5]
#  [-2.  -0.5  1.   2.5]]
# [[-1.         -1.         -1.         -1.        ]
#  [-0.16666667 -0.16666667 -0.16666667 -0.16666667]
#  [ 0.66666667  0.66666667  0.66666667  0.66666667]
#  [ 1.5         1.5         1.5         1.5       ]]

f0, f1 = np.meshgrid(f0, f1)

print(f0)

print(f1)

# [[-2. -0.5 1. 2.5]

# [-2. -0.5 1. 2.5]

# [-2. -0.5 1. 2.5]]

# [[-1. -1. -1. -1. ]

# [-0.16666667 -0.16666667 -0.16666667 -0.16666667]

# [ 0.66666667 0.66666667 0.66666667 0.66666667]

# [ 1.5 1.5 1.5 1.5 ]]

予測モデルに与える変数は各特徴量を列とする2次元配列とする必要があるので、まず上の2次元配列をそれぞれ1次元に変形。この変形では、2次元配列の各行を連ねていった1行の配列を列ベクトルにした形になる。

print(f0.reshape(-1, 1))
print(f1.reshape(-1, 1))

# [[-2. ]
#  [-0.5]
#  [ 1. ]
#  [ 2.5]
#  [-2. ]
#  [-0.5]
#  [ 1. ]
#  [ 2.5]
#  [-2. ]
#  [-0.5]
#  [ 1. ]
#  [ 2.5]
#  [-2. ]
#  [-0.5]
#  [ 1. ]
#  [ 2.5]]
# [[-1.        ]
#  [-1.        ]
#  [-1.        ]
#  [-1.        ]
#  [-0.16666667]
#  [-0.16666667]
#  [-0.16666667]
#  [-0.16666667]
#  [ 0.66666667]
#  [ 0.66666667]
#  [ 0.66666667]
#  [ 0.66666667]
#  [ 1.5       ]
#  [ 1.5       ]
#  [ 1.5       ]
#  [ 1.5       ]]

print(f0.reshape(-1, 1))

print(f1.reshape(-1, 1))

# [[-2. ]

# [-0.5]

# [ 1. ]

# [ 2.5]

# [-2. ]

# [-0.5]

# [ 1. ]

# [ 2.5]

# [-2. ]

# [-0.5]

# [ 1. ]

# [ 2.5]

# [-2. ]

# [-0.5]

# [ 1. ]

# [ 2.5]]

# [[-1. ]

# [-1. ]

# [-0.16666667]

# [ 0.66666667]

# [ 1.5 ]

# [ 1.5 ]]

次に2つの列ベクトルを横方向に並べて、総計算データ数×特徴量数(2)の2次元配列とする。

print(np.hstack([f0.reshape(-1, 1), f1.reshape(-1, 1)]))

# [[-2.         -1.        ]
#  [-0.5        -1.        ]
#  [ 1.         -1.        ]
#  [ 2.5        -1.        ]
#  [-2.         -0.16666667]
#  [-0.5        -0.16666667]
#  [ 1.         -0.16666667]
#  [ 2.5        -0.16666667]
#  [-2.          0.66666667]
#  [-0.5         0.66666667]
#  [ 1.          0.66666667]
#  [ 2.5         0.66666667]
#  [-2.          1.5       ]
#  [-0.5         1.5       ]
#  [ 1.          1.5       ]
#  [ 2.5         1.5       ]]

print(np.hstack([f0.reshape(-1, 1), f1.reshape(-1, 1)]))

# [[-2. -1. ]

# [-0.5 -1. ]

# [ 1. -1. ]

# [ 2.5 -1. ]

# [-2. -0.16666667]

# [-0.5 -0.16666667]

# [ 1. -0.16666667]

# [ 2.5 -0.16666667]

# [-2. 0.66666667]

# [-0.5 0.66666667]

# [ 1. 0.66666667]

# [ 2.5 0.66666667]

# [-2. 1.5 ]

# [-0.5 1.5 ]

# [ 1. 1.5 ]

# [ 2.5 1.5 ]]

この配列の各座標に対する予測値を、predict()メソッドで予測。この結果は、1次元化されたf0やf1と同じく、2次元のmeshgridの各行を横に連ねたものになっている。

print(knn.predict(np.hstack([f0.reshape(-1, 1), f1.reshape(-1, 1)])))

# [0 0 1 1 0 1 1 1 0 0 0 1 0 0 0 1]

print(knn.predict(np.hstack([f0.reshape(-1, 1), f1.reshape(-1, 1)])))

# [0 0 1 1 0 1 1 1 0 0 0 1 0 0 0 1]

この結果を、meshgrid化されたf0（またはf1）と同じ形に変形。これで予測結果がf0×f1平面の各座標に対応した予測値の2次元配列となっている。

print(knn.predict(np.hstack([f0.reshape(-1, 1), f1.reshape(-1, 1)])).reshape(f0.shape))

# [[0 0 1 1]
#  [0 1 1 1]
#  [0 0 0 1]
#  [0 0 0 1]]

print(knn.predict(np.hstack([f0.reshape(-1, 1), f1.reshape(-1, 1)])).reshape(f0.shape))

# [[0 0 1 1]

# [0 1 1 1]

# [0 0 0 1]

# [0 0 0 1]]

この結果を使い、contour()/contourf()で決定境界あるいは決定領域を描画。

pred = knn.predict(np.hstack([f0.reshape(-1, 1), f1.reshape(-1, 1)])) \
        .reshape(f0.shape)
ax.contour(f0, f1, pred, levels=[0.5])
ax.contourf(f0, f1, pred, levels=1, colors=[color0, color1], alpha=0.25)

pred = knn.predict(np.hstack([f0.reshape(-1, 1), f1.reshape(-1, 1)])) \

.reshape(f0.shape)

ax.contour(f0, f1, pred, levels=[0.5])

ax.contourf(f0, f1, pred, levels=1, colors=[color0, color1], alpha=0.25)

ここでlevelsの指定は以下のようにしている。

まずcontour()の場合、ドキュメンテーションには“If an int n, use n data intervals; i.e. draw n+1 contour lines. The level heights are automatically chosen.”と書かれているので、levels=0と指定すると0＋1本の線が描かれると考えたが以下のような警告が出て線の位置がずれた。

serWarning: No contour levels were found within the data range.
  ax.contour(f0, f1, pred, levels=0)

1 2	serWarning: No contour levels were found within the data range. ax.contour(f0, f1, pred, levels=0)

そこでlevels=[0.5]と2つのクラス値0と1の間をとると適切に表示される。

なおcontourf()のときは、levels=1として2つの領域が描かれる。

Breast Cancerデータセット – SVM

2020-06-29 / tau / コメントする

過学習？

書籍”Pythonではじめる機械学習”の”2.3.7.4 SVMパラメータの調整”の最後の方で、scikit-learnのSVMをBreast Cancerデータセットに適用した例が示されている（カーネル法によるSVMについてはこちらにまとめている）。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
from sklearn.svm import SVC

ds = load_breast_cancer()
X, y = ds.data, ds.target

X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)

svc = SVC(gamma='auto').fit(X_train, y_train)

print("Training score: {:.3f}".format(svc.score(X_train, y_train)))
print("Test score    : {:.3f}".format(svc.score(X_test, y_test)))

# Training score: 1.000
# Test score    : 0.629

import numpy as np

import matplotlib.pyplot as plt

from sklearn.datasets import load_breast_cancer

from sklearn.model_selection import train_test_split

from sklearn.svm import SVC

ds = load_breast_cancer()

X, y = ds.data, ds.target

X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)

svc = SVC(gamma='auto').fit(X_train, y_train)

print("Training score: {:.3f}".format(svc.score(X_train, y_train)))

print("Test score : {:.3f}".format(svc.score(X_test, y_test)))

# Training score: 1.000

# Test score : 0.629

ここで、原典ではSVC()の引数を指定せずデフォルトのままとしているが、そのまま実行すると以下のような結果になった。

Training score: 0.904
Test score    : 0.937

1 2	Training score: 0.904 Test score : 0.937

scikit-learnのドキュメンテーションによると、

Kernel coefficient for ‘rbf’, ‘poly’ and ‘sigmoid’.

if gamma='scale' (default) is passed then it uses 1 / (n_features * X.var()) as value of gamma,
if ‘auto’, uses 1 / n_features.

Changed in version 0.22: The default value of gamma changed from ‘auto’ to ‘scale’.

とされていて、gammaのデフォルト設定が変わったようである。新しい仕様ではデフォルトでデータのスケーリングが行われるため、どちらかといえば適合不足の状態になる。先のコードでは明示的にgamma=autoを設定し、書籍と同じ結果を得ている。

特徴量データのサイズの違い

Breast Cancerデータの30の特徴量について、各々の分布状況を箱髭図で描いてみた。縦軸の対数スケールに対してでも、各特徴量がかなりばらついており、1万倍～100万倍ほどの違いがあることがわかる。

import matplotlib.pyplot as plt
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split

ds = load_breast_cancer()
X, y = ds.data, ds.target

X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)

fig, ax = plt.subplots(figsize=(6.4, 6))
fig.subplots_adjust(bottom=0.3)

ax.boxplot(X_train, showfliers=False)
ax.set_xticklabels(ds.feature_names, rotation=270, fontsize=8)
ax.set_yscale('log')

plt.show()

import matplotlib.pyplot as plt

from sklearn.datasets import load_breast_cancer

from sklearn.model_selection import train_test_split

ds = load_breast_cancer()

X, y = ds.data, ds.target

X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)

fig, ax = plt.subplots(figsize=(6.4, 6))

fig.subplots_adjust(bottom=0.3)

ax.boxplot(X_train, showfliers=False)

ax.set_xticklabels(ds.feature_names, rotation=270, fontsize=8)

ax.set_yscale('log')

plt.show()

データの前処理

データのスケールを揃えるために使われるMiniMaxScalorでは、各特徴量の訓練データを最小値と最大値でスケーリングし、0～1に納まるようにする。具体的には、特徴量ごとに最小値を引いて、最大値－最小値のレンジで除する。

from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
from sklearn.svm import SVC

ds = load_breast_cancer()
X, y = ds.data, ds.target

X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)

min_features = X_train.min(axis=0)
max_features = X_train.max(axis=0)
ranges = max_features - min_features

X_train_scaled = (X_train - min_features) / ranges
print("Scaled training data:")
print("Minimum for each feature\n{}".format(X_train_scaled.min(axis=0)))
print("Maximum for each feature\n{}".format(X_train_scaled.max(axis=0)))
print()
X_test_scaled = (X_test - min_features) / ranges
print("Scaled test data:")
print("Minimum for each feature\n{}".format(X_test_scaled.min(axis=0)))
print("Maximum for each feature\n{}".format(X_test_scaled.max(axis=0)))

from sklearn.datasets import load_breast_cancer

from sklearn.model_selection import train_test_split

from sklearn.svm import SVC

ds = load_breast_cancer()

X, y = ds.data, ds.target

X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)

min_features = X_train.min(axis=0)

max_features = X_train.max(axis=0)

ranges = max_features - min_features

X_train_scaled = (X_train - min_features) / ranges

print("Scaled training data:")

print("Minimum for each feature\n{}".format(X_train_scaled.min(axis=0)))

print("Maximum for each feature\n{}".format(X_train_scaled.max(axis=0)))

print()

X_test_scaled = (X_test - min_features) / ranges

print("Scaled test data:")

print("Minimum for each feature\n{}".format(X_test_scaled.min(axis=0)))

print("Maximum for each feature\n{}".format(X_test_scaled.max(axis=0)))

この結果、訓練データの各特徴量の最小値はすべて0となり、最大値はすべて1となる。

Scaled training data:
Minimum for each feature
[0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
 0. 0. 0. 0. 0. 0.]
Maximum for each feature
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
 1. 1. 1. 1. 1. 1.]

Scaled training data:

Minimum for each feature

[0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.

0. 0. 0. 0. 0. 0.]

Maximum for each feature

[1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.

1. 1. 1. 1. 1. 1.]

テストデータに対してもスケーリングを行うが、ここで使う最小値とレンジは訓練データのものとし、訓練データとテストデータでスケーリングに歪がでないようにする。その結果、スケーリング後のテストデータには、最小値が0より小さい値や最大値が1より大きい値が出ている。

Scaled test data:
Minimum for each feature
[ 0.03540158  0.04190871  0.02895446  0.01497349  0.14260888  0.04999658
  0.          0.          0.07222222  0.00589722  0.00105015 -0.00057494
  0.00067851 -0.0007963   0.05148726  0.01434497  0.          0.
  0.04195752  0.01113138  0.03678406  0.01252665  0.03366702  0.01400904
  0.08531995  0.01833687  0.          0.          0.00749064  0.02367834]
Maximum for each feature
[0.76809125 1.22697095 0.75813696 0.64750795 1.20310633 1.11643038
 0.99906279 0.90606362 0.93232323 0.94903117 0.45573058 0.72623944
 0.48593507 0.31641282 1.36082713 1.2784499  0.36313131 0.77476795
 1.32643996 0.72672498 0.82106012 0.87553305 0.77887345 0.67803775
 0.78603975 0.87843331 0.93450479 1.0024113  0.76384782 0.58743277]

Scaled test data:

Minimum for each feature

[ 0.03540158 0.04190871 0.02895446 0.01497349 0.14260888 0.04999658

0. 0. 0.07222222 0.00589722 0.00105015 -0.00057494

0.00067851 -0.0007963 0.05148726 0.01434497 0. 0.

0.04195752 0.01113138 0.03678406 0.01252665 0.03366702 0.01400904

0.08531995 0.01833687 0. 0. 0.00749064 0.02367834]

Maximum for each feature

[0.76809125 1.22697095 0.75813696 0.64750795 1.20310633 1.11643038

0.99906279 0.90606362 0.93232323 0.94903117 0.45573058 0.72623944

0.48593507 0.31641282 1.36082713 1.2784499 0.36313131 0.77476795

1.32643996 0.72672498 0.82106012 0.87553305 0.77887345 0.67803775

0.78603975 0.87843331 0.93450479 1.0024113 0.76384782 0.58743277]

スケーリングされた訓練データとテストデータについてスコアを計算すると以下のようになり、先ほどの過学習の状態から適合不足の状態となった。尚この結果は、新しいSVCクラスにおいてデフォルトのgamma='auto'を指定したときの傾向と似ていて、若干の適合不足となっている。

svc = SVC(gamma='auto').fit(X_train_scaled, y_train)

print("Training score:{:.3f}".format(svc.score(X_train_scaled, y_train)))
print("Test score    :{:.3f}".format(svc.score(X_test_scaled, y_test)))

# Training score:0.948
# Test score    :0.951

svc = SVC(gamma='auto').fit(X_train_scaled, y_train)

print("Training score:{:.3f}".format(svc.score(X_train_scaled, y_train)))

print("Test score :{:.3f}".format(svc.score(X_test_scaled, y_test)))

# Training score:0.948

# Test score :0.951

パラメーター調整

上記の適合不足の結果に対して、パラメーターを変化させてみる。デフォルトのC=1からC=1000としてみると、訓練スコア、テストスコアとも改善された。テストスコアはランダムフォレストや決定木の勾配ブースティングの結果と同じになっている。

svc = SVC(C=1000, gamma='auto').fit(X_train_scaled, y_train)

print("Training score:{:.3f}".format(svc.score(X_train_scaled, y_train)))
print("Test score    :{:.3f}".format(svc.score(X_test_scaled, y_test)))

# Training score:0.988
# Test score    :0.972

svc = SVC(C=1000, gamma='auto').fit(X_train_scaled, y_train)

print("Training score:{:.3f}".format(svc.score(X_train_scaled, y_train)))

print("Test score :{:.3f}".format(svc.score(X_test_scaled, y_test)))

# Training score:0.988

# Test score :0.972

さらにいくつかのCとgammaで試してみると、特にスコアがいいのは以下のケースだった。なおgamma=1, 10の場合、C=100, 1000, 10000に対して訓練スコアが1.000、テストスコアが0.95程度で全て過学習となった。

C	gamma	訓練スコア	テストスコア
1000	auto	0.988	0.972
1000	0.01	0.986	0.979
100	0.1	0.986	0.972

SVM～カーネル法

2020-06-24 / tau / コメントする

概要

書籍”Pythonではじめる機械学習”の2.3.7 カーネル法を用いた”サポートベクタマシン”の写経

線形特徴量の非線形化

線形モデルでは分離不可能なデータ

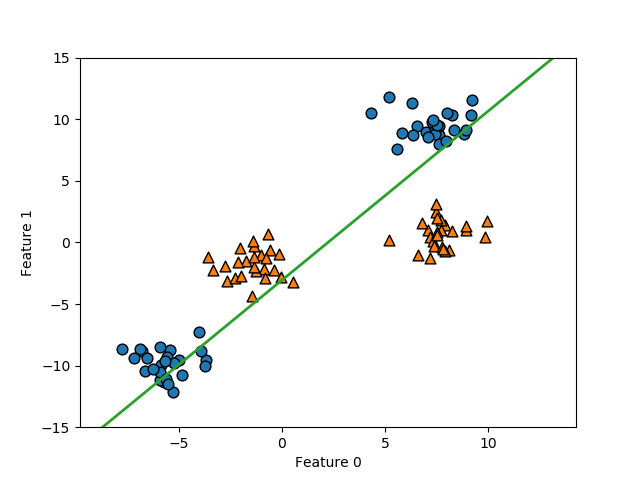
以下は、scikit-learnのmake_blobs()により生成した2特徴量、2クラス分類のデータに線形サポートベクターマシンを適用した例。このとき、決定境界は以下のように得られる。

(1) $\begin{gather*} b + w_0 f_0 + w_1 f_1 = 0\\ b \approx -0.2817,\; w_0 \approx 0.1261,\; w_1 \approx -0.0918 \end{gather*}$

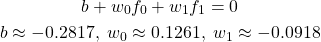
決定境界より上側では多項式の値は負となり、下側では正となるが、この境界は明らかに2つのクラスを分割していない。このように単純な例でも、線形モデルでは的確なクラス分類はできない。

以下のコードでは、原典と以下が異なっている。

収束しないという警告を受けて、LinearSVCのmax_iterをデフォルトの1000より大きな値としている

import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
from sklearn.svm import LinearSVC

X, y = make_blobs(centers=4, random_state=8)
y = y % 2

linsvm = LinearSVC(max_iter=5500).fit(X, y)

y_min, y_max = -15, 15
b = linsvm.intercept_
w0 = linsvm.coef_[0][0]
w1 = linsvm.coef_[0][1]
x_lower = -(b + w1 * y_min) / w0
x_upper = -(b + w1 * y_max) / w0

fig, ax = plt.subplots()
X0 = X[y==0]
X1 = X[y==1]
ax.scatter(X0[:, 0], X0[:, 1], marker='o', s=60, ec='k')
ax.scatter(X1[:, 0], X1[:, 1], marker='^', s=60, ec='k')
ax.plot([x_lower, x_upper], [y_min, y_max], linewidth=2, c='tab:green')
ax.set_ylim(y_min, y_max)
ax.set_xlabel("Feature-0")
ax.set_ylabel("Feature-1")
plt.show()

import matplotlib.pyplot as plt

from sklearn.datasets import make_blobs

from sklearn.svm import LinearSVC

X, y = make_blobs(centers=4, random_state=8)

y = y % 2

linsvm = LinearSVC(max_iter=5500).fit(X, y)

y_min, y_max = -15, 15

b = linsvm.intercept_

w0 = linsvm.coef_[0][0]

w1 = linsvm.coef_[0][1]

x_lower = -(b + w1 * y_min) / w0

x_upper = -(b + w1 * y_max) / w0

fig, ax = plt.subplots()

X0 = X[y==0]

X1 = X[y==1]

ax.scatter(X0[:, 0], X0[:, 1], marker='o', s=60, ec='k')

ax.scatter(X1[:, 0], X1[:, 1], marker='^', s=60, ec='k')

ax.plot([x_lower, x_upper], [y_min, y_max], linewidth=2, c='tab:green')

ax.set_ylim(y_min, y_max)

ax.set_xlabel("Feature-0")

ax.set_ylabel("Feature-1")

plt.show()

非線形特徴量の追加

ここで、特徴量1の2乗を新たな特徴量として加える。この場合、3つの特徴量に対して3次元空間内に各点が位置し、それぞれがクラス0/1に属している。新たな特徴量の追加によって、その軸の方向に各点が立ち上がり、真ん中の三角形の点群と両側の丸印の点群が平面でうまく分割できそうである。

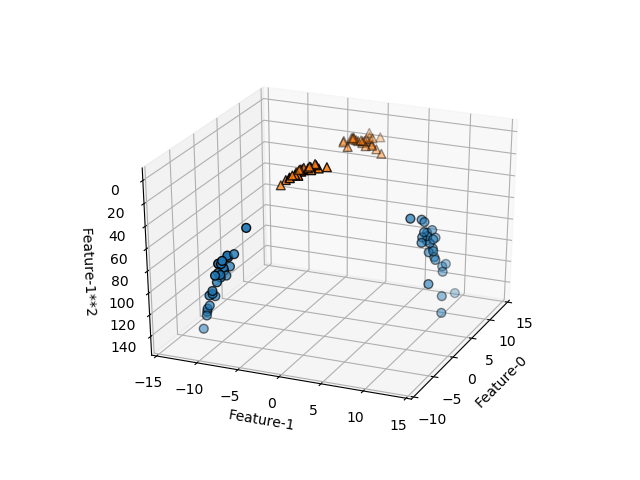
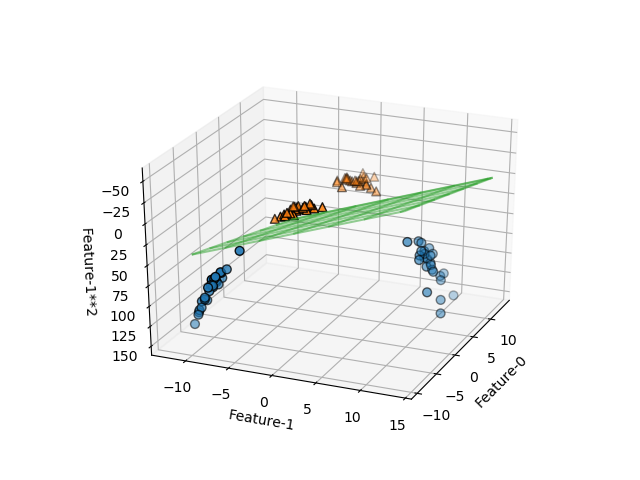
このデータセットに対して、線形SVMを適用し、決定境界を描いたのが以下の画像。特徴量が2つの場合の決定境界は直線だったが、特徴が3つになると決定境界は平面となる。予想通り、単純な平面で2つのクラスが分けられている。この決定境界の式は以下のようになる。

(2) $\begin{gather*} b + w_0 f_0 + w_1 f_1 + w_2 {f_1}^2 = 0\\ b \approx 1.1734,\; w_0 \approx 0.1301,\; w_1 \approx -0.2203,\; w_2 = -0.0597 \end{gather*}$

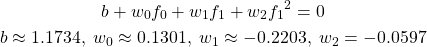
この平面に対して上側（f₁²が小さい側）では多項式の値は正となり、その反対側では負となる。

以下のコードは、原典と以下が異なっている。

収束しないという警告を受けて、LinearSVCのmax_iterをデフォルトの1000より大きな値としている
Axes3Dの生成の仕方を最新のバージョンに合ったものとしている
- 原典ではFigureオブジェクトを生成し、それをビューに関する引数とともにAxes3Dコンストラクターに渡している
- 本コードでは、subplotsの引数でprojectionを指定してFigureとAxes3Dを同時に生成し、veiw_init()でビューに関する引数を指定

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
from sklearn.svm import LinearSVC
from mpl_toolkits.mplot3d import Axes3D

X, y = make_blobs(centers=4, random_state=8)
y = y % 2
X_new = np.hstack((X, X[:, 1].reshape(-1, 1)**2))
X0, X1 = X_new[y==0], X_new[y==1]

linsvc = LinearSVC(max_iter=3700).fit(X_new, y)
intercept = linsvc.intercept_
coef = linsvc.coef_.ravel()

fig, ax = plt.subplots(subplot_kw=dict(projection='3d'))
ax.view_init(elev=-152, azim=-23)

u = np.linspace(X_new[:, 0].min() - 2, X_new[:, 1].max() + 2)
v = np.linspace(X_new[:, 0].min() - 2, X_new[:, 1].max() + 2)
u, v = np.meshgrid(u, v)
w = -(coef[0] * u + coef[1] * v + intercept) / coef[2]

ax.scatter(X0[:, 0], X0[:, 1], X0[:, 2], marker='o', s=40, ec='k')
ax.scatter(X1[:, 0], X1[:, 1], X1[:, 2], marker='^', s=40, ec='k')
ax.plot_wireframe(u, v, w, rstride=8, cstride=8, color='tab:green', alpha=0.5)

ax.set_xlabel("Feature-0")
ax.set_ylabel("Feature-1")
ax.set_zlabel("Feature-1**2")

plt.show()

import numpy as np

import matplotlib.pyplot as plt

from sklearn.datasets import make_blobs

from sklearn.svm import LinearSVC

from mpl_toolkits.mplot3d import Axes3D

X, y = make_blobs(centers=4, random_state=8)

y = y % 2

X_new = np.hstack((X, X[:, 1].reshape(-1, 1)**2))

X0, X1 = X_new[y==0], X_new[y==1]

linsvc = LinearSVC(max_iter=3700).fit(X_new, y)

intercept = linsvc.intercept_

coef = linsvc.coef_.ravel()

fig, ax = plt.subplots(subplot_kw=dict(projection='3d'))

ax.view_init(elev=-152, azim=-23)

u = np.linspace(X_new[:, 0].min() - 2, X_new[:, 1].max() + 2)

v = np.linspace(X_new[:, 0].min() - 2, X_new[:, 1].max() + 2)

u, v = np.meshgrid(u, v)

w = -(coef[0] * u + coef[1] * v + intercept) / coef[2]

ax.scatter(X0[:, 0], X0[:, 1], X0[:, 2], marker='o', s=40, ec='k')

ax.scatter(X1[:, 0], X1[:, 1], X1[:, 2], marker='^', s=40, ec='k')

ax.plot_wireframe(u, v, w, rstride=8, cstride=8, color='tab:green', alpha=0.5)

ax.set_xlabel("Feature-0")

ax.set_ylabel("Feature-1")

ax.set_zlabel("Feature-1**2")

plt.show()

元の特徴量に対する決定境界

上の例では特徴量は3つだが、最後の特徴量は2つ目の特徴量f₁から計算される量であり、実質は2つの特徴量が決まれば決定境界が決まる。3次元空間内の平面の決定境界を以下のように書きなおすと、このことが確認できる。

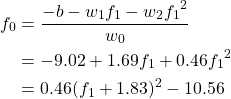
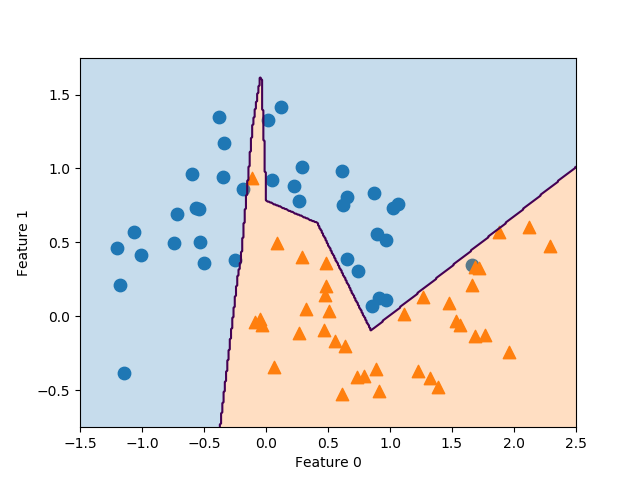
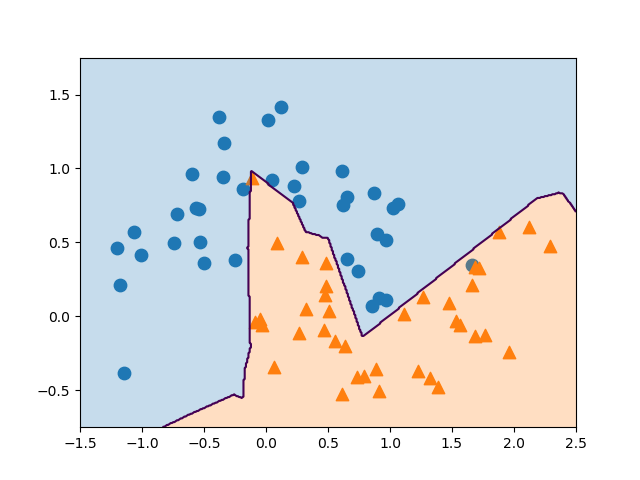
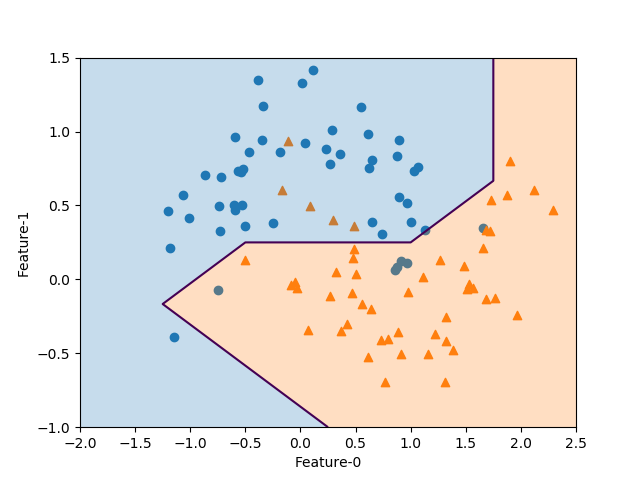
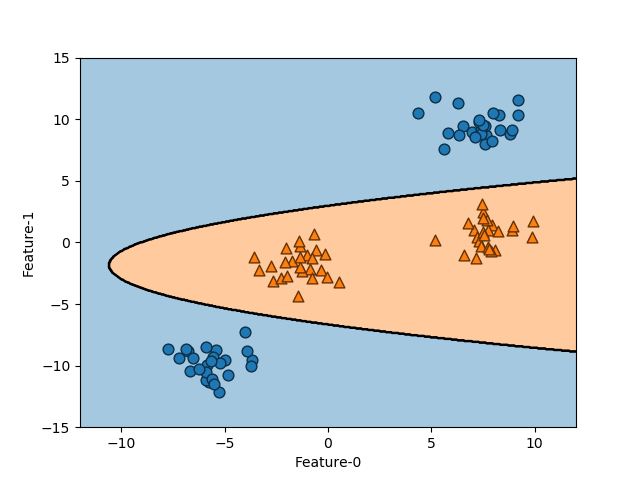
(3) $\begin{align*} f_0 &= \frac{-b - w_1 f_1 - w_2 {f_1}^2}{w_0} \\ &= -9.02 +1.69 f_1 + 0.46 {f_1}^2 \\ &= 0.46(f_1 +1.83)^2 - 10.56 \end{align*}$

これを2つの特徴量に対する決定境界として描画したのが以下の図で、境界が2次関数となっているのが確認できる。

SVMそのものは線形の決定境界しか得られないが、非線形化した特徴量を追加することによって、より複雑な決定境界とすることができる。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
from sklearn.svm import LinearSVC
from mpl_toolkits.mplot3d import Axes3D

X, y = make_blobs(centers=4, random_state=8)
y = y % 2
X_new = np.hstack((X, X[:, 1].reshape(-1, 1)**2))

linsvc = LinearSVC(max_iter=3700).fit(X_new, y)
intercept = linsvc.intercept_

x_min, x_max = -12, 12
y_min, y_max = -15, 15
u = np.linspace(x_min, x_max, 500)
v = np.linspace(y_min, y_max, 500)
u, v = np.meshgrid(u, v)
w = v**2
decision = linsvc.predict(np.c_[u.ravel(), v.ravel(), w.ravel()])

fig, ax = plt.subplots()

ax.scatter(X_new[y==0, 0], X_new[y==0, 1], marker='o', s=60, ec='k')
ax.scatter(X_new[y==1, 0], X_new[y==1, 1], marker='^', s=60, ec='k')
ax.contourf(u, v, decision.reshape(u.shape),
    levels=1, colors=['tab:blue', 'tab:orange'], alpha=0.4)
ax.contour(u, v, decision.reshape(u.shape), levels=1, colors='k')

ax.set_xlim(x_min, x_max)
ax.set_ylim(y_min, y_max)
ax.set_xlabel("Feature-0")
ax.set_ylabel("Feature-1")

plt.show()

import numpy as np

import matplotlib.pyplot as plt

from sklearn.datasets import make_blobs

from sklearn.svm import LinearSVC

from mpl_toolkits.mplot3d import Axes3D

X, y = make_blobs(centers=4, random_state=8)

y = y % 2

X_new = np.hstack((X, X[:, 1].reshape(-1, 1)**2))

linsvc = LinearSVC(max_iter=3700).fit(X_new, y)

intercept = linsvc.intercept_

x_min, x_max = -12, 12

y_min, y_max = -15, 15

u = np.linspace(x_min, x_max, 500)

v = np.linspace(y_min, y_max, 500)

u, v = np.meshgrid(u, v)

w = v**2

decision = linsvc.predict(np.c_[u.ravel(), v.ravel(), w.ravel()])

fig, ax = plt.subplots()

ax.scatter(X_new[y==0, 0], X_new[y==0, 1], marker='o', s=60, ec='k')

ax.scatter(X_new[y==1, 0], X_new[y==1, 1], marker='^', s=60, ec='k')

ax.contourf(u, v, decision.reshape(u.shape),

levels=1, colors=['tab:blue', 'tab:orange'], alpha=0.4)

ax.contour(u, v, decision.reshape(u.shape), levels=1, colors='k')

ax.set_xlim(x_min, x_max)

ax.set_ylim(y_min, y_max)

ax.set_xlabel("Feature-0")

ax.set_ylabel("Feature-1")

plt.show()

カーネルトリック

概要

上記の例では特徴量の1つを2次として新たな特徴量とした。特徴量の非線形化としては、このように特徴量の累乗とするほか、異なる特徴量同士の積を交互作用として導入することが考えられる。ただし、特徴量の数が多くなった時に、それらの全ての組み合わせに対する積を考えると、計算量が膨れ上がる。カーネルトリック(kernel trick)とは、拡張された特徴量空間でのデータ間の距離を、実際の拡張計算をせずに行う方法らしい。

受け売りをそのまま書いておくと、SVMで広く用いられているカーネルトリックのマッピング方法は以下の2つとのこと。

多項式カーネル(polynomial kernel)：もとの特徴量の特定の次数までの全ての多項式を計算
放射既定関数(radial basis function: RBF)カーネルとも呼ばれるガウシアンカーネル：直感的には全次数の全ての多項式を考えるが、次数が高くなるにつれて特徴量の重要性を小さくする

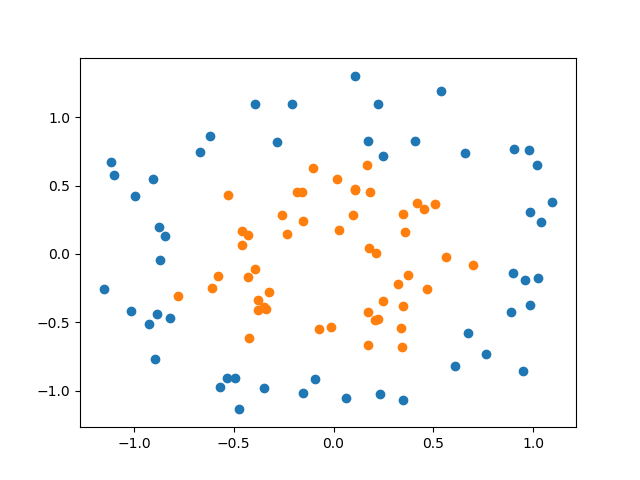
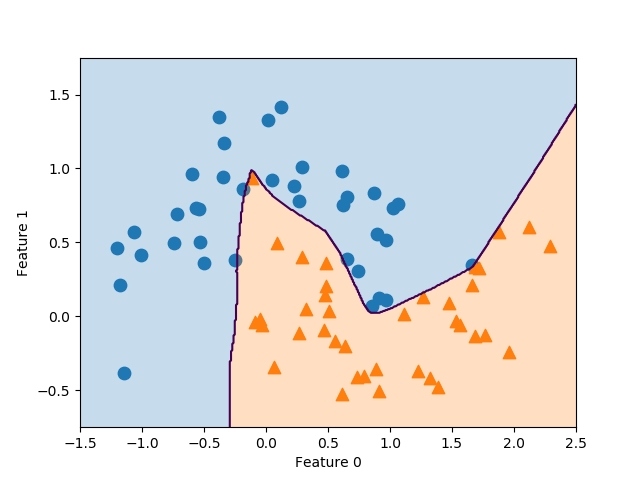
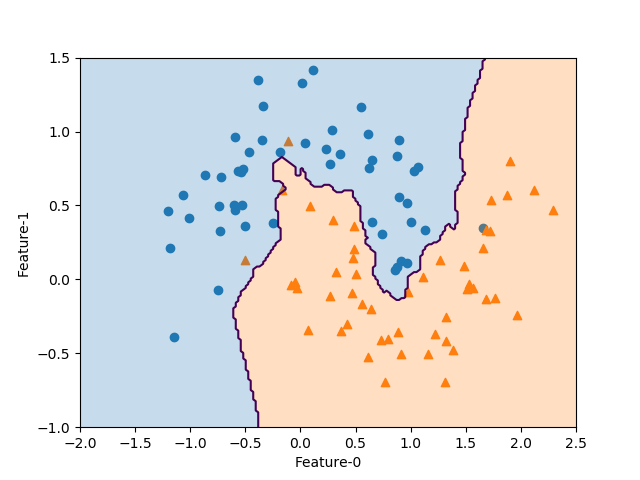
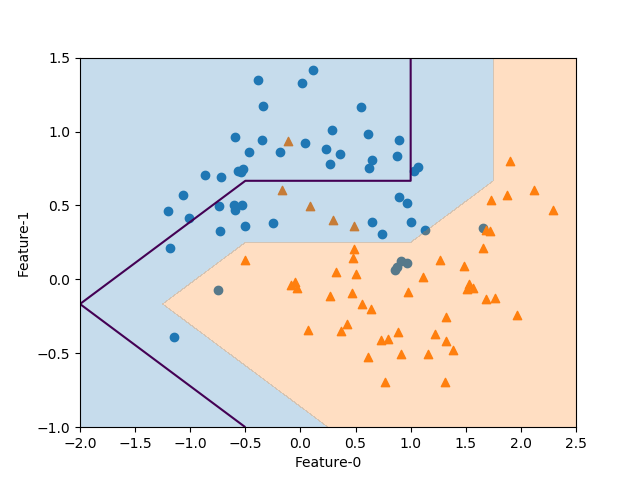
以下はforgeデータセットに対して、カーネルトリックを用いたSVCを適用した例。直線はLinearSVCによる決定境界で、曲線はガウシアンカーネル(RBF)によるSVCの決定境界で、カーネル関数は以下のような形。

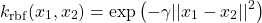
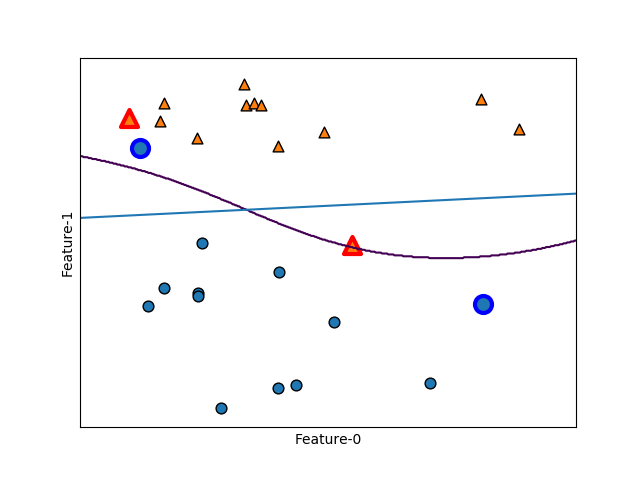
(4) $\begin{equation*} k_{\rm rbf}(x_1, x_2) = \exp \left( -\gamma || x_1 - x_2 ||^2 \right) \end{equation*}$

scikit-learnのSVCの引数で、kernel='rbf'、C=10、gamma=0.1と指定している。

線形モデルの決定境界が直線なのに対して、カーネルトリックによる決定境界は、非線形化した特徴量を導入していることから曲線となっている。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.svm import SVC, LinearSVC

X = np.array( \
[[ 9.96346605,  4.59676542],
 [11.0329545,  -0.16816717],
 [11.54155807,  5.21116083],
 .....
 [ 9.50169345,  1.93824624],
 [ 9.15072323,  5.49832246],
 [11.563957,    1.3389402 ]]
)
y = np.array( \
[1, 0, 1, 0, 0, 1, 1, 0, 1, 1, 1, 1, 0, 0, 1, 1, 1, 0, 0, 1, 0, 0, 0, 0, 1, 0]
)

f0min, f0max = 7.5, 12.5
f1min, f1max = -1, 6

linsvc = LinearSVC(max_iter=4000).fit(X, y)
intercept = linsvc.intercept_
coef = linsvc.coef_.ravel()

svc = SVC(kernel='rbf', C=10, gamma=0.1).fit(X, y)
u = np.linspace(f0min, f0max, 400)
v = np.linspace(f1min, f1max, 400)
u, v = np.meshgrid(u, v)
pred = svc.predict(np.c_[u.ravel(), v.ravel()]).reshape(u.shape)

fig, ax = plt.subplots()

ax.scatter(X[y==0][:, 0], X[y==0][:, 1],
    marker='o', s=60, fc='tab:blue', ec='k')
ax.scatter(X[y==1][:, 0], X[y==1][:, 1],
    marker='^', s=60, fc='tab:orange', ec='k')

sv_class = y[svc.support_]
ax.scatter(svc.support_vectors_[sv_class==0][:, 0],
           svc.support_vectors_[sv_class==0][:, 1],
           marker='o', s=150, fc='tab:blue', ec='blue', linewidth=3)
ax.scatter(svc.support_vectors_[sv_class==1][:, 0],
           svc.support_vectors_[sv_class==1][:, 1],
           marker='^', s=150, fc='tab:orange', ec='red', linewidth=3)

f1 = lambda f0: -(intercept + coef[0]*f0) / coef[1]
ax.plot([f0min, f0max], [f1(f0min), f1(f0max)])

ax.contour(u, v, pred, levels=[0.5])

ax.set_xlim(f0min, f0max)
ax.set_ylim(f1min, f1max)
ax.tick_params(bottom=False, left=False, labelbottom=False, labelleft=False)
ax.set_xlabel("Feature-0")
ax.set_ylabel("Feature-1")

plt.show()

import numpy as np

import matplotlib.pyplot as plt

from sklearn.svm import SVC, LinearSVC

X = np.array( \

[[ 9.96346605, 4.59676542],

[11.0329545, -0.16816717],

[11.54155807, 5.21116083],

.....

[ 9.50169345, 1.93824624],

[ 9.15072323, 5.49832246],

[11.563957, 1.3389402 ]]

)

y = np.array( \

[1, 0, 1, 0, 0, 1, 1, 0, 1, 1, 1, 1, 0, 0, 1, 1, 1, 0, 0, 1, 0, 0, 0, 0, 1, 0]

)

f0min, f0max = 7.5, 12.5

f1min, f1max = -1, 6

linsvc = LinearSVC(max_iter=4000).fit(X, y)

intercept = linsvc.intercept_

coef = linsvc.coef_.ravel()

svc = SVC(kernel='rbf', C=10, gamma=0.1).fit(X, y)

u = np.linspace(f0min, f0max, 400)

v = np.linspace(f1min, f1max, 400)

u, v = np.meshgrid(u, v)

pred = svc.predict(np.c_[u.ravel(), v.ravel()]).reshape(u.shape)

fig, ax = plt.subplots()

ax.scatter(X[y==0][:, 0], X[y==0][:, 1],

marker='o', s=60, fc='tab:blue', ec='k')

ax.scatter(X[y==1][:, 0], X[y==1][:, 1],

marker='^', s=60, fc='tab:orange', ec='k')

sv_class = y[svc.support_]

ax.scatter(svc.support_vectors_[sv_class==0][:, 0],

svc.support_vectors_[sv_class==0][:, 1],

marker='o', s=150, fc='tab:blue', ec='blue', linewidth=3)

ax.scatter(svc.support_vectors_[sv_class==1][:, 0],

svc.support_vectors_[sv_class==1][:, 1],

marker='^', s=150, fc='tab:orange', ec='red', linewidth=3)

f1 = lambda f0: -(intercept + coef[0]*f0) / coef[1]

ax.plot([f0min, f0max], [f1(f0min), f1(f0max)])

ax.contour(u, v, pred, levels=[0.5])

ax.set_xlim(f0min, f0max)

ax.set_ylim(f1min, f1max)

ax.tick_params(bottom=False, left=False, labelbottom=False, labelleft=False)

ax.set_xlabel("Feature-0")

ax.set_ylabel("Feature-1")

plt.show()

scikit-learnのSVCクラスには、サポートベクターに関する以下のパラメーターがある。

support_：データセットにおけるサポートベクターのインデックス（1次元配列）
support_vector_：サポートベクターの配列（2次元配列）

38～44行目で、これらのパラメーターを使ってサポートベクターを強調表示している。

パラメータ調整

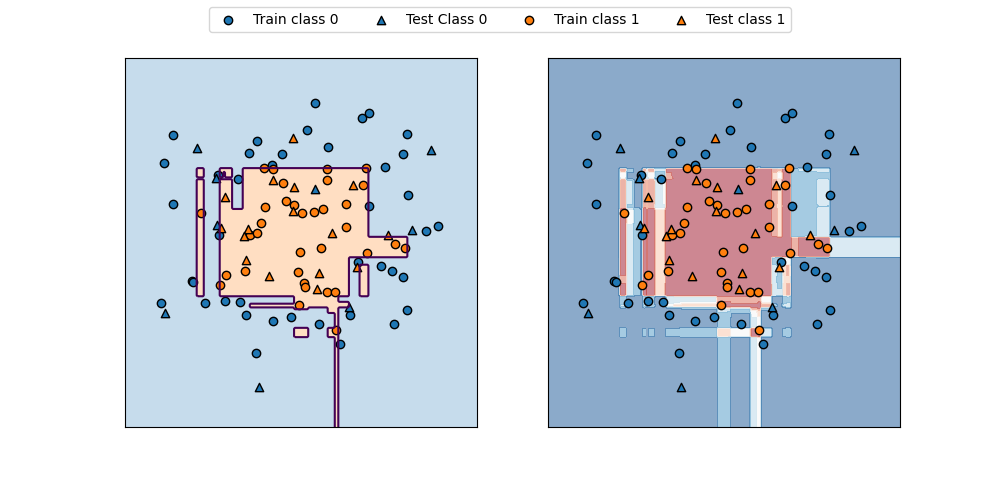
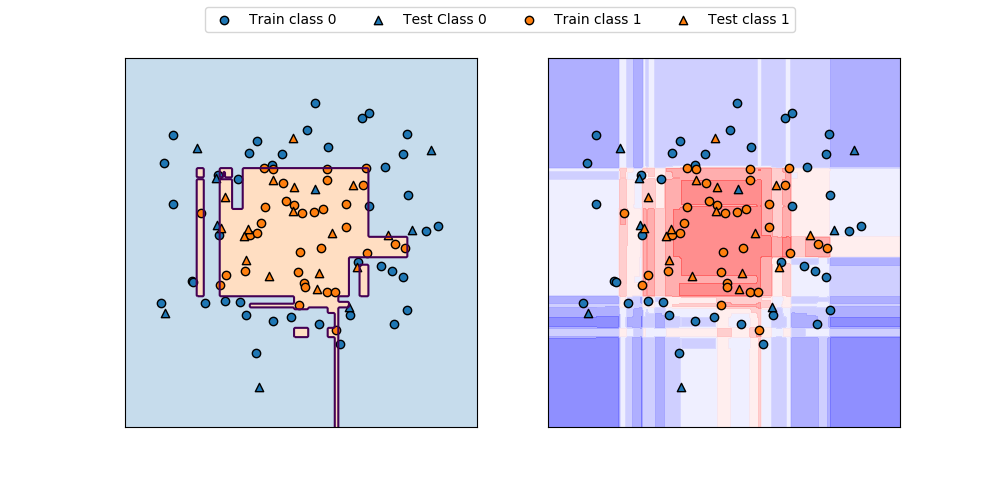
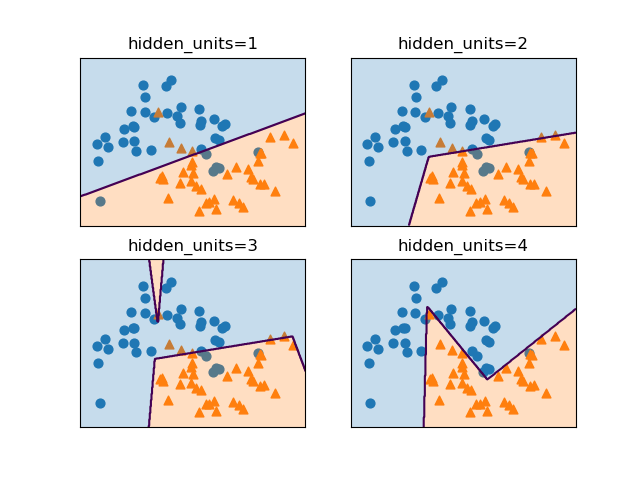
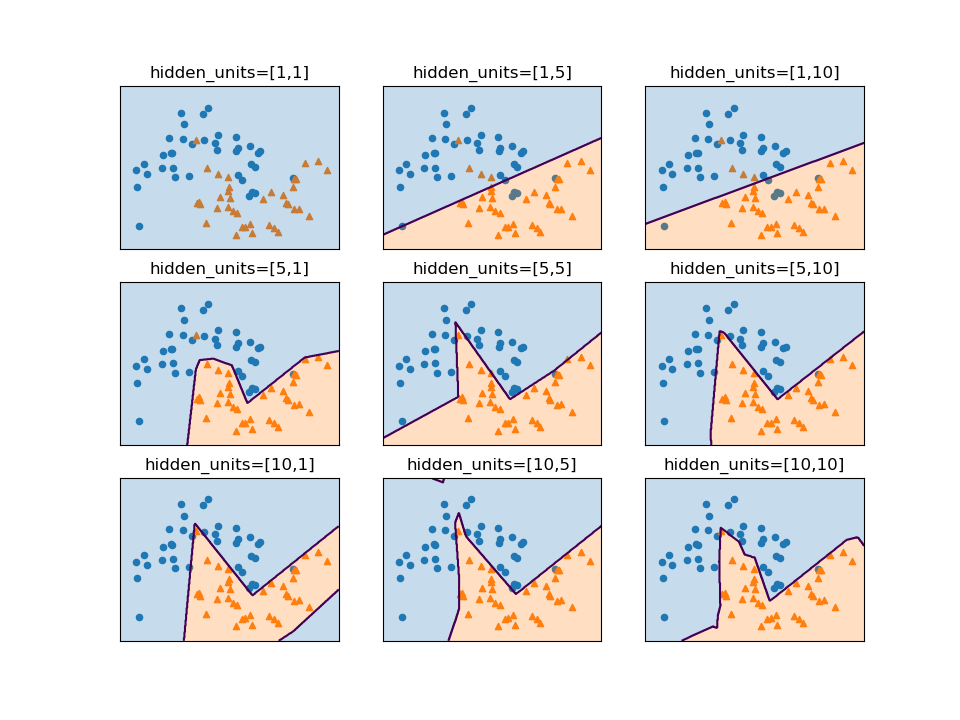
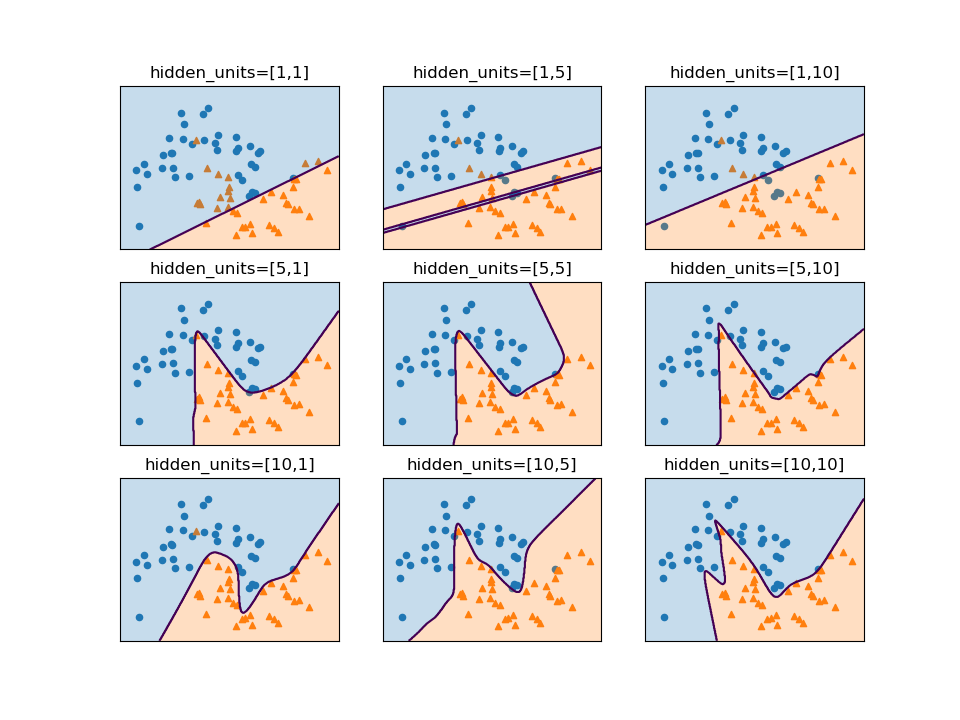
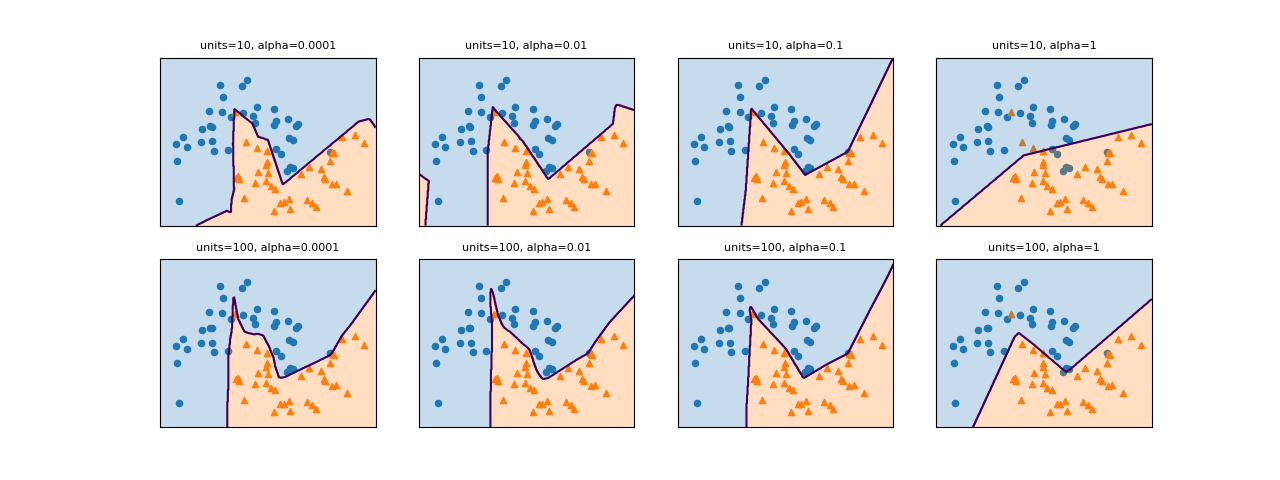
SVCモデルでパラメーターCとgammaの値を変化させたときの決定境界は以下の通り。

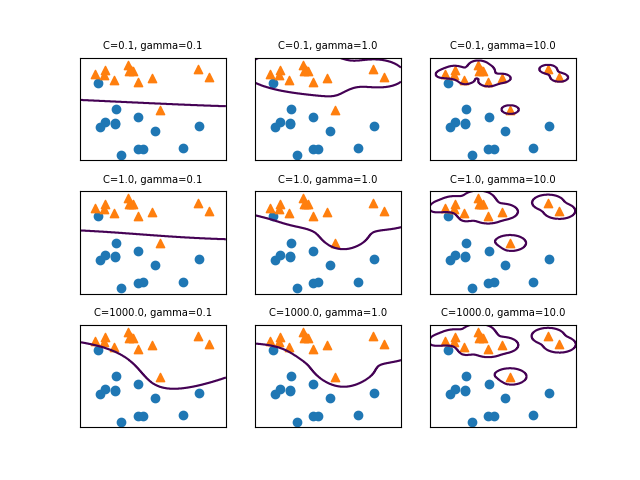
gammaはガウシアンカーネルの直径（σ2に相当）の逆数で、この値が小さいと直径が大きくなり、より多くの点を近いと判断するようになる。左の方はgammaが小さく広域のデータをまとめようとするため、決定境界は大まかとなり、右の方はgammaが大きく近いもの同士をまとめようとする傾向となる。

Cは正則化の強さの逆数で、上の方ほどCの値が小さく正則化が強く効くため、決定境界はよりまっすぐとなり、下の方ほど正則化が弱く個々のデータの影響を受ける。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.svm import SVC
from itertools import product

X = np.array( \
[[ 9.96346605,  4.59676542],
 [11.0329545,  -0.16816717],
 [11.54155807,  5.21116083],
 .....
 [ 9.50169345,  1.93824624],
 [ 9.15072323,  5.49832246],
 [11.563957,    1.3389402 ]]
)
y = np.array( \
[1, 0, 1, 0, 0, 1, 1, 0, 1, 1, 1, 1, 0, 0, 1, 1, 1, 0, 0, 1, 0, 0, 0, 0, 1, 0]
)

f0min, f0max = 7.5, 12.5
f1min, f1max = -1, 6
u = np.linspace(f0min, f0max, 400)
v = np.linspace(f1min, f1max, 400)
u, v = np.meshgrid(u, v)

C_list = [0.1, 1, 1000]
gamma_list = [0.1, 1, 10]
params = product(C_list, gamma_list)

plt.rcParams['font.size'] = 6
fig, axs = plt.subplots(3, 3, figsize=(6.4, 4.8))
axs_1d = axs.ravel()
fig.subplots_adjust(hspace=0.3)

for ax, param in zip(axs_1d, params):
    svc = SVC(kernel='rbf', C=param[0], gamma=param[1]).fit(X, y)
    pred = svc.predict(
            np.hstack([u.ravel().reshape(-1, 1), v.ravel().reshape(-1, 1)])
        ).reshape(u.shape)
    ax.scatter(X[y==0][:, 0], X[y==0][:, 1], marker='o')
    ax.scatter(X[y==1][:, 0], X[y==1][:, 1], marker='^')
    ax.contour(u, v, pred, levels=[0.5])
    ax.tick_params(left=False, bottom=False, labelleft=False, labelbottom=False)
    ax.set_title("C={:.1f}, gamma={:.1f}".format(param[0], param[1]))

plt.show()

import numpy as np

import matplotlib.pyplot as plt

from sklearn.svm import SVC

from itertools import product

X = np.array( \

[[ 9.96346605, 4.59676542],

[11.0329545, -0.16816717],

[11.54155807, 5.21116083],

.....

[ 9.50169345, 1.93824624],

[ 9.15072323, 5.49832246],

[11.563957, 1.3389402 ]]

)

y = np.array( \

[1, 0, 1, 0, 0, 1, 1, 0, 1, 1, 1, 1, 0, 0, 1, 1, 1, 0, 0, 1, 0, 0, 0, 0, 1, 0]

)

f0min, f0max = 7.5, 12.5

f1min, f1max = -1, 6

u = np.linspace(f0min, f0max, 400)

v = np.linspace(f1min, f1max, 400)

u, v = np.meshgrid(u, v)

C_list = [0.1, 1, 1000]

gamma_list = [0.1, 1, 10]

params = product(C_list, gamma_list)

plt.rcParams['font.size'] = 6

fig, axs = plt.subplots(3, 3, figsize=(6.4, 4.8))

axs_1d = axs.ravel()

fig.subplots_adjust(hspace=0.3)

for ax, param in zip(axs_1d, params):

svc = SVC(kernel='rbf', C=param[0], gamma=param[1]).fit(X, y)

pred = svc.predict(

np.hstack([u.ravel().reshape(-1, 1), v.ravel().reshape(-1, 1)])

).reshape(u.shape)

ax.scatter(X[y==0][:, 0], X[y==0][:, 1], marker='o')

ax.scatter(X[y==1][:, 0], X[y==1][:, 1], marker='^')

ax.contour(u, v, pred, levels=[0.5])

ax.tick_params(left=False, bottom=False, labelleft=False, labelbottom=False)

ax.set_title("C={:.1f}, gamma={:.1f}".format(param[0], param[1]))

plt.show()

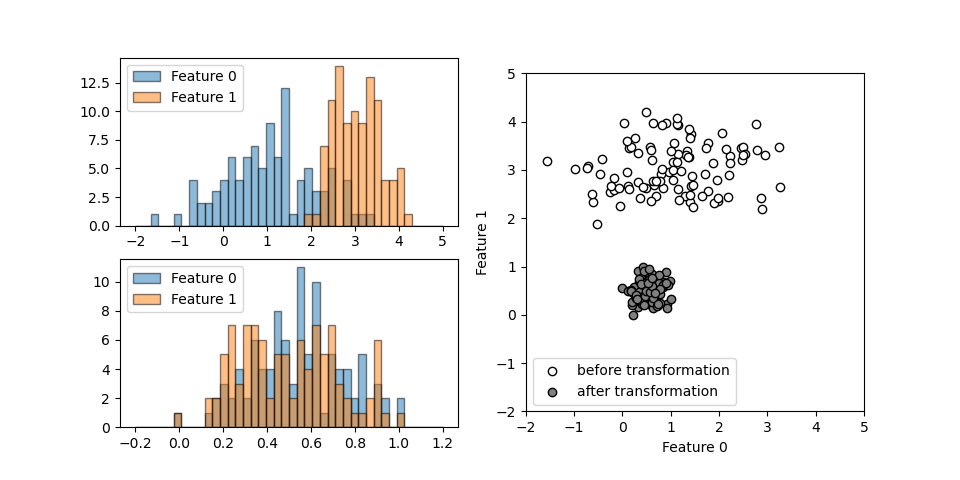
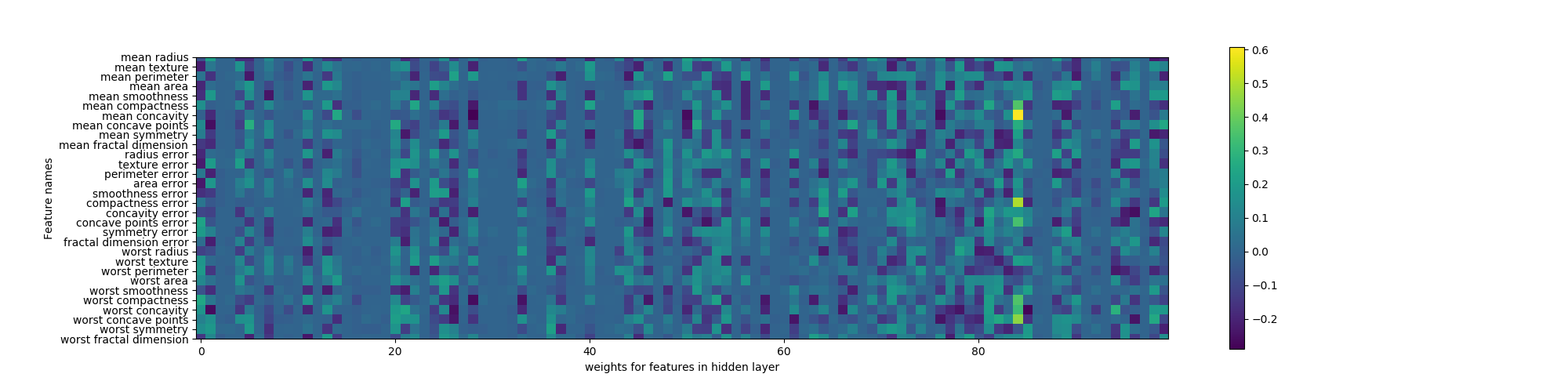
Breast cancerデータへの適用例

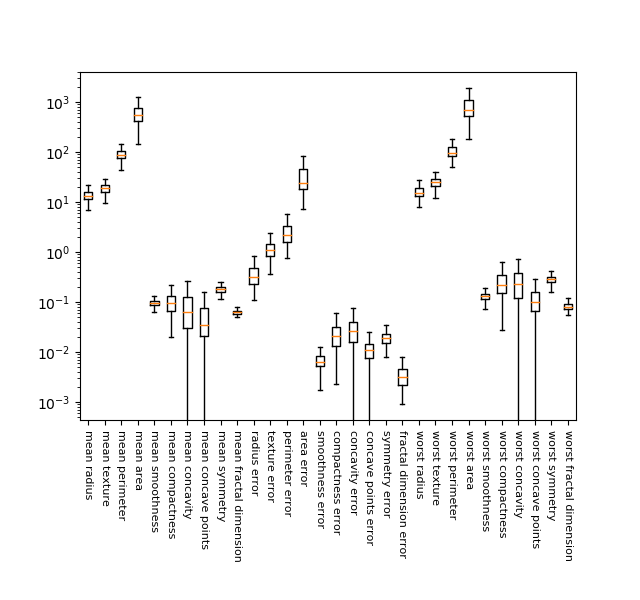
Breast cancerデータへの適用例で、特徴量データの大きさやレンジが大きくばらついていること、特徴量データをそのまま使った場合に過学習となること、特徴量データに前処理を施して正規化(normalize)した場合に精度が向上することを示している。

SVMの特徴

SVMの特徴量を受け売りのまままとめておく。

データにわずかな特徴量しかない場合も複雑な決定境界を生成可能（低次元でも高次元でもうまく機能）
サンプルの個数が大きくなるとうまく機能しない（10万サンプルくらいになると、実行時間やメモリ使用量の面で難しくなる
注意深いデータの前処理とパラメーター調整が必要
検証が難しい（予測に対する理由を理解することが難しい）
RBFの場合、Cやgammaを大きくするとより複雑なモデルになる（2つのパラメーターは強く相関するため、同時に調整する必要がある）

今後の課題～覚え書き

カーネル関数

(5) $\begin{equation*} K(\boldsymbol{x}_1, \boldsymbol{x}_2) = \sum \phi(\boldsymbol{x}_1) \phi(\boldsymbol{x}_2) \end{equation*}$

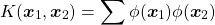
多項式カーネル

(6) $\begin{equation*} K(\boldsymbol{x}_1, \boldsymbol{x}_2) = (\boldsymbol{x}_1 \cdot \boldsymbol{x}_2 + 1 )^d \end{equation*}$

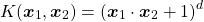
ガウシアンカーネル

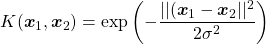
(7) $\begin{equation*} K(\boldsymbol{x}_1, \boldsymbol{x}_2) = \exp \left(- \frac{||(\boldsymbol{x}_1 - \boldsymbol{x}_2 ||^2}{2\sigma^2} \right) \end{equation*}$

SVMの定式化

2020-06-24 / tau / コメントする

SVMの定式化

SVMのクラス分類の条件

2つの特徴量を持つデータが2つのクラスに分かれているとする。ここで下図のように、1つの直線によって、2つのクラスを完全に分離できるとする。

このとき、直線lによって分割したとして、以下の符号によってクラスを分離する。

(1) $\begin{equation*} \left\{ \begin{align} a x_1 + b x_2 + c > 0 &\rightarrow \rm{Class1} \\ a x_1 + b x_2 + c < 0 & \rightarrow \rm{Class2} \end{align} \right. \end{equation*}$

ここでラベル変数t_iを導入する。t_iはデータiがClass1/2のいずれに属するかを示す変数で、Class1ならt_i > 0、Class2ならt_i < 0と定義する。

(2) $\begin{equation*} \left\{ \begin{array}{lll} t_i = 1 & x_i \in \rm{Class1} & (a x_{i1} + b x_{i2} + c > 0) \\ t_i = -1 & x_i \in \rm{Class2} & (a x_{i1} + b x_{i2} + c < 0) \\ \end{array} \right. \end{equation*}$

このラベル変数を用いて、クラスの条件式は以下のように統一される。

(3) $\begin{equation*} t_i (a x_{i1} + b x_{i2} + c) > 0 \end{equation*}$

SVMにおいては、すべてのデータについてこの式が満足されるようにa, b, cを決定する。これらはすべてa, b, cに対する制約条件だが、どのようにこれらの値を求めるべきか、その目的関数が必要になる。SVMでは、これをマージン最大化により行う。

マージン最大化

ある直線l₁によって、下図のようにデータセットがClass1/2に分類できるとする。このときl₁に対してClass1/2の最も直線に近いデータを”サポートベクター”と呼ぶ。また、これらのサポートベクターに対応するl₁と平行な直線間の距離を”マージン”と呼ぶ。

ところで、l₁とは異なる別の直線l₂を選ぶと、異なるサポートベクターに対してより大きなマージンを得ることができる。SVMでは、式(3)のもとでこのマージンを最大化するような直線lを探すこととなる。

直線lに対するサポートベクターの対を(x⁺, x⁻)とすると、それぞれからlへの距離dは以下のように表現される。

(4) $\begin{equation*} d = \frac{|a x^+_1 + b x^+_2 + c|}{a^2 + b^2} = \frac{|a x^-_1 + b x^-_2 + c|}{a^2 + b^2} \end{equation*}$

ここで直線lはマージンの端にある平行な2つの直線の中央にあることから、上式の分子は同じ値となる。この値でdを除したものを改めて $\tilde{d}$ と置くと、dの最大化問題は $1/\tilde{d}=\sqrt{a^2+b^2}$ の最小化問題となる。これに式(3)の制約条件を加味して、問題は以下の制約条件付き最小化問題となる。

(5) $\begin{align*} \min a^2 + b^2 \quad {\rm s.t.} \; t_i (a x_{i1} + b x_{i2} + c) > 0 \; (i=1~n) \end{align*}$

今後の課題

ここから先の定式化
ソフトマージンの導出

概要

挙動

特徴

概要

predict_proba()の挙動

decision_function()との比較

決定境界

3クラス以上の場合

概要

decision_function()の挙動

decision_function()の意味

3クラス以上の場合

概要

得られるデータの形式

パラメーターの指定

利用例

線形モデルの多層化

非線形活性化関数

ニューラルネットワークのチューニング

two moonsデータでの確認

隠れユニット数と決定境界

隠れ層の数

活性化関数tanh

正則化

ランダムな重みづけの影響

データの前処理等

今後の課題

精度不足

データの標準化

random_stateが違う？

重み係数の分布

過学習？

特徴量データのサイズの違い

データの前処理

パラメーター調整

概要

線形特徴量の非線形化

線形モデルでは分離不可能なデータ

非線形特徴量の追加

元の特徴量に対する決定境界

カーネルトリック

概要

パラメータ調整

Breast cancerデータへの適用例

SVMの特徴

今後の課題～覚え書き

SVMの定式化

SVMのクラス分類の条件

マージン最大化

今後の課題

`predict_proba()`の挙動

`decision_function()`との比較

`decision_function()`の挙動

`decision_function()`の意味