感度＝陽性的中率の特性

1 概要
2 指標
3 PPV・NPVの計算式の導出
- 3.1 元データの構成
- 3.2 PPV・NPVの計算式
4 パラメーターに応じたPPV・NPVの変化
5 シミュレーションによる挙動確認

概要

機械学習のモデルの性能や感染症検査の確からしさを検証する際、陽性的中率（適合度）や陰性的中率を確認すべきだが、これらの値が、そもそものデータの特性やモデル／検査の性能によってどのように変化するかを確認する。

具体的には、注目事象の率と真陽性率（感度）・真陰性率（特異度）を変化させたときの、陽性的中率・陰性的中率の変化を見る。

これらの値の意味や計算方法については、Confusing matrixを参照。

その結果から、以下のようなことがわかった。

予測モデルや検査において、単に感度のみを向上させても適合度（陽性的中率）は大きく変化しない
特異度を向上させることで適合度は大きく向上する
ターゲット比率がとても小さい場合、感度・特異度をかなり大きくしても、適合度は小さな値になる

2020年現在、世界的に大きな影響を及ぼしているCOVID-19（新型コロナウィルス）感染症のPCR検査では、一般に感度が70％程度、特異度が90％以上、陽性的中率が数%程度という値が多い。感度が7割程度というのは少し低く、陽性的中率がそもそも小さすぎるという気がしていたが、上記のことと符合することがわかった。

指標

以下の指標を、目的として計算する指標とする。

PPV(Positive Predicted Value)：陽性的中率、適合度、Precision
NPV(Negative Predicted Value)：陰性的中率

これらの指標を計算するために用いる指標は以下の通り。

TR(Target Rate)：注目事象の全体比率（ターゲット比率）
TPR(True Positive Rate)：真陽性率、感度(Sencitivity)
TNR(True Negative Rate)：真陰性率、特異度(Specificity)

例えば感染症の例で言うと、有病率(TR)、検査の感度(TPR)、特異度(TNR)がわかっているときに、陽性的中率(PPV)、陰性的中率(NPV)を求めることに相当する。

PPV・NPVの計算式の導出

元データの構成

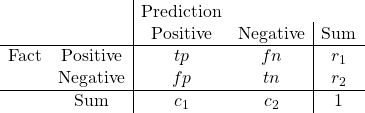
まず、confusing matrixを以下のように表現する。これは、データ数で表現されたテーブルの各要素を全データ数で割った率で表すことに相当する。

$\begin{align*} \begin{array}{cc|cc|c} & & \mathrm{Prediction}\\ & & \mathrm{Positive} & \mathrm{Negative} & \mathrm{Sum} \\ \hline \mathrm{Fact} & \mathrm{Positive} & tp & fn & r_1 \\ & \mathrm{Negative} & fp & tn & r_2 \\ \hline & \mathrm{Sum}& c_1 & c_2 & 1 \end{array} \end{align}$

PPV・NPVの計算式

まず、事実(Fact)がpositiveである率がr₁に相当し、これはTR (target rate)に等しい。このTRと率TPRを使って、Positiveの行のtp(true positive)とfn (false negative)の率を計算。

(1) $\begin{align*} r_1 &= TR \\ tp &= r_1 \cdot TPR = TR \cdot TPR \\ fn &= r_1 \cdot (1 - TPR) = TR (1 - TPR) \end{align*}$

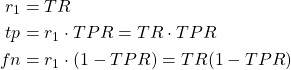
2行目の合計r₂については、行和の合計が1になることから以下のように計算される。

(2) $\begin{align*} r_2 &= 1 - r_1 = 1 - TR \end{align*}$

このr₂と率TNRからNegativeの行のtn(true negative)とfp (false positive)を計算。

(3) $\begin{align*} tn &= r_2 \cdot TNR = (1 - TR) TNR \\ fp &= r_2 (1 - TNR) = (1 - TR) (1 - TNR) \end{align*}$

tpとfpからc₁を、tnとfnからc₂を計算。

(4) $\begin{align*} c_1 &= tp + fp = TR \cdot TPR + (1 - TR) (1 - TNR) \\ c_2 &= tn + fn = (1 - TR) TNR + TR (1 - TPR) \end{align*}$

PPV（陽性的中率、感度）はc₁に対するtpの率で計算される。以下の式は分数の分数で若干ややこしいが、3つの指標が1回ずつ現れ、整った形になる。

(5) $\begin{align*} PPV &= \frac{tp}{c_1} = \frac{TR \cdot TPR}{TR \cdot TPR + (1 - TR) (1 - TNR) } \\ &= \frac{1}{1 + \left(\dfrac{1}{TR} - 1 \right) \dfrac{1 - TNR}{TPR}} \end{align*}$

NPV（陰性的中率、特異度）はc₂に対するtnの率で計算される。以下の式とPPVの式を比べると、はTRの分数項ついて逆数であり、TPRとTNRが入れ替わっていて、PPVとNPVで対称性がある。

(6) $\begin{align*} NPV &= \frac{tn}{c_2} = \frac{(1 - TR) TNR}{(1 - TR) TNR + TR (1 - TPR)}\\ &= \frac{1}{1 + \dfrac{TR}{1 - TR} \dfrac{1 - TPR}{TNR}} \end{align*}$

パラメーターに応じたPPV・NPVの変化

PPV

上記の結果を用いて、ターゲット比率、真陽性率（感度）、真陰性率（特異度）の様々な値に対するPPV（陽性的中率）、NPV（陰性的中率の変化を観察する。

まず、ターゲット比率が1に近い（ほとんどがターゲットとなるような）状態から、ターゲットが0に近いような（ターゲットとなるデータがほとんどないような）状態の間で、PPVがどのように変化するか確認してみる。

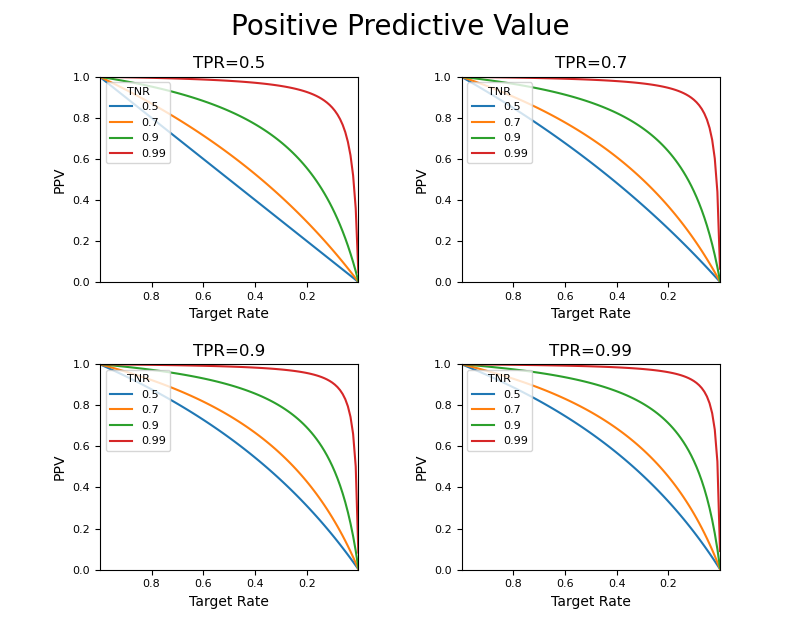
TPR（感度）の値によって曲線の形に若干の変化はあるがあまり大きくは変わらず、むしろTNR（特異度）の値による曲線の形状の変化が大きい。ここでTRが0.1～0と小さい範囲のところを見てみる。

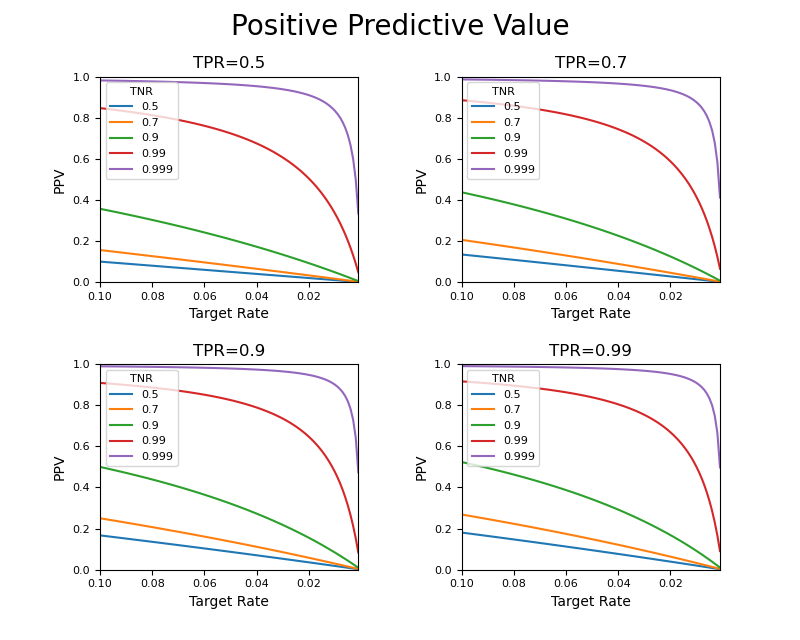
やはり感度の影響はあまり大きくないようである。TNRを大きくするにしたがって曲線の形状は大きく変化し、ターゲット比率が小さいところでの適合度が向上するが、ターゲット比率が0に近いところではPPVがかなり小さくなる。

次に、TPRを変化させたときの曲線の違いが分かるように、表示させる変数を入れ替えてみる。まずTRが1～0の全域。

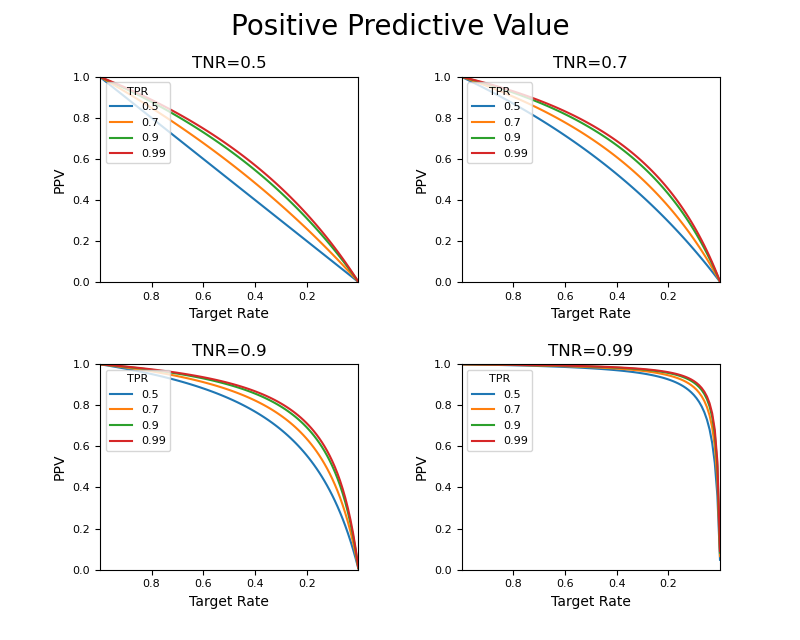
やはり感度による曲線の変化は小さく、特異度の影響が大きい。以下のようにTRが0.1～0の範囲を拡大しても同様の傾向。

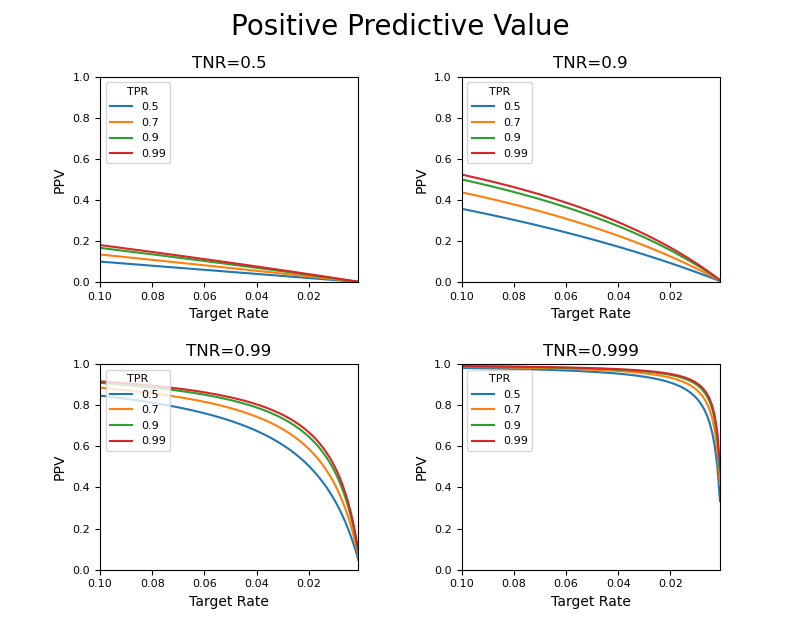
以上の結果から、以下のことが言える。

ターゲット比率が低くなるほどNPVは小さくなる（適合度が低くなり、予測／検査の信頼性が下がる）
予測モデルや検査のTPR（感度）を上げることによるPPVの向上効果はあまり大きくない（いたずらに感度を上げても顕著な効果はない）
TNR（特異度）の向上によって、適合度は大きく向上する
ターゲット比率がとても小さい場合、その率の現象に従って適合度は急激に低下する

さらにこれを一般的な表現でまとめると、

予測モデルや検査において、単に感度のみを向上させても適合度（陽性的中率）は大きく変化しない
特異度を向上させることで適合度は大きく向上する
ターゲット比率がとても小さい場合、感度・特異度をかなり大きくしても、適合度は小さな値になる

NPV

PPVと同様にNPVについても計算してみた。

まずいくつかのTPRに対して、TNRを変化させて曲線を描いたもの。PPVの場合と比べて形状が左右逆で、TNRを固定してTPRを変化させたときの図と同じ傾向。

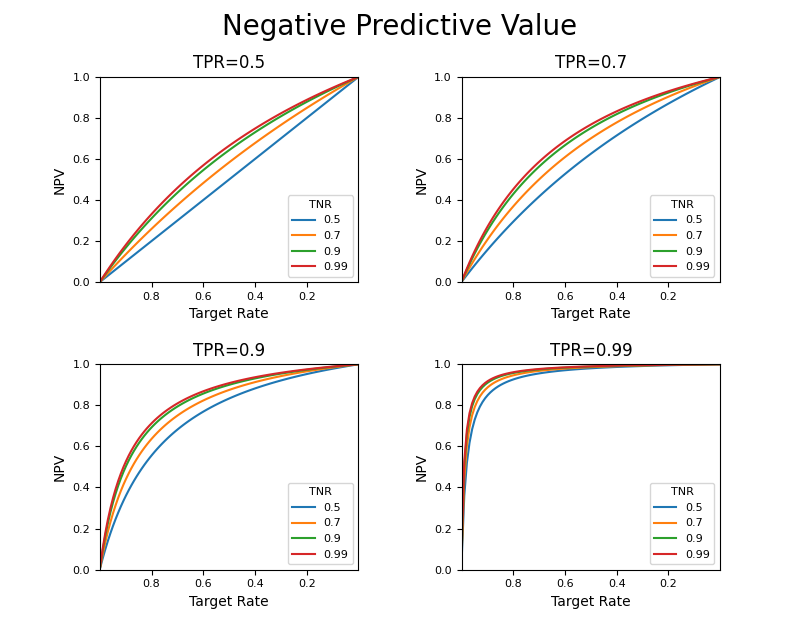
次に、いくつかのTNRを固定してTPRを変化させたもの。これもPPVと形状、TPR、TNRの関係が逆になっている。

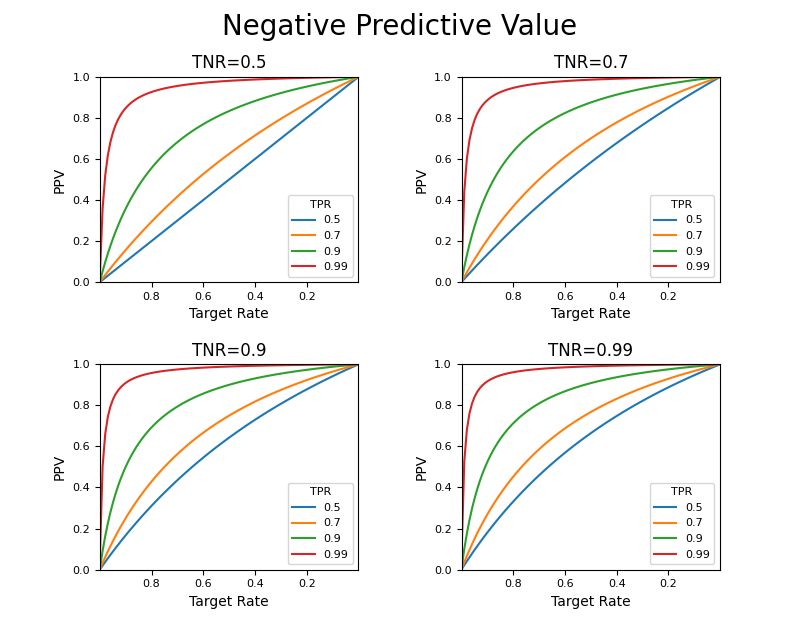
PPVとNPVの関係

PPVとNPVが同じTPR、TNRに対してどのように変化するか重ねてみる。

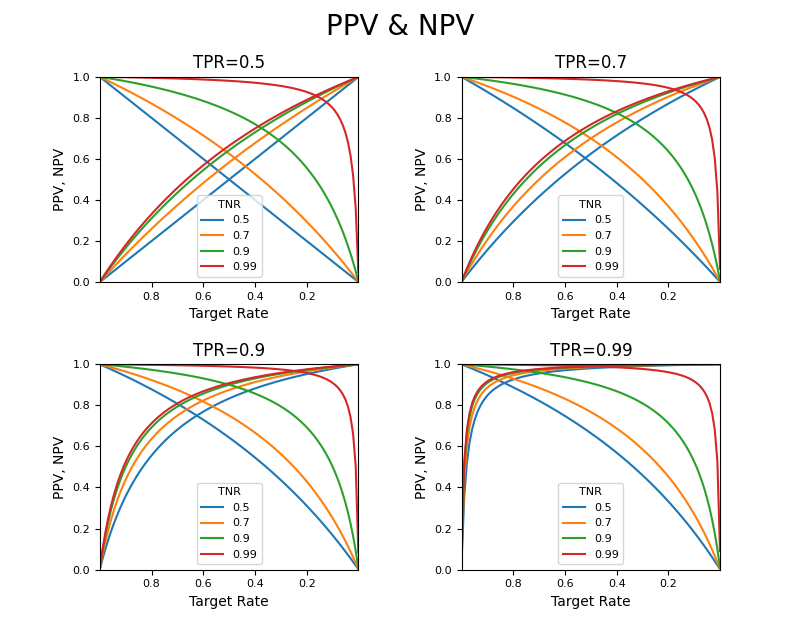
TPRとTNRを同程度とすることでターゲット比率0.5付近で双方が等しくなり、その値を高くすることで、より広い範囲でPPVが向上する。

シミュレーションによる挙動確認

これまでの結果は、confusion matrixの各要素にTR、TPRなどの比率を適用してPPV、NPVを計算した。この方法は、ある予測／判定が理論通りに再現された場合だが、実際にはターゲットとなる事象の割合も、予測がpositive/negativeになる割合も確率事象である。

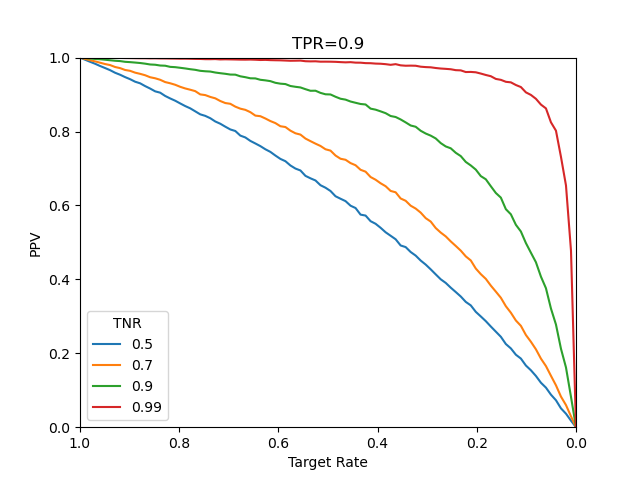
そこで念のため、多数の二値(True/False)正解データをランダムに生成し、これに対してTPR、TNRの設定に従った答えを出す疑似的なモデルで「予測」する。その結果を整理したconfusion_matrixからPPVを計算したのが以下の図である。

その結果は計算式による場合と同じで、理論上の挙動と実世界で起こるであろう挙動が一致している。

処理内容は以下の通り。

与えられたTrue/Falseに対して、あらかじめ設定したTPR/TNRと一様乱数に従ってTrue/Falseを「予測」する疑似予測モデルを準備
TR=1～0の間で100個のデータについてPPVを計算する
- 1つのTRについて10万個の2値正解データを生成
- 正解データセットを疑似予測モデルに適用して予測データセットを得る
- 予測データセットからconfusion matrixを構成し、その要素からPPVを計算し、配列に格納
以上の結果をプロット

import numpy as np
import random as rnd
import matplotlib.pyplot as plt
from sklearn.metrics import confusion_matrix

def generate_data(target_rate=0.5, data_size=1000):
    y = np.empty(data_size, dtype=bool)
    for i in range(data_size):
        y[i] = rnd.random() < target_rate
    return y

class ImitationLearningModel:
    def __init__(self, tpr, tnr):
        self.tpr = tpr
        self.tnr = tnr

    def predict(self, y_fact):
        y_pred = np.empty(y_fact.size, dtype=bool)
        for i in range(y_fact.size):
            if y_fact[i]:
                y_pred[i] = rnd.random() < self.tpr
            else:
                y_pred[i] = rnd.random() > self.tnr
        return y_pred

fig, ax = plt.subplots()

tpr = 0.9
tnrs = [0.5, 0.7, 0.9, 0.99]

n_data = 100
trs = np.linspace(0, 1, n_data)
ppv = np.empty((len(tnrs), trs.size))

for j, tr in enumerate(trs):
    y_fact = generate_data(target_rate=tr, data_size=100000)
    for i, tnr in enumerate(tnrs):
        model = ImitationLearningModel(tpr, tnr)
        y_pred = model.predict(y_fact)
        cfmat = confusion_matrix(y_fact, y_pred, labels=[True, False])
        ppv[i, j] = cfmat[0, 0] / (cfmat[0, 0] + cfmat[1, 0])

for i, tnr in enumerate(tnrs):
    ax.plot(trs, ppv[i], label=tnr)

ax.set_xlim(0, 1)
ax.set_ylim(0, 1)
ax.invert_xaxis()
ax.set_xlabel("Target Rate")
ax.set_ylabel("PPV")
ax.legend()
ax.legend(title="TNR", loc='lower left')
ax.set_title("TPR={}".format(tpr))

plt.show()

import numpy as np

import random as rnd

import matplotlib.pyplot as plt

from sklearn.metrics import confusion_matrix

def generate_data(target_rate=0.5, data_size=1000):

y = np.empty(data_size, dtype=bool)

for i in range(data_size):

y[i] = rnd.random() < target_rate

return y

class ImitationLearningModel:

def __init__(self, tpr, tnr):

self.tpr = tpr

self.tnr = tnr

def predict(self, y_fact):

y_pred = np.empty(y_fact.size, dtype=bool)

for i in range(y_fact.size):

if y_fact[i]:

y_pred[i] = rnd.random() < self.tpr

else:

y_pred[i] = rnd.random() > self.tnr

return y_pred

fig, ax = plt.subplots()

tpr = 0.9

tnrs = [0.5, 0.7, 0.9, 0.99]

n_data = 100

trs = np.linspace(0, 1, n_data)

ppv = np.empty((len(tnrs), trs.size))

for j, tr in enumerate(trs):

y_fact = generate_data(target_rate=tr, data_size=100000)

for i, tnr in enumerate(tnrs):

model = ImitationLearningModel(tpr, tnr)

y_pred = model.predict(y_fact)

cfmat = confusion_matrix(y_fact, y_pred, labels=[True, False])

ppv[i, j] = cfmat[0, 0] / (cfmat[0, 0] + cfmat[1, 0])

for i, tnr in enumerate(tnrs):

ax.plot(trs, ppv[i], label=tnr)

ax.set_xlim(0, 1)

ax.set_ylim(0, 1)

ax.invert_xaxis()

ax.set_xlabel("Target Rate")

ax.set_ylabel("PPV")

ax.legend()

ax.legend(title="TNR", loc='lower left')

ax.set_title("TPR={}".format(tpr))

plt.show()

TauStation

感度＝陽性的中率の特性

概要

指標