Confusion Matrix～混同行列

/ tau / コメントする

概要

精度が高いのに性能が悪い？

クラス分類の機械学習の結果、全体の精度のほか、注目しているクラスの分類性能などについて確認しておく必要がある。

たとえば製造部品の良／不良を判別するケースで不良品の確率が1/1000などとても小さい場合や、疾病の判定をするケースで罹患する率が1万人に1人と非常に低い場合を考えてみる。

求めているのは、僅かに発生する不良品を選りだすことや、稀に罹患している人を特定することだ。このとき、ターゲットでない（正常品や罹患していない）多数のクラスを正確に分類できれば全体の正解率は上がる。ところがその一方で、求めている事象（不良品や罹患者の）ターゲットの分類精度が低いと、正解率には影響しないが本来求めているターゲットの分類機能としては低くなる。

誤判定の度合い

このほか、疾病に罹患していると判定したのに実際には罹患していない場合や、罹患していないと判定したのに実は罹患している場合など、分類器の誤判定の度合いも重要だ。

間違ってターゲットを特定してもいいから漏れがないようにしたいのか、誤って特定するリスクを避けたいのか、それらをもちいるケースに応じて分類器の性能がどうあるべきかを検討する必要がある。

confusion matrixの活用

このような場合にもちいられるのがconfusion matrixである。それは機械学習において用いられるテーブルで、クラス分類のターゲットクラスと予測されたクラスを行と列にとり、各々がどのように一致しているか／異なっているかを示したものである。

その要素と行／列の合計から、予測モデルの性能を示す様々な指標を計算することができる。

Confusion matrixの構成

3クラス分類の例

Confusion matrixは以下のように構成される。

  • 行（または列）に正解のクラス列を、（または行）に予測されたクラスの列を、同じ順番で並べる
  • 各正解クラスに対して、予測されたクラスの数を入れていく

例えば画像認識で果物を判別する予測モデルを考え、りんご、梨、洋梨の3つのクラスを分類するものとする。このとき、ある予測を行った結果として得られたconfusion matrixの一例を示す。

行の側に正解（事実）、列の側に予測（判定）を置いているが、この定義は場合によって入れ替わる（Scikit-learnのライブラリーではこれと同じ配置だが、WikipediaのConfusion matrixの解説では逆になっている）。

予測
りんご 梨 洋梨 計
正解 りんご   80   15   5   100
梨   27   70   3   100
洋梨   2   3   95   100
計   109   88   103   300

2クラス分類での一般化

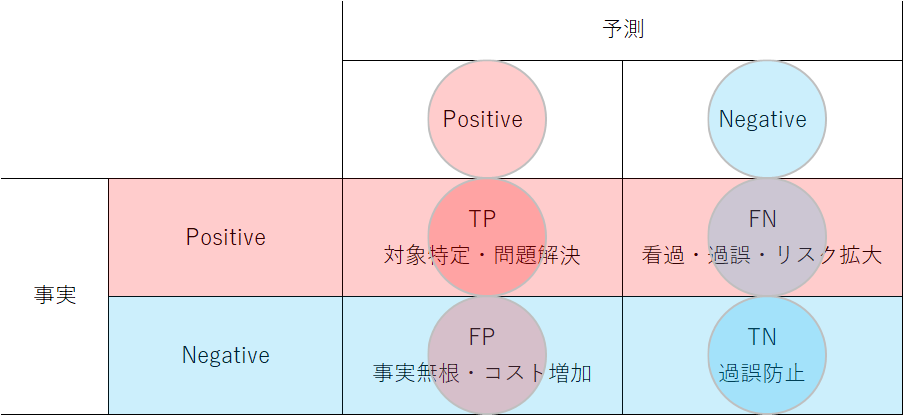
左記の果物のconfusion matrixは3クラス分類の例だが、以下は2クラス分類で考えていく。様々な2クラス分類におけるconfusion matrixの共通した構成を一般化したのが以下の図である。2つのクラスのうち”Positive”と表現しているのが「特に捕捉したい／注目している事象」に分類されるもので、たとえば不良品や疾病の発見、成長企業の特定など。他方はそれ以外で、製造品が正常、被検者が罹患していないといった捕捉の対象としない事象に対応する。

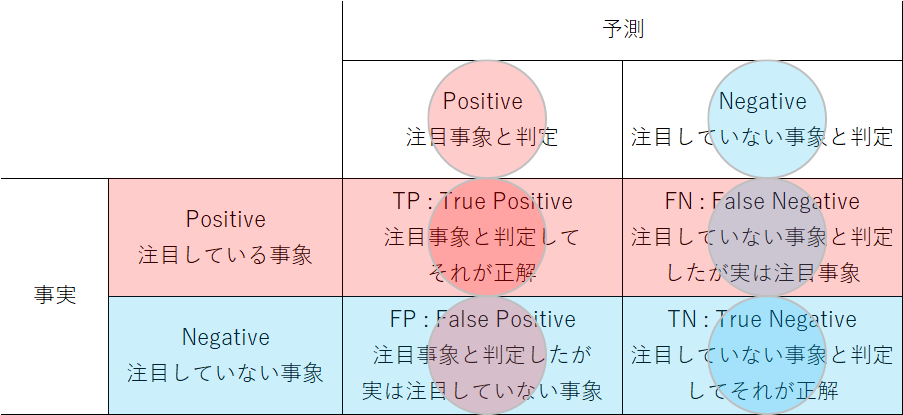
Positiveな事象（注目している事象）について、英語では”relevant instances”などの表現が使われているが、relevantの意味には、直訳の「関連～」だけではなく「重要な」というニュアンスもあるようなので、ここでは「注目」という用語を使う。

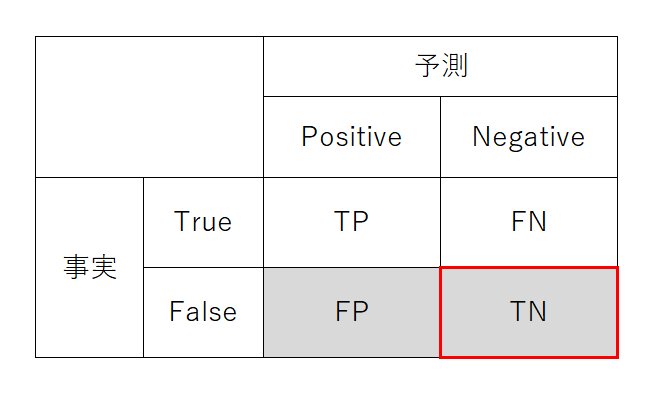
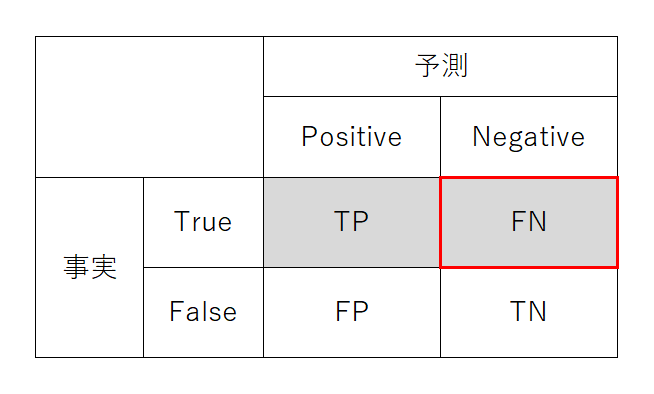
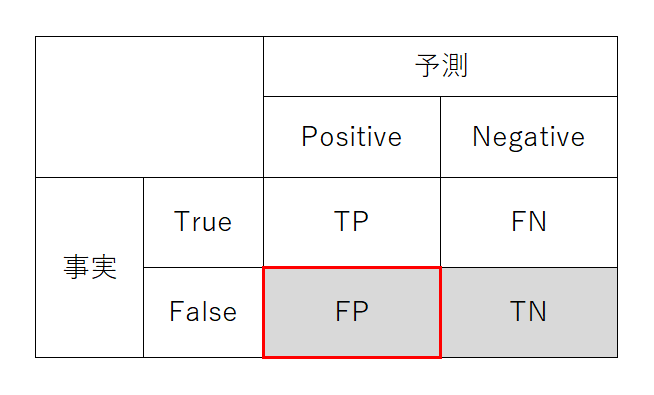
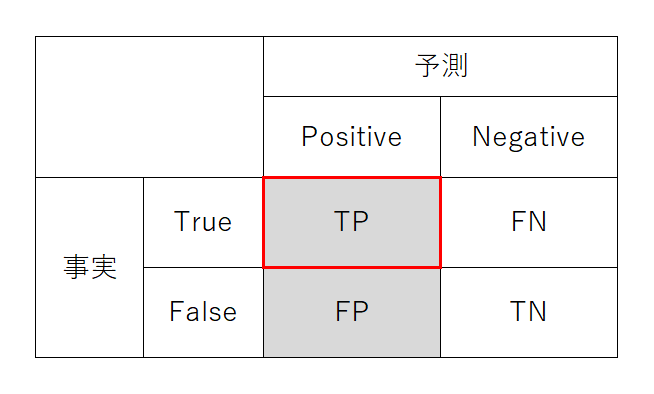
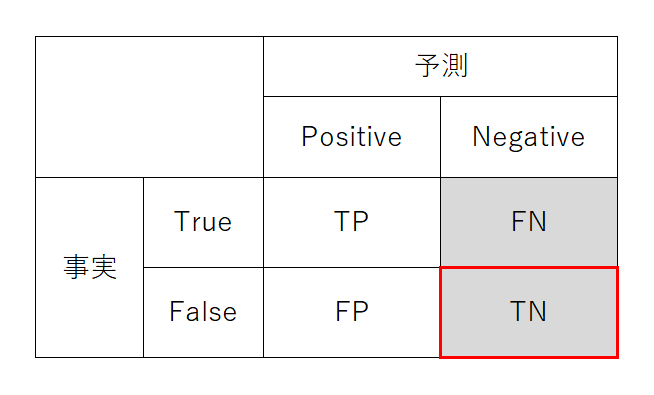
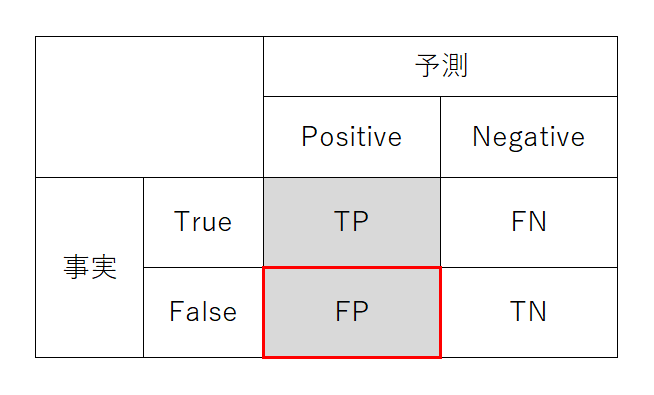
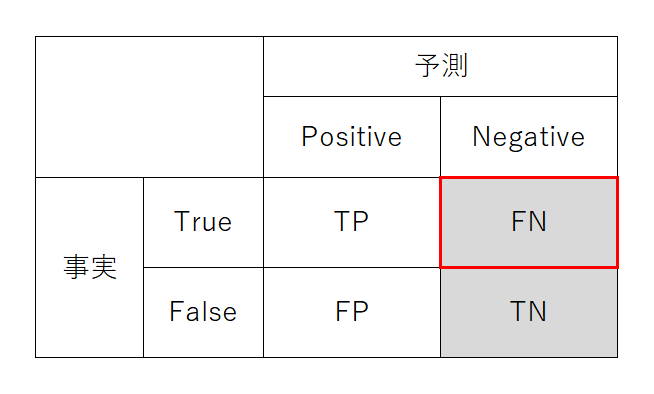
まず表の左上と右下について。予測した事象と実際の事象が一致している場合で色が同じになっている。この場合は予測が正しいという意味でTrueとする。左上はPositive（注目事象）と予測してそれが正しいのでTrue Positive (TP)と呼ぶ。また右下はNegative（注目していない事象）と予測してそれが正しいのでTrue Negative (TN)と呼ぶ。

次に左下と右上について。今度は予測結果の色と事実の色が異なっている。この場合は予測が誤っているという意味でFalseとする。左下はPositiveと予測したが誤りなのでFalse Positive (FP)、一方右上は予測がNegativeだがそれが誤りなのでFalse Negative (FN)と呼ぶ。

True/FalseとPositive/Negativeの順番とテーブル上の位置がややこしいが、常に予測・判定結果から見てそれが事実に対して正しいか誤りかと考えて「正しい／誤った、Positive判定／Negative判定」と定義されている。

Positive/Negativeを疾病検査の陽性(potitive)／陰性(negative)にあてはめると、TP：真陽性、TN：真陰性、FP：偽陽性、FN：偽陰性とも呼ばれる。

2クラス分類の例

疾患検査

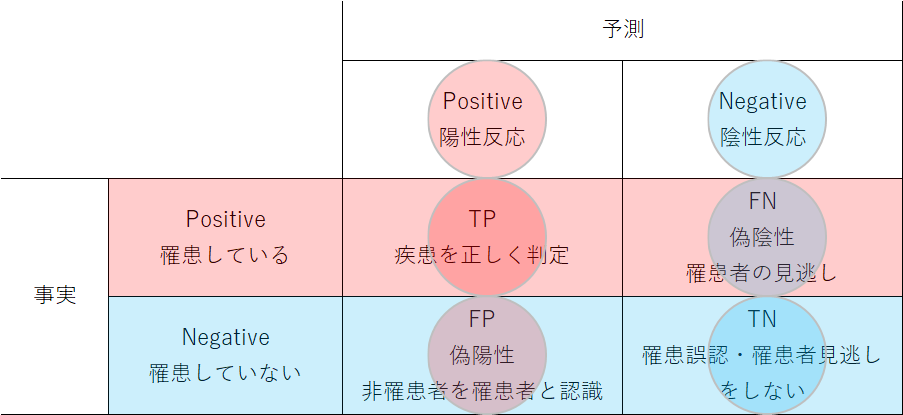
次に2クラス分類の実世界での例を見てみる。まず、よくある例として、ある疾患にかかっているかどうかを検査する例。この場合はまさしく予測が陽性(Positive)か陰性(Negative)かに相当する。FPならば罹患していない人が不要な治療・対応を受けることになり、FNならば罹患している人を見逃すことになる。

犯人特定

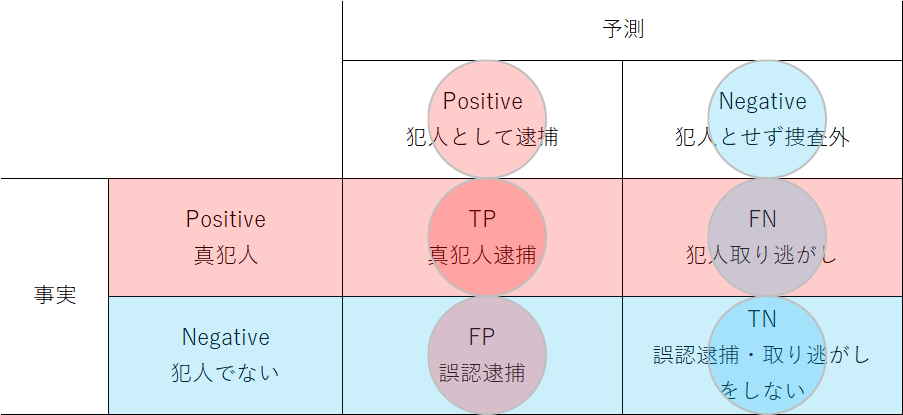
次に、カメラ画像や様々な証拠などから犯人を見つけ出すような問題。対象者が犯人であるという事象に注目して、これをpositiveな判定としている。FPの場合は無実の人の誤認逮捕に結びつき、FNならば犯人を取り逃がすことになる。

ヒット商品予測

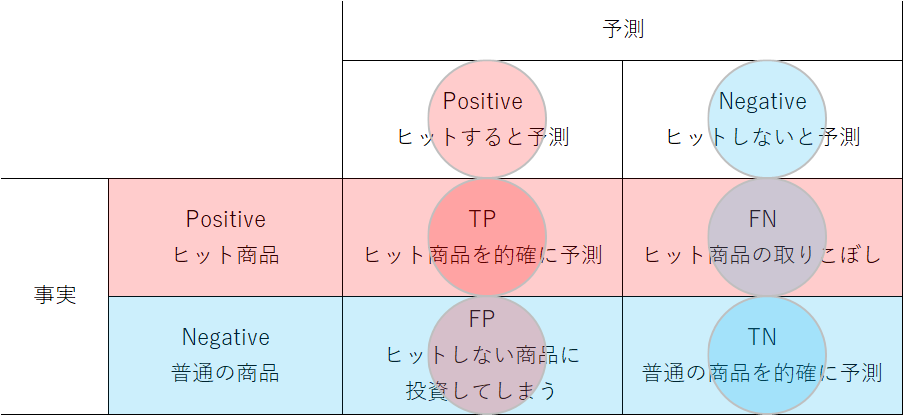
これまでの2つは、どちらかと言えば注目事象がよくない影響を及ぼすものだったが、これがよい効果をもたらす例を考えてみる。以下の例は、開発しようとしている商品がヒットするかどうか、いろいろな情報に基づいて予測しようとするものである。FPならヒットしない商品に無駄な投資をすることになり、FNならばヒット商品の開発の機会を逃すことになる。

4つの象限の意味・結果

これらの例も見ながら、confusion matrixの4つの象限がどのような意味を持つか、以下のように整理してみる。

TP
注目対象を正しく分類する。対処すべき事象が特定できる。
FP
注目すべきでないものを誤って注目対象に分類してしまう。注目対象が好ましくない事象の場合はその対策に余計なコストがかかったり、場合によっては謂れのない差別などの対象となったりする。好ましい事象の場合は、無駄なコストをかけることになる。統計学で言う第2種の過誤にあたる。
TN
注目対象以外のものを正しく分類する。注目対象を誤って見逃すことがなく、被害の拡大や機会損失を避けられる。
FN
注目対象を誤って注目対象以外に分類してしまう。捕捉すべき望ましくないものを見逃して影響が拡大したり、望ましいものを見逃して利得を得る機会を逃したりする。統計学で言う第1種の過誤にあたる。

指標

Confusion matrixの4つの象限の値から、複数の指標が導かれる。それぞれの和名には、時々異なるものを指している例があるので、英語表現を基本にする。

全体に対する率

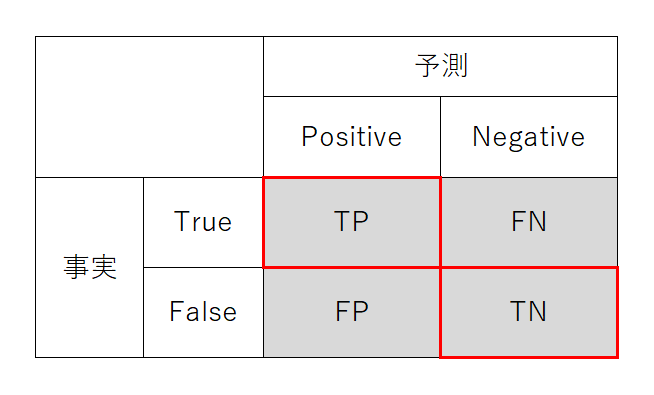
まず、4象限全体（すなわち全データ数）に対する率を考える。これらは注目事象か非注目事象かに関わらない、モデル全体の正確さを表す。

Accuracy（正解率・正確度）

予測結果が正しく注目対象と非注目対象を言い当てた率。4象限の対角要素の合計の、総計に対する率を計算する。様々な機械学習モデルのスコアとして計算される値に相当する。Accuracyは「（ばらつきはともかく）予測が真値をどれだけ（平均的に）言い当てているか」という意味。このAccuracyを「精度」と呼んでいる場合があるが、科学的な表現としては少しずれている。

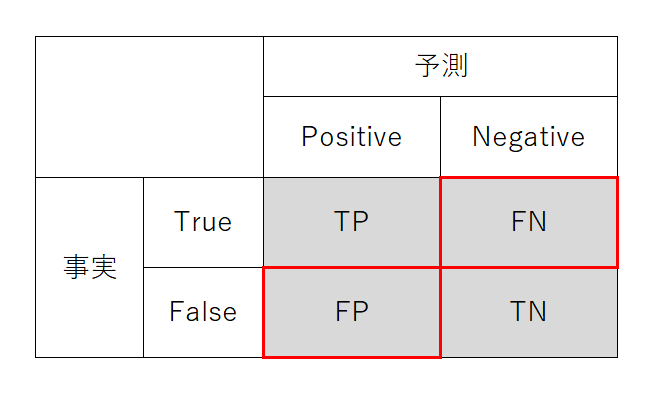
(1)   \begin{equation*} \frac{TP + TN}{TP + FP + FN + TN} \end{equation*}

Error Rate（不正解率）

Accuracyと逆で、予測結果が実際の注目・非注目対象から外れた率。4象限の非対角要素の合計の、総計に対する率として計算する。

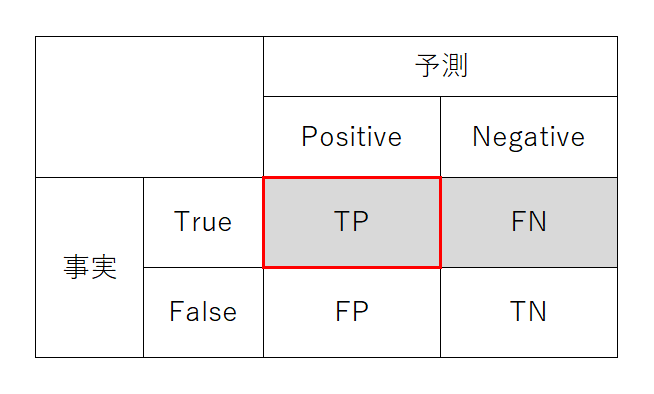
(2)   \begin{equation*} \frac{FP + FN}{TP + FP + FN + TN} \end{equation*}

正解・事実に対する率

表の横方向の、各行それぞれの合計に対する率。正解に対するモデルの正確さを表す。

Sensitivity/Recall/TPR
（感度・再現率・検出率・真陽性率）

正解が注目事象の場合に、モデルも注目事象と分類する率。疾病検査を例にすると、その検査が疾病をとらえる「感度・検出率」となる。TNR(True Positive Rate)：真陽性率については、この後も真～率、偽～率が出てくるが、これらはすべて行方向に対する（正解・事実に関する）予測・分類の正確さと定義される。”recall”のニュアンス（呼び戻す、想起するなど）は、この指標の意味に繋がりにくい。むしろ無理やり日本語にしたような「再現率」の方がまだ本来の意味に近いと感じられる。

(3)   \begin{equation*} TPR = \frac{TP}{TP + FN} \end{equation*}

Specificity/TNR（特異度・真陰性率）

正解が注目していない事象の場合に、モデルがそれを間違いなく分類した率。疾病検査なら、罹患していない人の結果が陰性となる率。「特異度」という訳は”specific”～「特別な」というあたりから名付けたのかもしれないがセンスが悪い。むしろこれは問題ないものを問題ないと分類する率だから、「特異」ではないはずだ。せめてspecify～特定するで「特定率」くらいならまだしもか。TNRはTrue Negative Rate。

(4)   \begin{equation*} TNR = \frac{TN}{FP + TN} \end{equation*}

FNR（偽陰性率）

FNR(False Negative Rate)はTPRの裏で、正解が注目事象なのにそうでないと分類してしまった率。罹患しているのに検査で陰性となる率に相当する。

(5)   \begin{equation*} FNR = 1 - TPR = \frac{FN}{TP + FN} \end{equation*}

FPR（偽陽性率）

FPR(False Positive Rate)はTNRの裏で、正解が注目していない事象なのに注目事象だと判定してしまった率。罹患していないのに検査で陽性だと判定されてしまう率に相当する。

(6)   \begin{equation*} FPR = 1 - TNR = \frac{FP}{FP + TN} \end{equation*}

予測・判定結果に対する率

表の縦方向、各列の合計に対する率。分類結果がどの程度信頼できるかを表す。日本のサイトではPPV、高々NPVまでしか紹介されていないが、英語版のWikipediaではすべて図入りで説明されている。

Precision/PPV（適合度・精度・陽性的中率）

Precision(適合度）はモデルが注目事象と予測した場合に、実際にそれが注目事象である率。疾病検査で陽性判定の場合に実際に罹患している率に相当する。なお、科学上の表現でのprecision（精度）は、本来ばらつきの小ささを意味する。PPVはPositive Predictive Value。

(7)   \begin{equation*} PPV = \frac{TP}{TP + FP} \end{equation*}

NPV（陰性的中率）

NPV(Negative Predictive Value)はモデルが注目事象ではないと分類して、それがあたっている率。疾病検査で陰性の場合に罹患していない率に相当する。敢えて日本語で言うなら「適正排除率」くらいか。

(8)   \begin{equation*} NPV = \frac{TN}{FN + TN} \end{equation*}

FDR（陽性誤り率？）

FDR(False Discovery Rate)はモデルが注目事象であると分類したのに、実際には非注目事象である率。英語表現の直訳なら「間違って発見する率」。検査で陽性判定だが罹患していない率に相当する。日本語の訳はないが、敢えて言うなら「過剰陽性判定率」とか「陽性失中率」くらいか。

(9)   \begin{equation*} FDR = 1 - PPV = \frac{FP}{TP + FP} \end{equation*}

FOR（陰性誤り率？）

FOR(False Omission Rate)はモデルが注目事象でないと分類したのに注目事象である率。疾病検査で陰性判定だが、実は罹患している率に相当する。英語表現の直訳なら「間違って無視してしまう率」だが、日本語なら「逸失率」くらいか。

(10)   \begin{equation*} FOR = 1 - NPV = \frac{FN}{FN + TN} \end{equation*}

指標間のトレードオフに対する疑問

一般に、Sensitivity（感度・検出率）とPrecision（適合度・陽性的中率）はトレードオフの関係にある、と述べられることが多い。これは単純な仕組みで感度を上げようとするときに、注目対象以外でも多めに陽性と判定すれば率は上がるが、その場合は陽性判定でも注目対象以外のものが多くなって適合率が下がる、ということから来ている。

ここが少しおかしい。感度を上げるにはTPを大きくしFNを小さくしなければならない。このとき適合度の側から見れば、TPが大きくなるなら適合度も上がるし、FNを小さくしたときにFPが大きくなるという相関関係がなければならない。

実際には、見落としを少なくしようとすれば、無関係なケースを陽性と判定する「濡れ衣(FP)」は増えるだろう。しかしこの「濡れ衣(FP)」は、いくら増えても感度には寄与しない。これは感度が上がっていないのに（不安なので）陽性が多めに出るようにしているに過ぎないと思われる。だとすると、このような方針は単に適合度を下げているだけで感度は向上せず、「トレードオフ」とは言えない。

その他の指標

F値

感度と適合度のトレードオフにには疑問があるが、そのバランスを保って双方向上させるというのは重要だ。このような指標がF値(F value)と呼ばれるもので、感度と適合度の調和平均として定義されている。

(11)   \begin{equation*} F = \left( \frac{1}{2} \left( \frac{1}{TPR} + \frac{1}{PPV} \right) \right) ^{-1} = \frac{2 TPR \cdot PPV}{TPR + PPV} \end{equation*}

これを4象限のパラメーターを使って書き直してみる。

(12)   \begin{align*} F = \left( \frac{1}{2} \left( \frac{TP + FN}{TP} + \frac{TP + FP}{TP} \right) \right) ^{-1} &= \frac{2 TP^2}{2TP + FN + FP} \\ &= \frac{TP}{1 + \dfrac{FN + FP}{TP}} \end{align*}

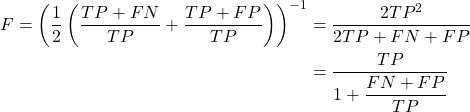
一般にF値は感度と適合率のトレードオフを想定して、双方を加味した指標とされているが、双方のバランスがとれた状態がF値を最大化するというわけでもなさそうだ。

用語について

“confusion”は、LONGMAN、Cambridgeなどの英英辞典を見ると、（不明瞭な状況、人や物事などの誤認による）混乱・混迷、（不快な状況下での）困惑というニュアンスで、confusion matrixを的確に表現できるものがない。英語サイトで「confusion matrixの語源は何か？」という問いかけがいくつか見られた。どうも心理学にその元があるようだが、その中で言及されている”classification matrix”の方が明快に思われる。実際、TP、FNなどのタームや指標の名称がかなりconfusingなことからみると、アメリカ流のジョークとも思えてしまう。

和名は「混同行列」とされているが、これも何と何を混同するのか不明瞭だ。”confusion”の的確な訳ではないので、何となくそれに近い言葉を一生懸命にあてたのかもしれない。それならいっそのこと、より的確な用語（判定行列とか）をあてればよかったのにと感じる。

 

コメントを残す

メールアドレスが公開されることはありません。 * が付いている欄は必須項目です