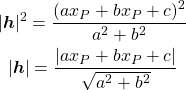点Pと直線lの距離を、媒介変数を通して愚直に求める。具体的には点Pから直線lへの垂線の足Hと点Pの距離となる。
直点をパラメーター表示し、点H(xH, yH)に対応するパラメーターをtHとする。
(1) 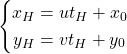
このとき、直線に沿う方向のベクトルと直線に直角なベクトルを与えられた変数で表示すると以下の通り。
(2) ![]()
これらのベクトルが直交する条件として内積をゼロとする。
(3) 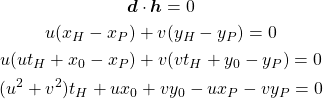
これから点Hに対する直線のパラメーターが得られる。
(4) ![]()
このパラメーターを使ってHの座標を表示すると以下の通り。
(5) 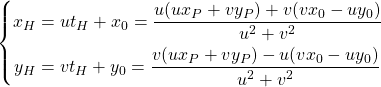
点Pと直線lの距離はベクトルhの大きさとなる。
(6) ![]()
以下、それぞれの項を計算していく。
(7) 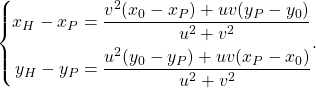
(8) 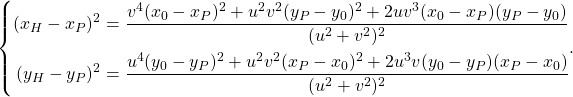
これらの結果から以下を導く。
(9) ![Rendered by QuickLaTeX.com \begin{align*} |\boldsymbol{h}|^2 &= (x_H - x_P)^2 + (y_H - y_P)^2 \\ &= \frac{ \begin{array}{l} \phantom{+}v^2(u^2+v^2)(x_0 - x_P)^2 \\ + u^2(u^2+v^2)(y_0 - y_P)^2 \\ - 2uv(u^2+v^2)(x_0 - x_P)(y_0 - y_P) \end{array} }{(u^2 + v^2)^2} \\ &= \frac{v^2(x_0 - x_P)^2 + u^2(y_0 - y_P)^2 - 2uv(x_0 - x_P)(y_0 - y_P)} {u^2 + v^2} \\ &= \frac{[v(x_0 - x_P) - u(y_0 - y_P)]^2}{u^2 + v^2} \\ &= \frac{(v x_0 - u y_0 - v x_P + v y_P)^2}{u^2 + v^2} \end{align*}](http://taustation.com/wp1/wp-content/ql-cache/quicklatex.com-0133d3c4f59238d65ef4986890dec581_l3.png)
ここで直線の一般式とパラメーター表示を比較すると
(10) 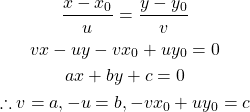
この結果を先の式に代入して以下を得る。
(11)