概要
ユークリッドの互除法(Euclidean Algorithm)は、2つの自然数の最大公約数を求める手順。
2つの自然数![]() の最大公約数(GCD: greatest common divisor)は、
の最大公約数(GCD: greatest common divisor)は、![]() と剰余
と剰余![]() の最大公約数に等しいという性質を利用。数を順次割り込んでいき、剰余がゼロとなったときの除数が最大公約数となる。
の最大公約数に等しいという性質を利用。数を順次割り込んでいき、剰余がゼロとなったときの除数が最大公約数となる。
(1) 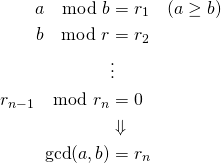
証明
以下の余りあり除算を考える。
(2) ![]()
![]() の公約数を
の公約数を![]() とすると、上式は以下のように変形され、
とすると、上式は以下のように変形され、![]() は
は![]() と
と![]() の公約数でもあることがわかる。
の公約数でもあることがわかる。
(3) ![]()
一方、![]() の公約数を
の公約数を![]() とすると、
とすると、![]() は
は![]() と
と![]() の公約数であることがわかる。
の公約数であることがわかる。
(4) ![]()
これより、![]() の公約数の集合と
の公約数の集合と![]() の公約数の集合は等しく、最大公約数も等しくなる。
の公約数の集合は等しく、最大公約数も等しくなる。
(5) ![]()
計算例
143と91の最大公約数を求める。
(6) 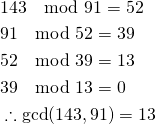
再帰関数による実装
PythonとCLispの再帰関数による実装例は以下の通り。ただし、第1引数>第2引数を前提としており、エラー処理はしていない。
Python
|
1 2 3 4 5 6 7 |
def gcd(a, b): if a % b == 0: return b else: return gcd(b, a % b) print( gcd(12, 8) ) |
CLisp
|
1 2 3 4 5 |
(defun mygcd (a b) (if (= (mod a b) 0) b (mygcd b (mod a b))) ) (print (mygcd 18 12)) |