指数分布

/ tau / コメントする

標準形

ポアソン過程の到着時間間隔や信頼性の故障発生間隔に現れる連続確率分布。単位時間当たりの到着率や発生率を\lambdaとしたとき、時刻tを確率変数とした確率密度関数と確率分布関数は以下の形になる。

(1)   \begin{equation*} f(t) = \lambda e^{- \lambda t} \end{equation*}

(2)   \begin{equation*} F(t) = 1 - e^{- \lambda t} \end{equation*}

全事象の確率が1となることの確認

(3)   \begin{equation*} \int_0^\infty \lambda e^{- \lambda t} dt = \left[ e^{-\lambda t} \right]_0^\infty = 1 \end{equation*}

平均

(4)   \begin{eqnarray*} E(t) &=& \int_0^\infty t \lambda e^{- \lambda t} dt = \int_0^\infty x e^{-x} d \frac{x}{\lambda} \\ &=& \frac{1}{\lambda} \left( \int_0^\infty e^{-x} dx - \left[ x e^{-x} \right]_0^\infty \right) = \frac{1}{\lambda} \left[ - e^{-x} - x e^{-x} \right]_0^\infty \\ &=& \frac{1}{\lambda} \end{eqnarray*}

分散

(5)   \begin{eqnarray*} V(t) &=& \int_0^\infty t^2 \lambda e^{-\lambda t} dt - \left( \frac{1}{\lambda} \right)^2 = \frac{1}{\lambda^2} \int_0^\infty x^2 e^{-x} dx - \frac{1}{\lambda^2} \\ &=& \frac{1}{\lambda^2} \left( 2 \int_0^\infty x e^{-x} dx - \left[ x^2 e^{-x} \right]_0^\infty - 1 \right) \\ &=& \frac{1}{\lambda^2} \left( \left[ -2 e^{-x} -2x e^{-x} - x^2 e^{-x} \right]_0^\infty - 1 \right) \\ &=& \frac{1}{\lambda^2} \end{eqnarray*}

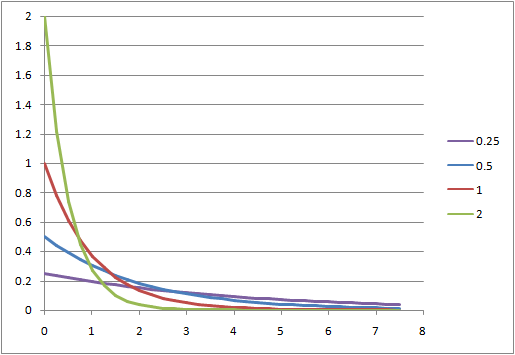
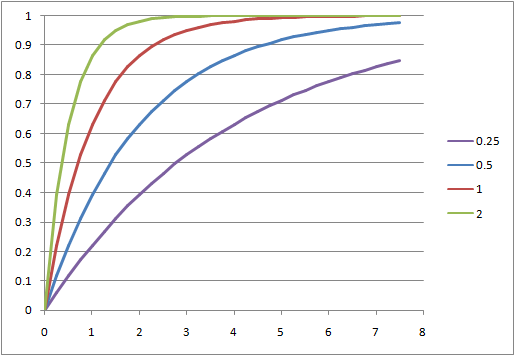
確率密度と確率分布の形状

確率密度は当然、指数関数の形状となるため、t = 0で最大値をとる単調減少関数。

このため、到着時間間隔がt以下となるような確率は、t = 0での増加率が最も大きく、その後水平に近くなっていく。

statistics-exponential-density

statistics-exponential-distribution

指数分布に関する考察

指数分布はランダムに到着する客の到着時間間隔やトランザクションの時間、信頼性における機器の故障などに現れるが、「平均発生時間間隔」があるのに何故確率密度がそれを中心とした凸型にならずに単調現象なのか、なかなかストンと胸に落ちなかった。

いろいろ考えていて、「無記憶性」の発生事象ということを考えると、次のように整理はできる。

  • 前の事象の発生と次の事象の発生に、何の因果関係もない
  • 次の瞬間、瞬間に事象が起こる率は一定
  • ということは、前の事象が起こってすぐに次の事象が起こる率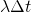\lambda \Delta tより、一定時間後に（それまで発生せず)事象が発生する確率の方が小さくなる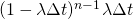(1 - \lambda \Delta t)^{n-1} \lambda \Delta t
  • ゆえに、確率密度は単調現象

 

 

 

コメントを残す

メールアドレスが公開されることはありません。 * が付いている欄は必須項目です