放物線の焦点 – TauStation

概要

放物線が、その対称軸に平行な線に対して焦点を持つことを確認する。イメージ図は以下の通り。

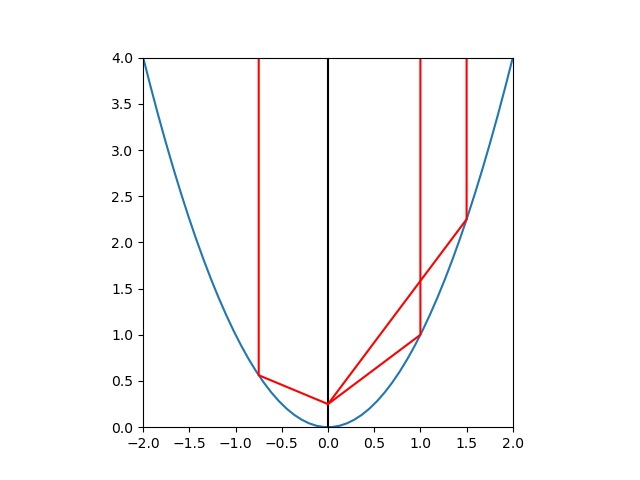
証明

下図を考える。

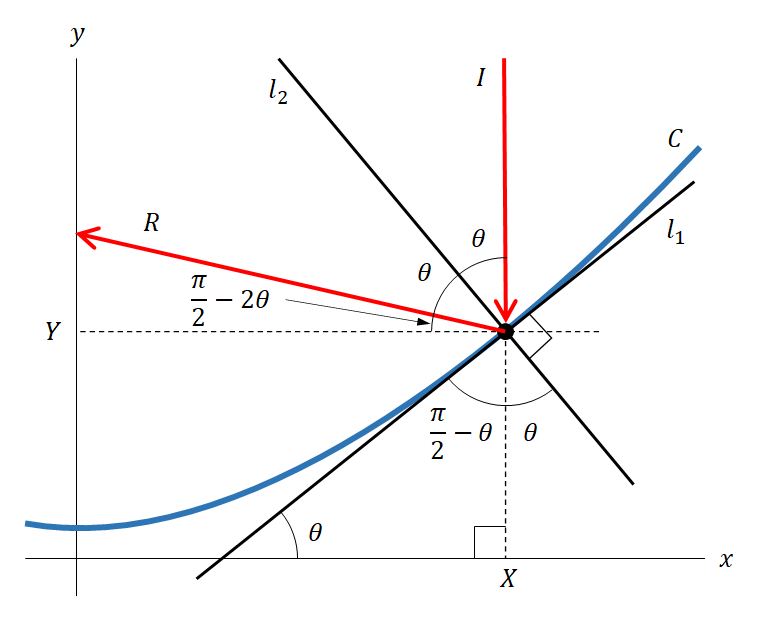
放物線Cを以下の式で定義する。

(1) $\begin{equation*} C: \: y_0(x) = a x^2 \end{equation*}$

任意の点(X, Y)における接線l₁の式は以下の様になる。

(2) $\begin{align*} l_1: \: y_1(x) &= y_1' (X) \cdot (x - X) + Y &= 2aX (x - X) + X^2 \end{align*}$

ここで、y₁‘は、図中の角θを用いて以下のように表せる。

(3) $\begin{equation*} y_1'(X) = \tan \theta \quad \left( -\frac{\pi}{2} \le \theta < \frac{\pi}{2} \right) \end{equation*}$

また、この点を通ってl₁に垂直な直線l₂の式は、この点におけるl2の微分係数をy₂‘として以下のように表せる。

(4) $\begin{equation*} l_2: \: y_2(x) = y_2' (X) \cdot (x - X) + Y \end{equation*}$

ここでy₂‘は、図中の角θを用いて以下のように導かれる。

(5) $\begin{align*} y_2'(X) &= - \tan \left( \dfrac{\pi}{2} - 2 \theta \right) \\ &= - \frac{\cos 2 \theta}{\sin 2 \theta} \\ &= - \frac{\cos^2 \theta - \sin^2 \theta}{2 \sin \theta \cos \theta} \\ &= - \frac{-1 + \tan^2 \theta}{2 \tan \theta} \end{align*}$

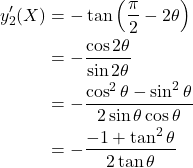
この式でθがπ/2よりも大きい場合でも、式形は変わらない。

ここで式(3)を考慮して、l₂の式は以下のように変形される。

(6) $\begin{equation*} y_2(x) = \frac{-1 + 4 a^2 X^2}{4aX} (x - X) + a X^2 \end{equation*}$

l₂がy軸と交わる点のy座標値を求める。

(7) $\begin{align*} y_2(0) &= \frac{-1 + 4 a^2 X^2}{4aX} (-X) + a X^2 \\ &= \frac{X - 4 a^2 X^3 + 4a^2 X^3}{4aX} \\ &= \frac{1}{4a} \end{align*}$

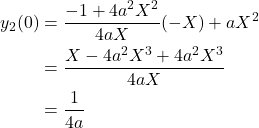
この値はXに寄らず一定なことから、y軸に平行な線が放物線で反射された線は、y軸上の1点を通る。

なお、入射線と反射線が直角になるときの入射線のx座標値は以下の通り。

(8) $\begin{align*} a x^2 = \frac{1}{4a} \quad \Leftrightarrow \quad x = \plusminus \frac{1}{2a} \end{align*}$

斜め入射について

たとえば先の図で、入射角が右側に傾いた場合を考える。

y軸の右側（xが正の側）からの入射線の放物線に対する角度は、y軸に平行な場合に対してより浅くなることから、反射方向はより下側に傾く。したがって、反射線とy軸の交点は下側に移動する。

一方y軸の左側（xが負の側）からの入射線の放物線に対する角度は、y軸に平行な場合に対してより深くなることから、反射方向はより上側に傾く。したがって、反射線とy軸の交点は上側に移動する。

少なくともy軸の両側で反射線のy軸との交点が一致しないことから、焦点は存在しない。より正確には、入射線のy軸に対する傾きをαなどと置いて上記のような計算をするとよい。

概要

証明

斜め入射について

コメントを残す コメントをキャンセル

コメントを残すコメントをキャンセル