最大公約数・最小公倍数

2019-07-13 / tau / コメントする

1 約数
2 公約数
- 2.1 0、1との公約数
- 2.2 公約数と剰余
3 最大公約数
- 3.1 0、1との最大公約数
- 3.2 最大公約数と剰余
4 倍数
5 最小公倍数
- 5.1 最大公約数と最小公倍数の積

約数

約数の定義

整数 $N$ の約数(divisor, factor)とは、Nを割り切る整数(余りが生じない除数)。

整数 $m$ が $N$ の約数であるとき、 $m|N$ と表し、ある整数 $a$ に対して $N=ma$ が成り立つことでもある。一般には自然数あるいは0以上の整数で考える。

通常は $m \ne 0$ の条件を課すが、0も含める場合は、 $N=0$ の時に限り0が約数になる。

例えば12の約数は、以下の6個。

(1) $\begin{align*}&12 \div 1 = 12 \\&12 \div 2 = 6 \\&12 \div 3 = 4 \\&12 \div 4 = 3 \\&12 \div 6 =2 \\&12 \div 12 = 1\end{align*}$

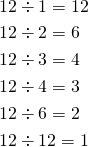
効率的な約数の求め方

$m|N$ であるとき、 $\frac Nm|N$ である。これより $m = \frac Nm$ として、 $\sqrt N$ 以下の約数 $m_i$ を求め、あとは $N/m_i$ を計算すれば、手間が半分で済む。

$N$ が平方数の場合は $\sqrt N$ も約数となり、約数の総数は奇数個、平方数でない場合は偶数異なる。

0、1の約数

0の約数は $0 = ma$ となる整数 $m$ であり、0以上の全ての整数である。

1の約数は $1 = ma$ となる整数 $m$ であり、1のみ。

1は全ての整数の約数。

素数の約数

素数の定義が「1と自身以外に約数を持たない数」なので、約数は2個。

公約数

2つの数の公約数は、それらの最大公約数の約数。

0、1との公約数

$a$ と1の公約数は1のみ。

$a$ と0の公約数は、 $a$ の約数全て(0の約数は0以上の全ての整数)。

公約数と剰余

$a \mod b = r$ のとき、 $a, b$ の公約数は $b, r$ の公約数でもある。

最大公約数

2つの数の最大公約数(greatest common divisor)を、 $\gcd(a, b)$ のように表す。

最大公約数を求める手順として、にユークリッドの互除法がある。

0、1との最大公約数

(2) $\begin{gather*}\gcd(a, 0) = a \\\gcd(a, 1) = 1\end{gather*}$

最大公約数と剰余

被除数と除数の最大公約数は、除数と剰余の最大公約数でもある。

(3) $\begin{equation*}a \mod b = r \Rightarrow \gcd(a, b) = \gcd(b, r)\end{equation*}$

倍数

倍数(multiple)とは、ある数 $a$ (整数に限らない)を整数倍した数である。

(4) $\begin{gather*}\cdots \; -3a,\; -2a,\; -a,\; 0,\; a,\; 2a,\; 3a,\; \cdots\end{gather*}$

0の倍数は0のみ
0はすべての数の倍数
すべての数は自分自身の倍数
すべての整数は1と-1の倍数

最小公倍数

最小公倍数(least common multiple)とは、2つの整数の公倍数のうち、正で最小のもの。

たとえば36と56の最小公倍数は504。

最大公約数と最小公倍数の積

2つの数 $a, b$ の積は、それらの最大公約数と最小公倍数の積に等しい。

(5) $\begin{equation*}ab = \gcd(a, b) \cdot \operatorname{lcm}(a, b)\end{equation*}$

コメントを残すコメントをキャンセル