定義
多変数の関数のグラジエント(gradient)は勾配とも呼ばれ、以下で定義される。
(1) ![]()
2変数の場合
(2) ![]()
準備~1変数関数の微分係数
微分係数の符号だけを見た場合
gradientの前に、1変数関数の微分係数についてもう一度考えてみる。
たとえば![]() は
は![]() で極値を持ち、その前後で微分係数の符号が変わる。
で極値を持ち、その前後で微分係数の符号が変わる。
(3) 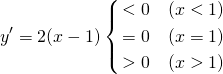
教科書的には、極値をとる点の前後で減少から増加に変わるということになる。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 |
import numpy as np import matplotlib.pyplot as plt x_min = -1 x_max = 3 x = np.linspace(x_min, x_max, 50) y = (x - 1)**2 + 1 n_points = 21 u0 = np.linspace(x_min, x_max, n_points) u = 2 * (u0 - 1) zeros = np.zeros(n_points) fig, ax = plt.subplots() ax.plot(x, y) ax.quiver(u0, zeros, zeros, u) ax.set_xlim(x_min, x_max) ax.set_ylim(x_min, x_max) ax.spines['top'].set_visible(False) ax.spines['right'].set_visible(False) ax.spines['bottom'].set_position('zero') ax.spines['left'].set_position('zero') ax.set_aspect('equal') plt.show() |
微分係数の符号を方向としてみた場合
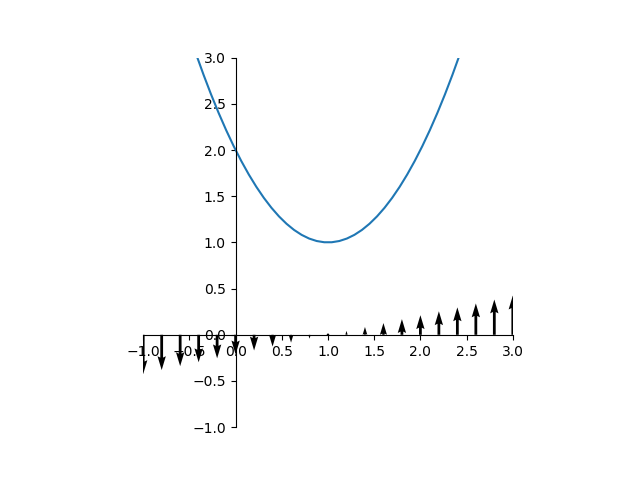
同じ微分係数の値を、それが得られる値に対して、符号を考慮して矢印で表してみる。
ただしここでは、矢印の重なりを避けるために、少しずつ縦方向にずらして描いている。
こう描いてみると分かるが、微分係数の正負が方向を表すと考えると、「微分係数は、その方向に関数がどれだけ増加の傾きを持っているか」という意味を持つことがわかる。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 |
import numpy as np import matplotlib.pyplot as plt x_min = -1 x_max = 3 x = np.linspace(x_min, x_max, 50) y = (x - 1)**2 + 1 n_points = 21 u0 = np.linspace(x_min, x_max, n_points) u = 2 * (u0 - 1) v0 = np.linspace(-0.5, 0.5, n_points) zeros = np.zeros(n_points) fig, ax = plt.subplots() ax.plot(x, y) ax.quiver(u0, v0, u, zeros) ax.set_xlim(x_min, x_max) ax.set_ylim(x_min, x_max) ax.spines['top'].set_visible(False) ax.spines['right'].set_visible(False) ax.spines['bottom'].set_position('zero') ax.spines['left'].set_position('zero') ax.set_aspect('equal') plt.show() |
微分係数の曲線上での分布
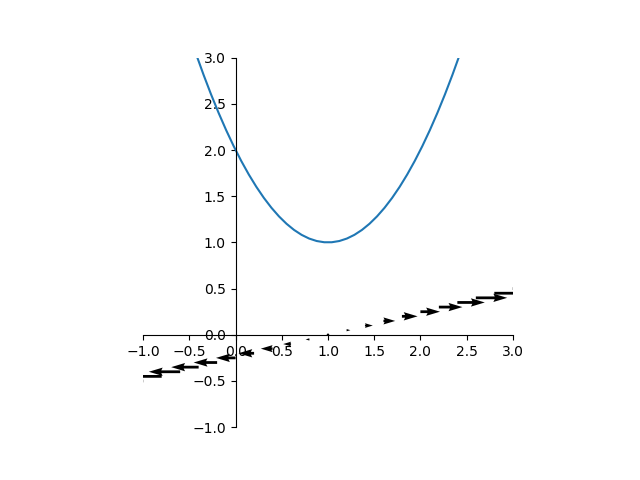
関数の曲線上で、微分係数の方向と大きさを考慮してベクトルを描いてみる。ベクトルの水平方向の成分を微分係数と同じ符号で長さ1、垂直方向の成分を微分係数の絶対値としている。
こうしてみると、微分係数は各位置での関数の増加方向とその増分を表していることがわかる。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 |
import numpy as np import matplotlib.pyplot as plt x_min = -1 x_max = 3 x = np.linspace(x_min, x_max, 50) y = (x - 1)**2 + 1 n_points = 21 u0 = np.linspace(x_min, x_max, n_points) v0 = (u0 - 1)**2 + 1 v = 2 * (u0 - 1) u = np.sign(v) v = np.abs(v) fig, ax = plt.subplots() ax.plot(x, y, color='royalblue', alpha=0.5) ax.quiver(u0, v0, u, v) ax.set_xlim(x_min, x_max) ax.set_ylim(x_min, x_max) ax.spines['top'].set_visible(False) ax.spines['right'].set_visible(False) ax.spines['bottom'].set_position('zero') ax.spines['left'].set_position('zero') ax.set_aspect('equal') plt.show() |
2変数関数のgradient
勾配ベクトルの分布
2変数の関数について、gradientの分布を描いてみる。
関数として![]() を考えると、そのgradientは
を考えると、そのgradientは![]() であり、ベクトル場は以下のようになる。
であり、ベクトル場は以下のようになる。
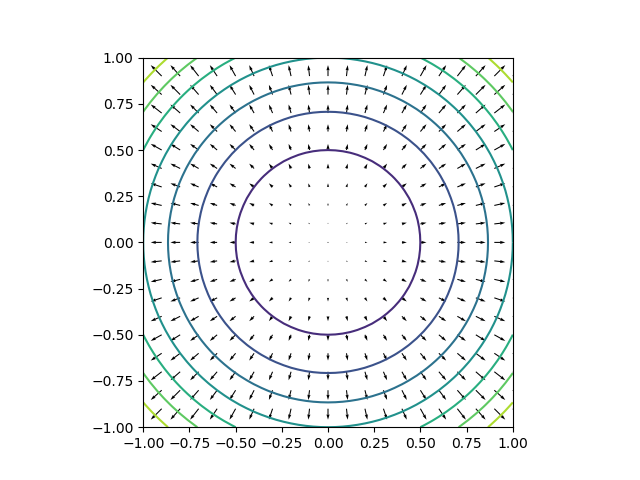
中心から外側に向かって増加しており、その傾きは外側ほど大きくなっている(ベクトルの長さが長くなり、コンター間隔は小さくなっている)。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
import numpy as np import matplotlib.pyplot as plt lim_min = -1 lim_max = 1 x = np.linspace(lim_min, lim_max, 51) y = np.linspace(lim_min, lim_max, 51) x, y = np.meshgrid(x, y) z = x * x + y* y u0 = np.linspace(lim_min, lim_max, 21) v0 = np.linspace(lim_min, lim_max, 21) u0, v0 = np.meshgrid(u0, v0) u = 2 * u0 v = 2 * v0 fig, ax = plt.subplots() ax.contour(x, y, z) ax.quiver(u0, v0, u, v) ax.set_aspect('equal') plt.show() |
勾配ベクトルの曲面上での分布
微分係数の時と同じように、曲面上にgradientoの分布を描いてみたのが以下の図。
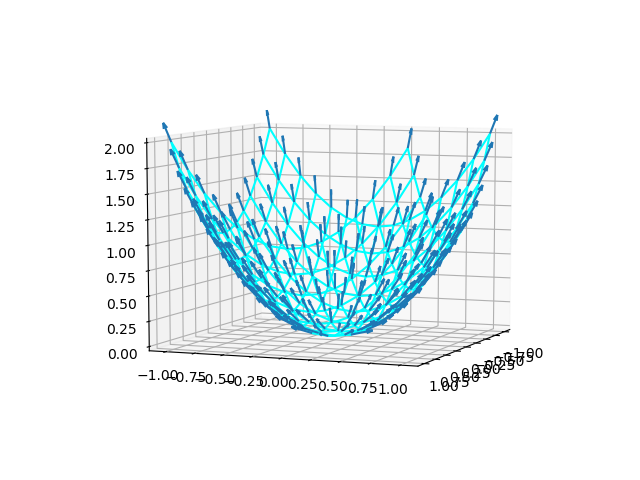
2次元の曲線の時と同じく、勾配ベクトルが曲面に沿った傾きを表していることがわかる。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 |
import numpy as np import matplotlib.pyplot as plt from mpl_toolkits.mplot3d import Axes3D lim_min = -1 lim_max = 1 n_points=15 x = np.linspace(lim_min, lim_max, n_points) y = np.linspace(lim_min, lim_max, n_points) x, y = np.meshgrid(x, y) z = x * x + y* y u0 = x v0 = y w0 = u0 * u0 + v0 * v0 u = 2 * u0 v = 2 * v0 w = np.sqrt(u * u + v * v) (u, v) = (u, v) / w fig = plt.figure() ax = fig.add_subplot(111, projection='3d') ax.plot_wireframe(x, y, z, color='cyan') ax.quiver(u0, v0, w0, u, v, w, length=0.2, normalize=True) plt.show() |
なお上記で(u, v) = (u, v) / wとしているが、![]() 方向で長さ1のベクトルを意味していて、これに対して
方向で長さ1のベクトルを意味していて、これに対して![]() をz方向の成分とすると曲面に沿ったベクトルとなる。
をz方向の成分とすると曲面に沿ったベクトルとなる。
gradientの意味
2変数の場合
(4) ![]()
gradientの方向の意味
先の微分係数の考え方から、勾配の各成分は関数の各点においてその成分方向に増加する。
したがって、gradientの方向は、関数が増加する方向を指している。
gradientの大きさの意味
(5) ![]()
ここで右辺の最初の項がgradientの絶対値だから、
(6) ![]()
![]() 、
、![]() とすると、
とすると、![]() の
の![]() 方向の変化量の大きさは
方向の変化量の大きさは![]() 以下である。
以下である。
また等号が成立するためには、
(7) 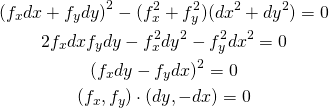
これは、![]() と
と![]() の2つのベクトルが平行であることを意味している。
の2つのベクトルが平行であることを意味している。
すなわちgradientの方向は、関数の変化量の大きさが最も大きくなる方向を指している。
gradientの意味
上記のことを併せると、gradientは以下のように最も勾配が大きな方向を意味することがわかる。
- gradientの方向は、関数がその点で最も大きく増加する方向
- gradientと逆の方向は、関数がその点で最も大きく減少する方向
n変数の場合
gradientの方向と大きさの意味は、2変数の場合と同じ。
不等式で等号が成立する場合を考える。
(8) ![]()
左辺第1項は、
(9) 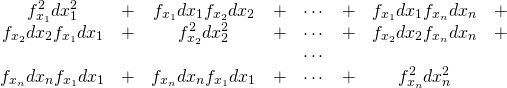
また左辺第2項は、
(10) 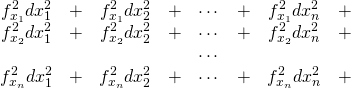
それぞれ各項が行列でいえば対角になっていることに留意しながら、(10)から(9)を差し引いて以下を得る。
(11) 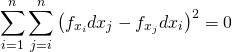
これは以下のようにも表せる。
(12) ![]()
これは以下を意味する。
(13) ![]()
すなわちn変数の場合でも、![]() と
と![]() の方向が一致するときに
の方向が一致するときに![]() の変化量が最も大きい。
の変化量が最も大きい。