逆関数による乱数の発生

問題

確率変数 $X$ が確率分布 $F(X)$ に、確率変数 $U$ が $[0, 1)$ 上の一様分布に従うとする。このとき $F^{-1} (U)$ は確率分布 $F$ に従う。

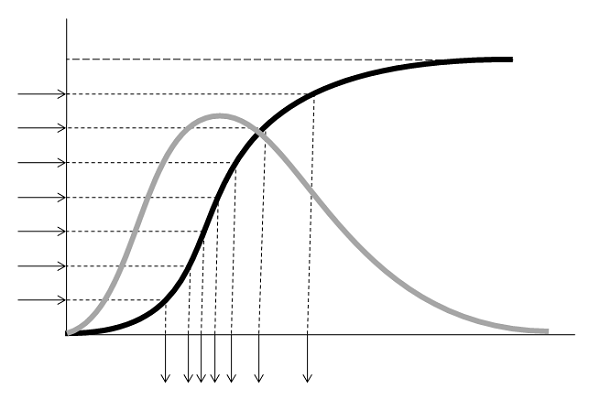
下図にもあるように、確率分布関数が立っているところ、すなわち確率密度の高いところが高くなるような乱数が生成されることになるので、直感的にわかりやすい。

stat-inverse-function-probability-number

証明

Uが一様分布に従うことを以下のように表す。

(1) $\begin{equation*} P(U \le u) = u \quad (0 \le u < 1) \end{equation*}$

確率分布関数 $F(X)$ は単調増加で、その逆関数も単調増加だから、

(2) $\begin{equation*} U \le u \Leftrightarrow F^{-1} (U) \le F^{-1} (u) \end{equation*}$

これより、

(3) $\begin{equation*} P(U \le u) = P(F^{-1}(U) \le F^{-1}(u)) = u \end{equation*}$

ここで $F^{-1}(u) = x$ とおくと、 $u = F(x)$ だから、

(4) $\begin{equation*} P(F^{-1}(U) \le x) = F(x) \end{equation*}$

すなわち確率変数 $F^{-1}$ が確率分布 $F(x)$ に従うことを意味している。

指数分布の例

指数関数の確率分布関数は以下の形をとる。

(5) $\begin{equation*} F(T \le t) = 1 - e^{- \lambda t} \end{equation*}$

これの逆関数系は以下のとおり。

(6) $\begin{equation*} F^{-1}(U) = - \frac{1}{\lambda} \ln( 1 - u) \end{equation*}$

上式の $u$ に一様乱数列を入れることで、計算結果は指数分布に従う乱数列として得られる。

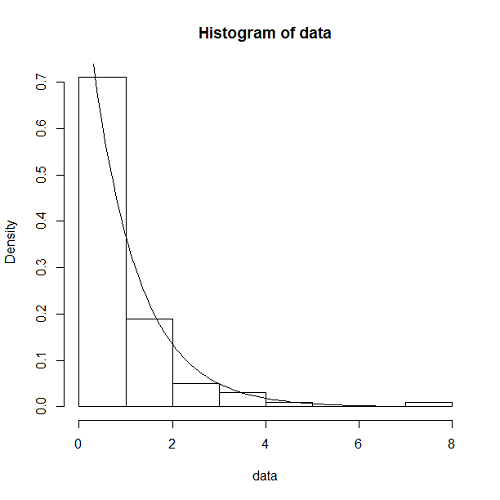
統計分析言語Rで確認したところ、一様乱数からきれいな指数乱数が得られている。

exprand <- function(dummy) return(- 1 * log(1 - runif(1)))

data <- rep(0, 100)
data <- sapply(data, exprand)

hist(data, freq=FALSE)
curve(dexp(x, rate=1), add=TRUE)

exprand <- function(dummy) return(- 1 * log(1 - runif(1)))

data <- rep(0, 100)

data <- sapply(data, exprand)

hist(data, freq=FALSE)

curve(dexp(x, rate=1), add=TRUE)

stat-inverse-function-exponential-random-number

TauStation

逆関数による乱数の発生

問題

証明

指数分布の例

コメントを残すコメントをキャンセル

問題

証明

指数分布の例

コメントを残す コメントをキャンセル

コメントを残すコメントをキャンセル