定数数列
定数数列の和は、定数の項数倍。
(1) 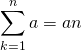
等差数列
等差数列![]() の和は、初項と末項の和に項数を乗じた数の1/2。
の和は、初項と末項の和に項数を乗じた数の1/2。
(2) 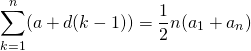
特に、
(3) 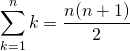
証明1
等差数列の![]() 項目までの和を
項目までの和を![]() とすると、
とすると、
(4) 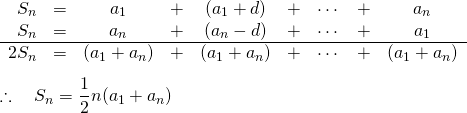
証明2
式(3)を使って、
(5) 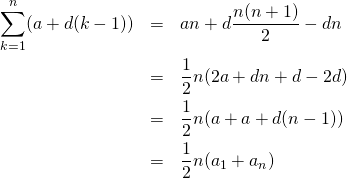
等比数列
等比数列![]() の和は以下の通り。
の和は以下の通り。
(6) 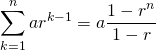
特に、
(7) 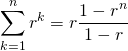
証明
等差数列の![]() 項目までの和を
項目までの和を![]() とすると、
とすると、
(8) 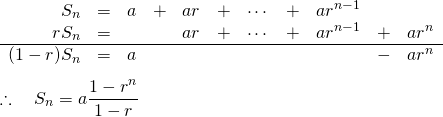
等比・等差の複合数列
等差部分と等比部分の両方を含んだ数列の部分和。
(9) 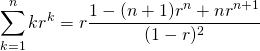
証明1
一般的な部分和の差を用いる方法。
(10) 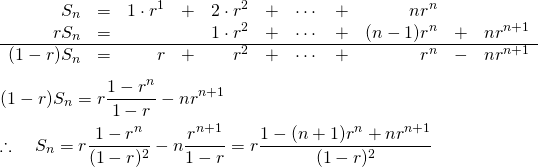
証明2
微分を用いる方法。等比数列の公式、
(11) 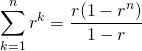
の両辺を![]() で微分すると、
で微分すると、
(12) 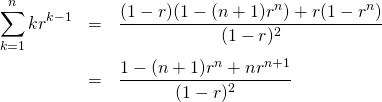
両辺を![]() 倍して同じ式を得る。
倍して同じ式を得る。
べき乗の数列
∑k2
(13) 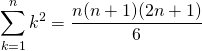
証明
以下の式から出発する。
(14) 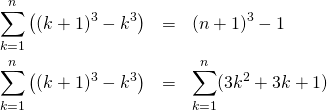
これより、
(15) 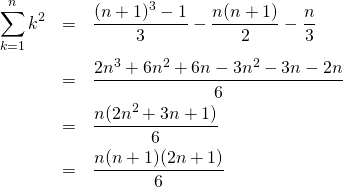
∑k3
(16) 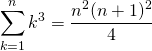
証明
上記と同じように、
(17) 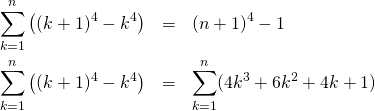
これより、
(18) 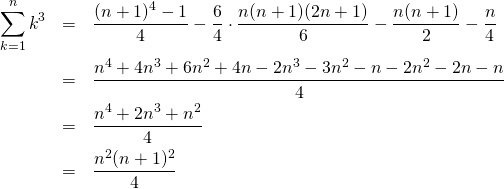
階差数列
数列![]() の階差数列が扱いやすい数列の場合。
の階差数列が扱いやすい数列の場合。
(19) ![]()
![]() の各項は、
の各項は、![]() ~
~![]() の和をとることで以下のように得られる。
の和をとることで以下のように得られる。
(20) 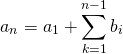
【例】
![]() の階差数列が
の階差数列が![]() で
で![]() のときの数列
のときの数列![]() は以下のようになる
は以下のようになる
![]()
この数列の一般項は、
(21) 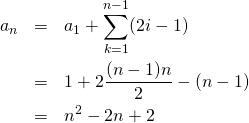
上式は![]() の時も初期条件
の時も初期条件![]() を満足する。
を満足する。