過学習～多項式回帰の場合

1 概要
2 データ数が少ない場合
3 異常値がある場合
4 データ数を多くした場合

概要

過学習(over fitting)の例として、多項式の係数を線形回帰で予測した場合の挙動をまとめてみた。

複数の点(x_i, y_i)に対して、以下の線形式の項数を変化させて、Pythonのパッケージ、scikit-learnにあるLinearRegressionでフィッティングさせてみる。

(1) $\begin{equation*} \hat{y} = w_0 + \sum_{j=1}\m w_j x^j \end{equation*}$

データ数が少ない場合

以下の例は、[-3, 1]の間で等間隔な4つの値を発生させ、(x, e^x)となる4つの点を準備、これらのデータセットに対して、多項式の項数（すなわちxの次数）を1～6まで変化させてフィッティングした結果。たとえばn_terms=3の場合は $y = w_0 + w_1 x + w_2 x^2 + w_3 x^3$ の4つの係数を決定することになる。

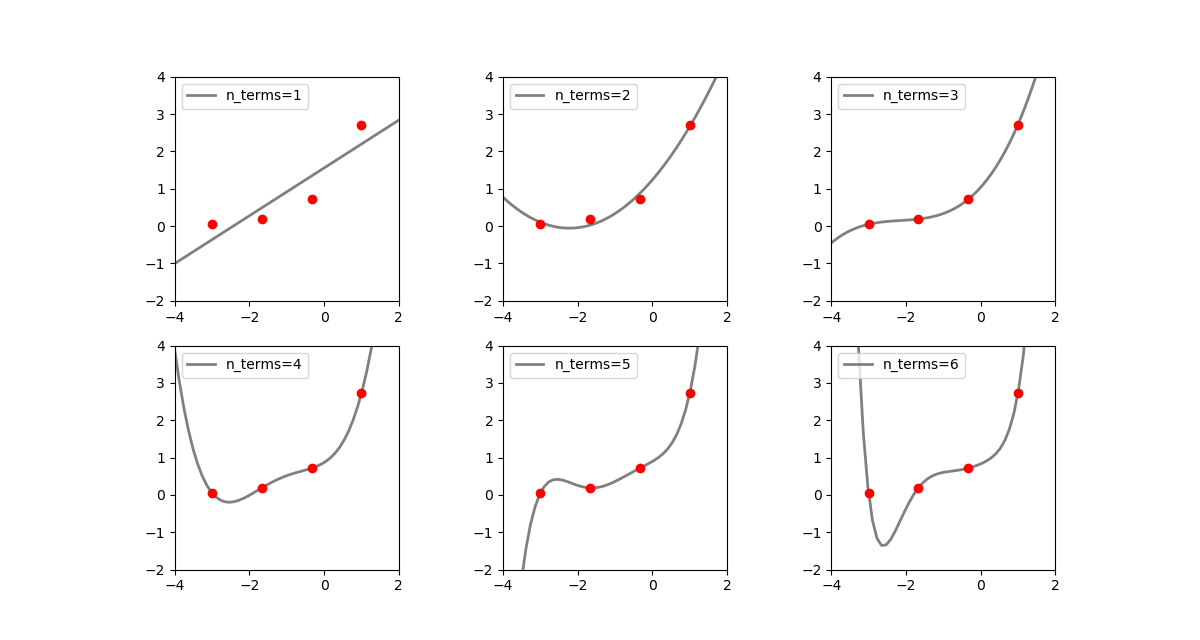
n_terms=1の場合は単純な線形関数で、データセットの曲線関係を表しているとは言えない。
n_terms=2になるとかなり各点にフィットしているが、x < −1の範囲で本来の関数の値と離れていく。
n_terms=3はデータ数より項数（特徴量の数）が1つ少ない。各点にほぼぴったり合っていて、最も「それらしい」（ただしデータセットの外側の範囲でも合っているとは限らない／指数関数に対してxの有限の多項式ではどこかで乖離していく）
n_terms=4はデータ数と項数（特徴量の数）が等しい。予測曲線がすべての点を通っているが、無理矢理合わせている感があり、データセットの左側で関数形が跳ね上がっている。
n_terms=5はデータ数より特徴量数の方が多くなる。予測曲線は全ての点を通っているが、1番目の点と2番目の点の間で若干曲線が歪んでいる
n_terms=6になると歪が大きくなる

上記の実行コードは以下の通り。

7～8行目は、切片・係数のセットとxの値を与えて多項式の値を計算する関数。
19行目でn_data=4個のxの値を発生させ、20行目で指数関数の値を計算している。後のために乱数でばらつかせる準備をしているが、ここではばらつかせていない
23～24行目でxⁿの特徴量を生成している
35行目で線形回帰モデルのフィッティングを行っている。n_termsで指定した項数（＝次数）までをフィッティングに使っている。
36行目で、フィッティングの結果予測された切片と係数を使って、予測曲線の値を計算している。

import numpy as np
import random as rnd
import pandas as pd
from sklearn.linear_model import LinearRegression
import matplotlib.pyplot as plt

def poly(intercept, coef, x):
    return intercept + sum([w * x**(n + 1) for n, w in enumerate(coef)])

rnd.seed(0)
xmin, xmax = -3, 1
xlim_min, xlim_max = -4, 2
ylim_min, ylim_max = -2, 4

n_data = 4
n_features = 20
n_terms_list = [1, 2, 3, 4, 5, 6]

x = np.linspace(xmin, xmax, n_data)
y = np.exp(x) + [rnd.uniform(-0.0, 0.0) for n in range(n_data)]

df = pd.DataFrame(y, columns=['y'])
for n in range(n_features):
    df["x^{}".format(n+1)] = x**(n+1)
print(df)

fig, axs = plt.subplots(2, 3, figsize=(12, 6.4))
axs_1d = axs.reshape(1, -1)[0]

linreg = LinearRegression()

x_graph = np.linspace(xlim_min, xlim_max)

for ax, n_terms in zip(axs_1d, n_terms_list):
    linreg.fit(df.iloc[:, 1:n_terms+1], df['y'])
    y_linreg = poly(linreg.intercept_, linreg.coef_, x_graph)
    ax.scatter(df['x^1'], df['y'], c='r', zorder=10)
    ax.plot(x_graph, y_linreg, c='gray', linewidth=2,
        label="n_terms={}".format(n_terms))

    ax.set_xlim(xlim_min, xlim_max)
    ax.set_ylim(ylim_min, ylim_max)
    ax.set_aspect('equal')
    ax.legend(loc='upper left')

plt.show()

import numpy as np

import random as rnd

import pandas as pd

from sklearn.linear_model import LinearRegression

import matplotlib.pyplot as plt

def poly(intercept, coef, x):

return intercept + sum([w * x**(n + 1) for n, w in enumerate(coef)])

rnd.seed(0)

xmin, xmax = -3, 1

xlim_min, xlim_max = -4, 2

ylim_min, ylim_max = -2, 4

n_data = 4

n_features = 20

n_terms_list = [1, 2, 3, 4, 5, 6]

x = np.linspace(xmin, xmax, n_data)

y = np.exp(x) + [rnd.uniform(-0.0, 0.0) for n in range(n_data)]

df = pd.DataFrame(y, columns=['y'])

for n in range(n_features):

df["x^{}".format(n+1)] = x**(n+1)

print(df)

fig, axs = plt.subplots(2, 3, figsize=(12, 6.4))

axs_1d = axs.reshape(1, -1)[0]

linreg = LinearRegression()

x_graph = np.linspace(xlim_min, xlim_max)

for ax, n_terms in zip(axs_1d, n_terms_list):

linreg.fit(df.iloc[:, 1:n_terms+1], df['y'])

y_linreg = poly(linreg.intercept_, linreg.coef_, x_graph)

ax.scatter(df['x^1'], df['y'], c='r', zorder=10)

ax.plot(x_graph, y_linreg, c='gray', linewidth=2,

label="n_terms={}".format(n_terms))

ax.set_xlim(xlim_min, xlim_max)

ax.set_ylim(ylim_min, ylim_max)

ax.set_aspect('equal')

ax.legend(loc='upper left')

plt.show()

異常値がある場合

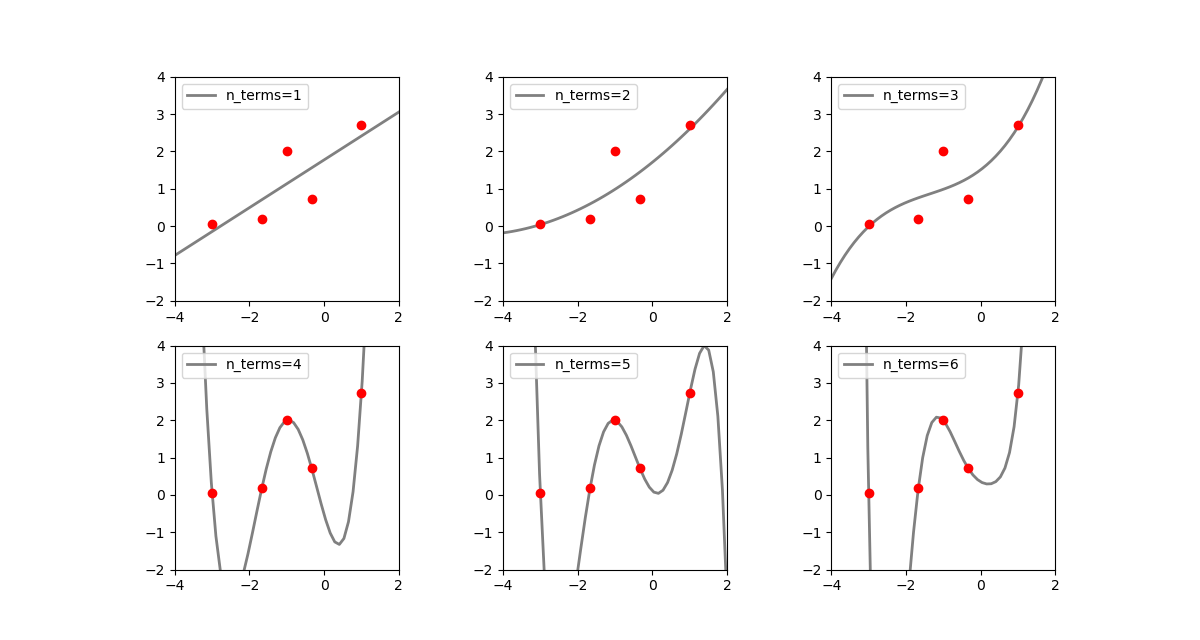
上記の整然とした指数関数のデータに1つだけ飛び離れた異常値を入れてみる。

x = np.linspace(xmin, xmax, n_data)
y = np.exp(x) + [rnd.uniform(-0.0, 0.0) for n in range(n_data)]
x = np.append(x, -1)
y = np.append(y, 2)

x = np.linspace(xmin, xmax, n_data)

y = np.exp(x) + [rnd.uniform(-0.0, 0.0) for n in range(n_data)]

x = np.append(x, -1)

y = np.append(y, 2)

先の例に比べて不安定性＝曲線の振動の度合いが大きくなっている。

データ数を多くした場合

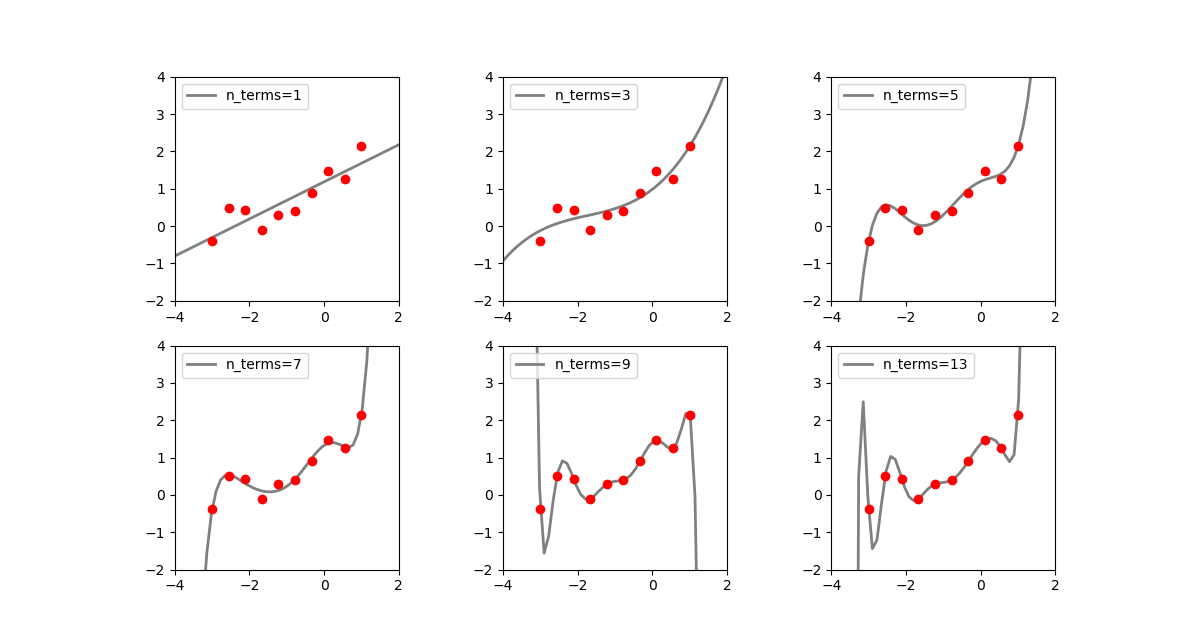
点の数を10個とし、乱数で擾乱を与えてみる（乱数系列も変えている）。

rnd.seed(1)

.....

n_data = 10
n_features = 20
n_terms_list = [1, 3, 5, 7, 9, 13]

x = np.linspace(xmin, xmax, n_data)
y = np.exp(x) + [rnd.uniform(-0.6, 0.6) for n in range(n_data)]

rnd.seed(1)

.....

n_data = 10

n_features = 20

n_terms_list = [1, 3, 5, 7, 9, 13]

x = np.linspace(xmin, xmax, n_data)

y = np.exp(x) + [rnd.uniform(-0.6, 0.6) for n in range(n_data)]

n_terms=5あたりから、全ての点に何とかフィットさせようと曲線が揺れ始め、特徴量数がデータ数と同じ値となる前後から振動が大きくなっている。

TauStation

過学習～多項式回帰の場合

概要

データ数が少ない場合

異常値がある場合

データ数を多くした場合

コメントを残すコメントをキャンセル

概要

データ数が少ない場合

異常値がある場合

データ数を多くした場合

コメントを残す コメントをキャンセル

コメントを残すコメントをキャンセル