単位時間当たりの到着率![]() のポアソン過程において、
のポアソン過程において、![]() 時間の間に
時間の間に![]() 回の到着が発生する確率を考える。
回の到着が発生する確率を考える。
![]() を
を![]() 等分し、
等分し、![]() とする。この間に
とする。この間に![]() 回の到着が発生し、
回の到着が発生し、![]() 回は到着が発生しないとすると、その確率は次の二項分布で表される。
回は到着が発生しないとすると、その確率は次の二項分布で表される。
(1) ![]()
この式を、以下のように展開しておく。
(2) 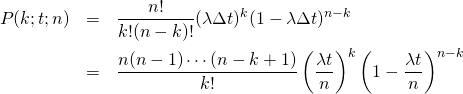
ここで![]() の極限を考える。まず前2項については、
の極限を考える。まず前2項については、
(3) 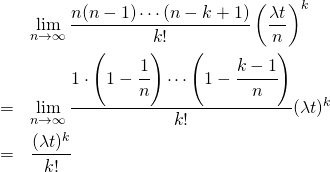
また3項目については![]() とおいて、
とおいて、
(4) ![Rendered by QuickLaTeX.com \begin{equation*} \lim_{r \to \infty} \left( 1 + \frac{1}{r} \right)^{- r \lambda t - k} = \lim_{r \to \infty}\left[ \left(1 + \frac{1}{r} \right)^{- r \lambda t} \left( 1 + \frac{1}{r} \right)^{-k} \right] = e^{- \lambda t} \end{equation*}](http://taustation.com/wp1/wp-content/ql-cache/quicklatex.com-49d81edd3149a98b9a6ef1f587e3e521_l3.png)
通常、Poisson分布の表現は上式において![]() として表現されるが、この場合の
として表現されるが、この場合の![]() は観測時間内の平均到着数として考える。ここでは、単位時間あたりの到着率
は観測時間内の平均到着数として考える。ここでは、単位時間あたりの到着率![]() と観測時間
と観測時間![]() を明確にするため
を明確にするため![]() と表現した。
と表現した。
以上から、到着率![]() のポアソン過程において、観測時間
のポアソン過程において、観測時間![]() の間に
の間に![]() 回の到着が発生する確率は以下のPoisson分布で与えられる。
回の到着が発生する確率は以下のPoisson分布で与えられる。
(5) ![]()