時刻制御による分析
時刻制御(time driven)の考え方では、時刻を変化させながら、その都度到着イベントが発生するかどうかを確率的に計算し、到着パターンのデータを生成していく。計算にはR言語を使う。
時刻制御の考え方の概要やその他の考え方についてはRによるポアソン過程のシミュレーションを参照。
到着イベントの時系列
上のRのコードでは、到着率λに短い時間間隔dtを掛けた確率でその時間間隔t ~ t + dtの間に到着イベントを発生させている。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
lambda <- 1 / 10 t.obs <- 1000 dt = 0.1 nstep = floor(t.obs / dt) rank.width <- 100 data <- c() t <- 0 for (i in 1:nstep) { t <- dt * i if (runif(1) < lambda * dt) data <- c(data, t) } hist(data) |
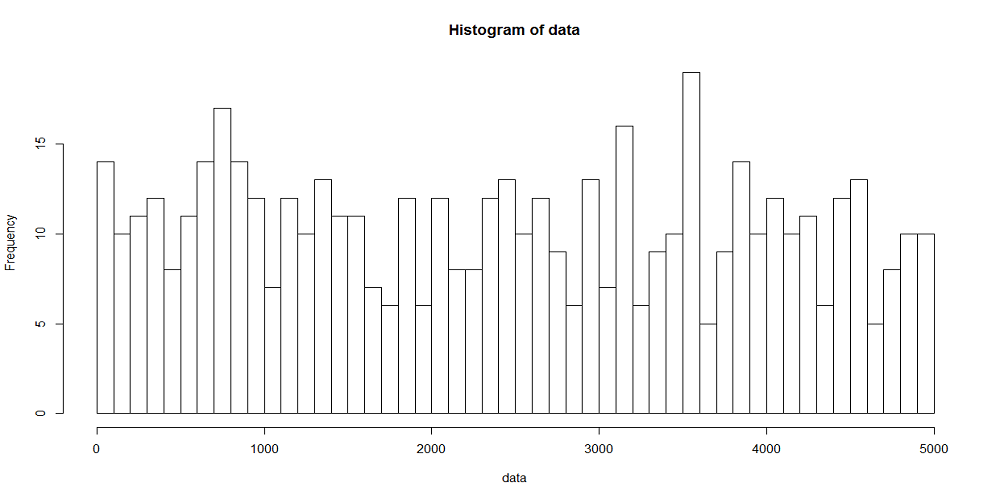
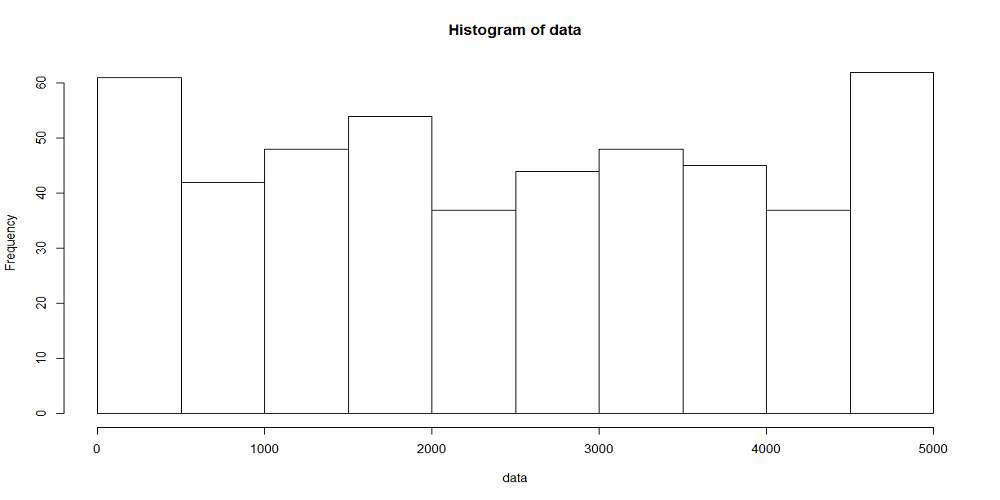
以下に観測時間が5000秒のときの、階級幅が100秒、500秒に対する到着数の時系列分布をヒストグラムを示す。階級当たりのデータ数が多いほど平滑化される傾向は、一様分布によって到着イベントを発生させたときと同じ。
到着時間間隔の分布
一様乱数のときと同じく、到着時間間隔の分布をチェックする。期待した通り、指数分布の確率密度関数とよく合っている。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
generate <- function(t.obs, lambda, dt) { data <- c() t <- 0 for (i in 1:floor(t.obs / dt)) { t <- dt * i if (runif(1) < lambda * dt) data <- c(data, t) } return(data) } lambda <- 1 / 10 t.obs <- 1000 dt = 0.1 data = generate(t.obs, lambda, dt) interval <- data[-1] - data[-length(data)] hist(interval, freq=FALSE) curve(dexp(x, rate=lambda), add=TRUE) |

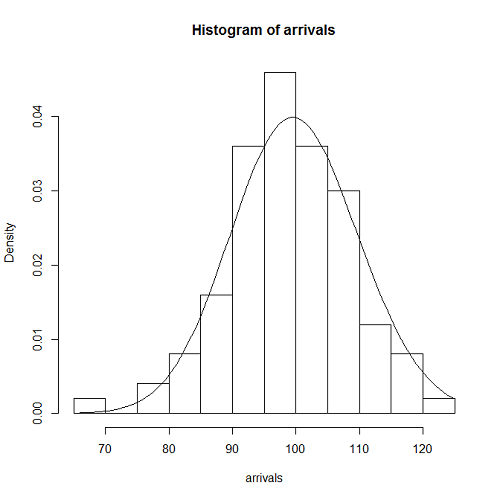
到着数の分布
到着数の分布についても、一様分布のときと同じように調べると、Poisson分布の形状とよく合っている。
なおtime drivenの場合は、細かい時間間隔について到着判定をしているのでループ回数が多くなり、計算時間が少しかかる。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
generate <- function(t.obs, lambda, dt) { data <- c() t <- 0 for (i in 1:floor(t.obs / dt)) { t <- dt * i if (runif(1) < lambda * dt) data <- c(data, t) } return(data) } lambda <- 1 / 10 t.obs <- 1000 dt = 0.1 n.loop <- 100 arrivals <- rep(0, n.loop) for (n in 1:n.loop) { data = generate(t.obs, lambda, dt) arrivals[n] <- length(data) } hist(arrivals, freq=FALSE) curve((lambda*t.obs)^x/factorial(x)*exp(-lambda*t.obs), add=TRUE) |