定義
平均の定義には標本平均と確率変数の平均があって、それぞれ定義が異なるので、ここで整理する。
標本平均に対しては算術平均、幾何平均、調和平均などの定義があるが、ここでは算術平均を対象とする。
標本平均
標本平均は、標本データの値を足し合わせてその個数で割った値。
標本の値が![]() のとき、標本平均
のとき、標本平均![]() は標本値の算術平均で定義される。
は標本値の算術平均で定義される。
(1) 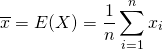
確率変数の平均
確率変数の平均は、離散型の場合と連続型の場合それぞれで定義される。
離散型の確率変数![]() が
が![]() の値を取り、それぞれの値をとる確率を
の値を取り、それぞれの値をとる確率を![]() と表すと、
と表すと、![]() の母平均
の母平均![]() は確率変数とその確率変数の発生確率の積の総和で定義される。
は確率変数とその確率変数の発生確率の積の総和で定義される。
(2) 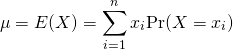
連続型の確率変数の平均は、確率密度関数を![]() とすると、
とすると、![]() の母平均
の母平均![]() は、確率変数とその値に対する確率密度の積の全定義域における積分で定義される。
は、確率変数とその値に対する確率密度の積の全定義域における積分で定義される。
(3) ![]()
平均(期待値)の性質
平均(期待値)には以下の性質がある。これらは、母集団の確率分布に関係なく常に成り立つ。
(4) ![]()
(5) ![]()
(6) ![]()
定数加算
標本値、確率変数に定数を加えた場合の平均は、元の平均に定数を加えた値に等しい。
![]()
証明:標本平均
(7) 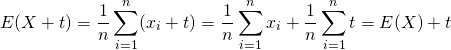
証明:離散型確率変数
(8) 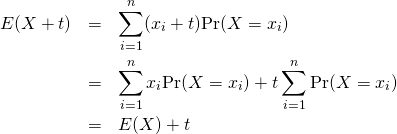
証明:連続型確率変数
(9) 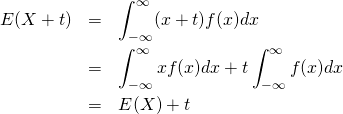
定数倍
標本値、確率変数を定数倍した場合の平均は、元の平均の定数倍に等しい。
![]()
証明:標本平均
(10) 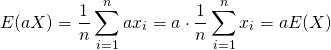
証明:離散型確率変数
(11) 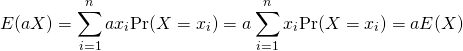
証明:連続型確率変数
(12) ![]()
和の平均
複数の標本値(データセット)、確率変数を加えた場合の平均は、それぞれの平均の和に等しい
![]()
証明:標本平均
(13) 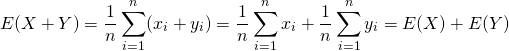
証明:離散型確率変数
確率変数![]() が
が![]() 、
、![]() が
が![]() であり、
であり、![]() 、
、![]() はそれぞれの確率分布に従うとする。また、
はそれぞれの確率分布に従うとする。また、![]() と
と![]() の同時生起確率を
の同時生起確率を![]() と表す。
と表す。
このとき、確率変数![]() の平均は以下のように計算される。
の平均は以下のように計算される。
(14) 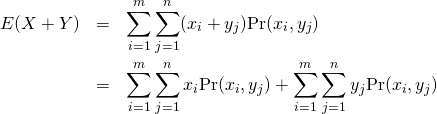
上式の第1項についてみると、![]() の値に対してすべての
の値に対してすべての![]() のとりうる値を考慮していることから、
のとりうる値を考慮していることから、![]() とそれに対する生起確率
とそれに対する生起確率![]() となり、第1項は
となり、第1項は![]() の平均となる。
の平均となる。
(15) 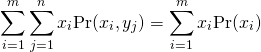
第2項も同様に![]() の平均なので、以下が成り立つ。
の平均なので、以下が成り立つ。
![]()
証明:連続型確率変数
確率変数![]() に対する同時生起確率密度を
に対する同時生起確率密度を![]() とすると、
とすると、
(16) 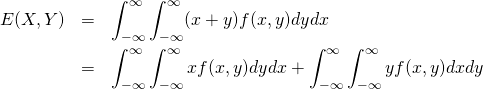
離散型と同様の考え方により、上式の第1項、第2項はそれぞれ![]() の平均となり、次式が成り立つ。
の平均となり、次式が成り立つ。
![]()