待ち行列 – TauStation

考え方

M/M1待ち行列のシミュレーションを、イベント制御(event driven)で行う。M/M/1待ち行列の解析的アプローチはこちら。言語はRを使う。なお時刻制御によるケースはこちら。

計算手順のブロックは次の3つ。

全てのトランザクションの到着時刻を指数分布に従って発生させる
時刻0から指数分布に従ってサービス時間を1つずつ発生させる
1. 待ち状態のトランザクションがあればすぐに次のサービスを開始
2. 待ち状態のトランザクションがなければ、次のトランザクション到着時にサービス開始
待ち行列長の推移を集計し、結果を表示する

定数定義

##########
# 定数設定
##########

# トランザクションの到着率とサービス率
lambda <- 1/10
mu <- 1/5

# 生成するトランザクションの数
# このうち真ん中のの1/3だけ最終的に使う
num.trs <- 3000

##########

# 定数設定

##########

# トランザクションの到着率とサービス率

lambda <- 1/10

mu <- 1/5

# 生成するトランザクションの数

# このうち真ん中のの1/3だけ最終的に使う

num.trs <- 3000

トランザクションの到着時刻の発生

到着時間間隔を乱数で発生させてトランザクションの到着時刻を発生させる。手順についてはイベント制御によるポアソン過程のシミュレーションを参照。

#################################
# 第1ステップ
# トランザクションの時系列データを生成
#################################

# trs:トランザクション
# svc:サービス
# arv:到着
# sta:開始
# end:終了
# wat:待ち時間
trs.arv <- numeric(num.trs)
trs.svc.sta <- numeric(num.trs)
trs.svc.end <- numeric(num.trs)
svc.sta <- c(0)
svc.end <- numeric(0)
trs.wat.svc.sta <- numeric(num.trs)
trs.wat.svc.end <- numeric(num.trs)

# 全てのトランザクションの到着時刻を指数分布の間隔で生成
exp.rand <- rexp(num.trs, rate=lambda)
for (i in 2:num.trs)
  trs.arv[i] <- trs.arv[i-1] + exp.rand[i-1]

#################################

# 第1ステップ

# トランザクションの時系列データを生成

#################################

# trs:トランザクション

# svc:サービス

# arv:到着

# sta:開始

# end:終了

# wat:待ち時間

trs.arv <- numeric(num.trs)

trs.svc.sta <- numeric(num.trs)

trs.svc.end <- numeric(num.trs)

svc.sta <- c(0)

svc.end <- numeric(0)

trs.wat.svc.sta <- numeric(num.trs)

trs.wat.svc.end <- numeric(num.trs)

# 全てのトランザクションの到着時刻を指数分布の間隔で生成

exp.rand <- rexp(num.trs, rate=lambda)

for (i in 2:num.trs)

trs.arv[i] <- trs.arv[i-1] + exp.rand[i-1]

サービス時間の計算

下図に考え方を示す。

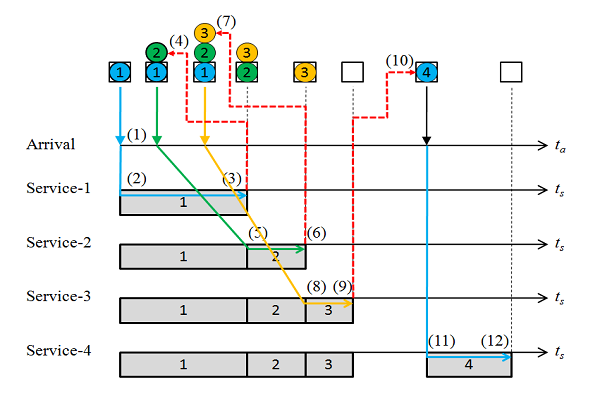
queue-mm1-event-driven-fig1

時刻0でトランザクション1到着
時刻0でサービス1開始
指数乱数でサービス1の終了時刻を計算
終了時刻より前に次のトランザクション2が到着している
すぐにトランザクション2に対してサービス2を開始
サービス2の終了時刻を指数乱数で計算
終了時刻より前に次のトランザクション3が到着している
すぐにトランザクション3に対してサービス3を開始
サービス3の終了時刻を指数乱数で計算
次のトランザクション4の到着は終了時刻より後
トランザクション4の到着と同時にサービス4を開始する
サービス4の終了時刻を指数乱数で計算

#########################
# 第2ステップ
# サービスの開始・終了時刻の計算
#########################

# 時刻0でトランザクション到着、サービス開始
it <- 1
is <- 1

# 全てのトランザクションに対して実行
while (it <= num.trs) {
  # 現在のサービスの終了時刻を指数分布で計算し、トランザクションを1つ解放
  svc.end[is] <- svc.sta[is] + rexp(1, rate=mu)
  trs.svc.end[it] <- svc.end[is]
  trs.wat.svc.end[it] <- trs.svc.end[it] - trs.arv[it]
  # 最後の客なら計算だけして終わり
  if (it == num.trs) break

  # 次のサービス開始
  is <- is + 1
  it <- it + 1

  if (trs.arv[it] < svc.end[is - 1]) {
  # 待ち行列に客がいる場合、すぐに先頭の客のサービスを開始
    trs.svc.sta[it] <- svc.sta[is] <- svc.end[is - 1]
  } else {
  # 待ち行列に客がいない場合、最初に到着する客に対してサービスを開始
    trs.svc.sta[it] <- svc.sta[is] <- trs.arv[it]
  }
  trs.wat.svc.sta[it] <- trs.svc.sta[it] - trs.arv[it]
}

# トランザクションに関するデータの集計
trs.time.sequence <- data.frame(
  arrive = trs.arv,
  start = trs.svc.sta,
  end = trs.svc.end,
  trs.time = trs.wat.svc.end,
  queue.time = trs.wat.svc.sta
)

#########################

# 第2ステップ

# サービスの開始・終了時刻の計算

#########################

# 時刻0でトランザクション到着、サービス開始

it <- 1

is <- 1

# 全てのトランザクションに対して実行

while (it <= num.trs) {

# 現在のサービスの終了時刻を指数分布で計算し、トランザクションを1つ解放

svc.end[is] <- svc.sta[is] + rexp(1, rate=mu)

trs.svc.end[it] <- svc.end[is]

trs.wat.svc.end[it] <- trs.svc.end[it] - trs.arv[it]

# 最後の客なら計算だけして終わり

if (it == num.trs) break

# 次のサービス開始

is <- is + 1

it <- it + 1

if (trs.arv[it] < svc.end[is - 1]) {

# 待ち行列に客がいる場合、すぐに先頭の客のサービスを開始

trs.svc.sta[it] <- svc.sta[is] <- svc.end[is - 1]

} else {

# 待ち行列に客がいない場合、最初に到着する客に対してサービスを開始

trs.svc.sta[it] <- svc.sta[is] <- trs.arv[it]

}

trs.wat.svc.sta[it] <- trs.svc.sta[it] - trs.arv[it]

}

# トランザクションに関するデータの集計

trs.time.sequence <- data.frame(

arrive = trs.arv,

start = trs.svc.sta,

end = trs.svc.end,

trs.time = trs.wat.svc.end,

queue.time = trs.wat.svc.sta

)

待ち行列長の推移の集計

以下の手順によっている。

トランザクションの到着時とサービス終了時の時刻を取り出し、時刻と増減値をデータフレームにまとめる
時刻順にソート
待ち行列長の推移を計算する

ここで、トランザクション数と待ち行列長には、到着したトランザクション自身はカウントしていない(長さ0も考慮するため)。

####################################
# 第3ステップ
# 時系列データから待ち行列変化時系列を生成
####################################

# トランザクション数の増減が発生した時刻を記録するベクトル
evt.time <- c(trs.time.sequence$arrive, trs.time.sequence$end)
# システムのトランザクション数の増減を記録するベクトル
# arriveで+1、endで-1
trs.change <-c(rep(+1, num.trs), rep(-1, num.trs))
# サービス中のトランザクションを除いた待ち行列長を記録するベクトル
queue <- rep(0, num.trs*2)

# トランザクション数と待ち行列をデータフレーム化
system.trs <- data.frame(
  time = evt.time,
  change = trs.change,
  transactions = rep(0, 2*num.trs))
system.trs <- system.trs[order(system.trs$time),]
rownames(system.trs) <- 1:nrow(system.trs)

# 時刻0での待ち行列から、その後の待ち行列長を計算
# 注意点：トランザクション数や待ち行列長に自分自身は数えない
system.trs$transactions[1] <- 0
queue[1] <- 0
for (i in 2:nrow(system.trs)) {
  n <- system.trs$transactions[i] <-
    system.trs$transactions[i-1] + system.trs$change[i]
  if (n <= 1) queue[i] <- 0 else queue[i] <- n - 1
}
system.trs <- cbind(system.trs, queue)

# トランザクション到着時のトランザクション数と待ち行列長を抜き出し
# 総括データフレームに集約
temp.frame <- system.trs[system.trs$change==1,]
trs.time.sequence <- cbind(trs.time.sequence, transactions=temp.frame$transactions)
trs.time.sequence <- cbind(trs.time.sequence, queue=temp.frame$queue)

####################################

# 第3ステップ

# 時系列データから待ち行列変化時系列を生成

####################################

# トランザクション数の増減が発生した時刻を記録するベクトル

evt.time <- c(trs.time.sequence$arrive, trs.time.sequence$end)

# システムのトランザクション数の増減を記録するベクトル

# arriveで+1、endで-1

trs.change <-c(rep(+1, num.trs), rep(-1, num.trs))

# サービス中のトランザクションを除いた待ち行列長を記録するベクトル

queue <- rep(0, num.trs*2)

# トランザクション数と待ち行列をデータフレーム化

system.trs <- data.frame(

time = evt.time,

change = trs.change,

transactions = rep(0, 2*num.trs))

system.trs <- system.trs[order(system.trs$time),]

rownames(system.trs) <- 1:nrow(system.trs)

# 時刻0での待ち行列から、その後の待ち行列長を計算

# 注意点：トランザクション数や待ち行列長に自分自身は数えない

system.trs$transactions[1] <- 0

queue[1] <- 0

for (i in 2:nrow(system.trs)) {

n <- system.trs$transactions[i] <-

system.trs$transactions[i-1] + system.trs$change[i]

if (n <= 1) queue[i] <- 0 else queue[i] <- n - 1

}

system.trs <- cbind(system.trs, queue)

# トランザクション到着時のトランザクション数と待ち行列長を抜き出し

# 総括データフレームに集約

temp.frame <- system.trs[system.trs$change==1,]

trs.time.sequence <- cbind(trs.time.sequence, transactions=temp.frame$transactions)

trs.time.sequence <- cbind(trs.time.sequence, queue=temp.frame$queue)

計算結果の表示

待ち行列時系列データの真ん中1/3を取り出し、トランザクション到着時のトランザクション数、待ち行列長を集計している。比較のため、それらの理論値も計算・表示している。

##############
# 計算結果の表示
##############

# 前後1/3を切り落とし
n <- nrow(trs.time.sequence)
calc.frame <- trs.time.sequence[(n/3):(n*2/3),]

# 到着率とサービス率から稼働率の理論値を計算
(rho <- lambda / mu)
# システム内の平均トランザクション数の理論値
(L <- rho / (1 - rho))
# 平均待ち行列長の理論値
(Lq <- rho^2 / (1 - rho))
# 平均トランザクションタイム
L / lambda
# 平均待ち時間
Lq / lambda

# トランザクション数、待ち行列長、総所要時間、待ち時間の平均値を表示
page(c(
mean(calc.frame$transactions),
mean(calc.frame$queue),
mean(calc.frame$trs.time),
mean(calc.frame$queue.time)
))

##############

# 計算結果の表示

##############

# 前後1/3を切り落とし

n <- nrow(trs.time.sequence)

calc.frame <- trs.time.sequence[(n/3):(n*2/3),]

# 到着率とサービス率から稼働率の理論値を計算

(rho <- lambda / mu)

# システム内の平均トランザクション数の理論値

(L <- rho / (1 - rho))

# 平均待ち行列長の理論値

(Lq <- rho^2 / (1 - rho))

# 平均トランザクションタイム

L / lambda

# 平均待ち時間

Lq / lambda

# トランザクション数、待ち行列長、総所要時間、待ち時間の平均値を表示

page(c(

mean(calc.frame$transactions),

mean(calc.frame$queue),

mean(calc.frame$trs.time),

mean(calc.frame$queue.time)

))

計算結果

1000個のデータからトランザクション数、待ち行列長を10回計算させ、それらについて割り戻したλの逆数、各データの平均と標準偏差を計算した。

ρ = 0.5のケース

λ = 1/10、μ = 1/5、ρ = 0.5のケース。平均トランザクション数と平均待ち行列長の理論値は、L = 1、L_q = 0.5で、これらに対する待ち時間はT = 10、T_w = 5。

トランザクション数に関する計算結果は、かなり理論値と整合している。

	L	T	1/λ
1	0.977022977	9.767519297	9.997225783
2	1.181818182	12.00225815	10.1557569
3	1.236763237	11.35299611	9.17960348
4	0.87012987	9.097838003	10.45572427
5	0.943056943	9.652253196	10.23506933
6	1.132867133	11.09199315	9.791080377
7	0.958041958	9.28812046	9.694899459
8	1.347652348	12.61173676	9.358301328
9	1.058941059	10.13796162	9.573678846
10	0.867132867	9.19585645	10.60489897
AVG	1.057342657	10.41985332	9.854755454
STD	0.162710928	1.258385656	0.467315969

待ち行列についても、整合性は良い。

	L_q	T_q	1/λ
1	0.460539461	4.687171936	10.17756856
2	0.632367632	6.669065267	10.54618378
3	0.686313686	6.311337813	9.195995853
4	0.391608392	4.163816097	10.63260182
5	0.471528472	4.72111758	10.01237012
6	0.634365634	6.030695282	9.506655083
7	0.465534466	4.447464396	9.553458927
8	0.785214785	7.437052562	9.471360832
9	0.564435564	5.262195935	9.322934744
10	0.367632368	4.099711426	11.1516607
AVG	0.545954046	5.382962829	9.859736125
STD	0.136420649	1.159489377	0.655334793

ρ = 0.9のケース

λ = 1/10、μ = 1/9、ρ = 0.9のケース。平均トランザクション数と平均待ち行列長の理論値は、L = 9、L_q = 8.1で、これらに対する待ち時間はT = 90、T_w = 81。

トランザクション数に関する計算結果は、理論値よりも大きく出ている。

	L	T	1/λ
1	10.11288711	100.5733569	9.945068678
2	12.03096903	120.0280761	9.97659256
3	15.71128871	162.6168804	10.35032093
4	10.998002	110.2958229	10.02871457
5	18.26373626	178.496846	9.773293013
6	7.716283716	77.4353613	10.03531806
7	6.178821179	62.23838321	10.07285717
8	9.491508492	95.64553268	10.07695803
9	6.951048951	70.34023525	10.11936986
10	6.073926074	63.43794238	10.44430597
AVG	10.35284715	104.1108437	10.05625237
STD	4.076793696	40.26529308	0.192915047

待ち行列長についても傾向は同じ。

	L_q	T_q	1/λ
1	9.204795205	91.66512812	9.95841038
2	11.13286713	110.9692603	9.967716221
3	14.76723277	152.9773707	10.35924422
4	10.07392607	101.1184062	10.03763631
5	17.28271728	169.1669214	9.7882132
6	6.789210789	68.44424425	10.08132556
7	5.254745255	53.24239678	10.13225079
8	8.545454545	86.43775829	10.11505682
9	6.06993007	61.37562417	10.11142195
10	5.220779221	54.59901247	10.4580198
AVG	9.434165834	94.99961227	10.06974161
STD	4.051237304	40.07040651	0.193152208

稼働率をρが1に近づくと、計算結果に乖離がみられる。たとえばN = 10000個のデータについて計算してみても、傾向は変わらない。

TauStation

タグ: 待ち行列

待ち行列(M/M/1)の再現 – イベント制御

考え方