前提
時刻t~t + Δtの間に以下のいずれかの状態遷移が発生するとする。希少性の仮定から、2つ以上の事象が同時に起こることはなく、いずれか1つが発生するとする。
- 確率λΔtで1つのトランザクションが到着する
- 確率μΔtで1つのサービスが完了する
- 確率(1 – λΔt – μΔt)でトランザクションの到着もなくサービスも完了しない
- 本来は(1 – λΔt)(1 – μΔt)で表されるところ、これを展開してΔt2の項を無視してこの形になる
- あるいは指数分布の密度関数をMaclaurin展開して2時以上の項をo(Δt2)として消していってもよい
なお、M/M/1待ち行列のイベント制御による再現をR言語で試している。
状態方程式
システムの状態を、システム内のトランザクション数nで表す。nには、サービスを受けているトランザクションとサービスを待機しているトランザクションの数の和。
時刻tにおいてトランザクション数がnである状態確率をpn(t)とすると、状態方程式は以下のようになる。
(1) ![]()
まず式(1)の第1式について、
(2) 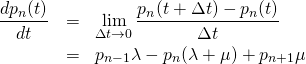
また第2式については、
(3) 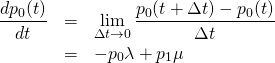
(4) 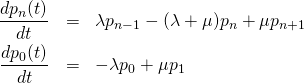
定常問題化と状態方程式の解
状態方程式においてt → ∞でトランザクション数の変化がなく一定値に収束するとして、次式を得る。
(5) ![]()
ここでρ = λ/μ < 0とおいて、
(6) ![]()
これは階差数列の式に変形できて、
(7) ![]()
上式から順次各項を求めると、
(8) 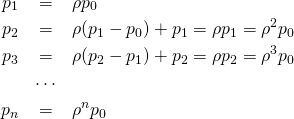
全事象の和が1という条件から、以下の結果を得る。
(9) 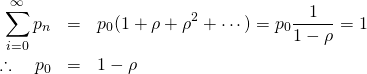
これより、システムの状態がnである確率は以下で表せる。
(10) ![]()
ρの意味
ρ = λ / μは、単位時間当たりのサービス提供数に対する単位時間当たりのトラフィック到達数で、サービスの混み具合を表している。また、どの程度サービスが稼働しているか/利用されているか、とも言えるので、混雑度、平均稼働率/利用率、平均到達率、平均トラフィック密度などと呼ばれている。
平均トランザクション数と平均待ち行列長
システム内の平均トランザクション数Lは、
(11) 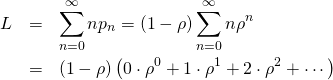
これを以下のように解く。
(12) 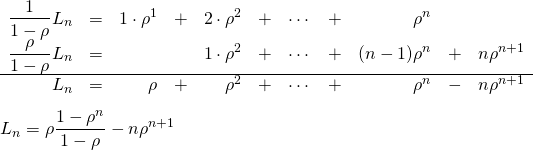
よって、
(13) ![]()
また平均待ち行列長については、サービス中のトランザクションを除いて考えて、
(14) ![]()
これも以下のように解く。
(15) 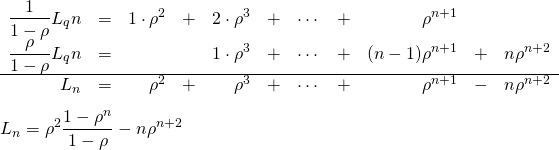
よって、
(16) ![]()
リトルの法則(Litter’s law)
定常状態にある待ち行列において、トランザクションがシステムに到着してからサービスを終えるまでの時間の平均(平均応答時間)をTとすると、その間に平均してλTのトランザクションが到着することから、次式が成り立つ。
(17) ![]()
また、同じことが待ち行列長Lqと平均待ち時間Tqにも言えるので、
(18) ![]()
リトルの公式を使うと、待ち行列の長さと到着率から、平均待ち時間が計算できる。
(19) 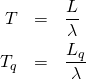
たとえば客の列に到着したときの行列の人数を数え、その後到着する客の数や出ていく客の数から到着率を推定することで、待ち時間を推定できる。