Dフリップフロップ

2023-01-15 / tau / コメントする

概要

Dラッチは、入力Gが1になっている間入力D（データ）の値を出力Qに出し続ける。一方入力Gにクロックパルスが与えられる場合、入力データの値をクロックパルスの立ち上がりで一度だけ記憶・出力して、次のクロックの立ち上がりまでその出力を保持したいときには、Dラッチではうまくいかない。

Dフリップフロップはこのような場合に使う。Dフリップフロップ回路は、以下の様にDラッチを2つ連ねた形をしている。

この回路は、CLKの入力が0→1に立ち上がった時のDの値を保持し、次に再びCLKが0→1に立ち上がるまでその値を保持し続ける。

基本的なDフリップフロップは以下のようなシンボルで表される。

仕組み

前段・後段それぞれのラッチのGに与える信号を反転させているのがミソで、以下のような流れになる。

クロックレベルが0のときは前段のラッチが入力状態、後段のラッチが保持状態となる
- 前段のラッチは入力の値を出力し続ける
- 後段のラッチは前段の値に関わらず保持内容を出力し続ける
クロックレベルが1になると、前段のラッチが保持状態、後段のラッチが出力状態になる
- 前段のラッチはそれまでの入力内容を保持する
- 後段のラッチは前段の保持内容を出力し始める
再びクロックレベルが0になっても、後段のラッチは前のステップで入力された値を保持し続ける

イメージで図にすると以下の様になるだろうか。

回路図での確認

Dフリップフロップの動作を回路図で確認すると以下の流れになる。

初期状態として、すべての端子の信号レベルが0の状態とする。このとき前段のG1への入力のみ反転して1となり、前段のラッチは出力状態、後段のラッチは保持状態となっている。

その状態で入力が1となった場合。前段が出力状態となり1を出力するが、後段は保持状態のため、最後の出力は変化しない。

ここでクロックが1となると、前段が保持状態、後段が出力状態となり、最後の出力が１に変わる。クロックが1の間に入力値が変化しても、立ち上がり時の値が前段で保持されているので、出力は変わらない。

その後クロックが0となると、後段が保持状態となり、最後の出力が維持される。

その後入力信号が0となっても、後段で保持されている値が出力され続ける。

タイミングチャート

Dフリップフロップの動作をタイミングチャートで見てみた。下図の緑／オレンジの色がついている部分が前段／後段がSetの状態、色がついていない部分がそれぞれのHoldの状態。

各ステップでの状態は以下の様に推移する。

Step	CLK	入力	前段の状態	前段の出力	後段の状態	後段の出力
a	0	0	Set	0	Hold	0
b	0	1	Set	1	Hold	0
c	1	1	Hold	1	Set	1
d	0	1	Set	1	Hold	1
e	0	0	Set	0	Hold	1
f	1	0	Hold	0	Set	0
g	1	1	Hold	0	Set	0
h	0	1	Set	1	Hold	0

Dラッチ

2023-01-13 / tau / コメントする

Dラッチ（D-Rarch)回路は以下のような回路。

この回路の動作は以下の様になる。

G=0の間、(Q, Q̄)は保持される
G=1の間、Q = D、(Q, Q̄) = D̄

このラッチはゲートGのレベルが0の間は値を保持し続け、Gが1になると入力Dの値をそのままQに出力する。このことを左の回路で確認する。

回路後段はRSフリップフロップとよく似ていて、入力にNOTゲートを入れればRSフリップフロップになる。ちょうど回路前段がNANDゲートになっているので、これをANDゲートとNOTゲートに分ければ、以下の様に表現できる。

次に回路前段の動作について考える。入力の0と1の組み合わせに対して、出力は以下の様になる。

この結果とRSフリップフロップの動作を合わせると、以下のような真理値表になる。

Gが0の間、QとQ̄を保持
Gが1の間、QにはDが出力され、Q̄にはD̄が出力される

たとえば以下のようなタイミングチャートになるか。

RSフリップフロップ

2023-01-12 / tau / コメントする

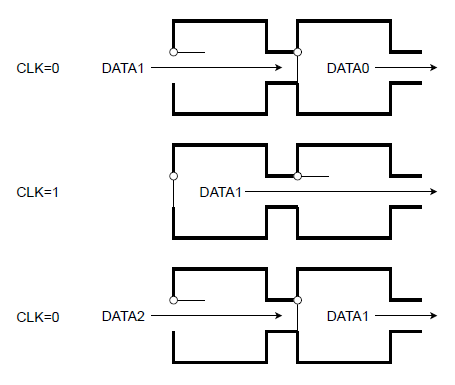
RSフリップフロップの動作

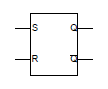
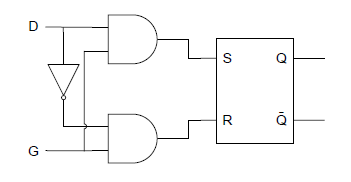
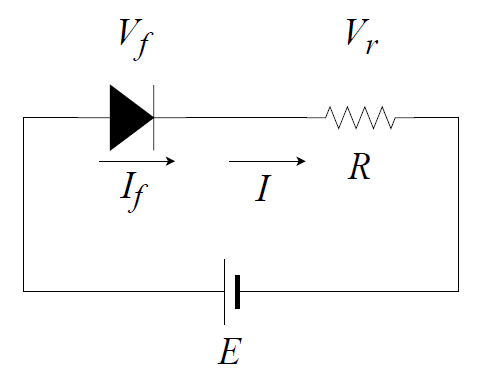
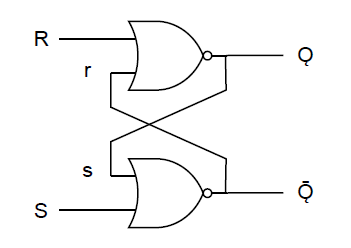
今まで横目でやり過ごしていたフリップフロップ回路について整理してみた。以下のようなRSフリップフロップを考える。

S	R	Ǫ	Ǭ
0	0	保持	保持
0	1	0	1
1	0	1	0
1	1	禁止

一般には(S, R)の入力が(1, 0)や(0, 1)のように与えられたとき、以下のように説明されているものが多い。

たとえばS = 1のとき、Ǭ側のNORゲートの出力は0 で確定
その結果r = 0となり、R = 0の入力と合わせて、Ǫ側のNORゲートの出力は1となる

ただ、以下のような点が気になった。

そもそも入力が1の方が必ず先に動くのか
電源投入時などにǪやǬの値が不定になったときにどうなるのか

何せ素人なので半導体素子の中でどういうタイミングで何が起こっているのかよくわからないが、自分なりに追ってみることにした。

あまりうまくない例

まず、(S, R)が（禁止されている(1, 1)の組み合わせの場合も含めて）与えられたとき、(Ǫ, Ǭ)の値が予めいろいろなパターンをとっていたとして、その後の推移を確かめてみた。

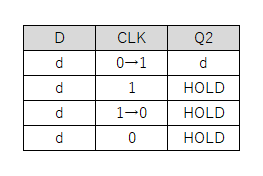
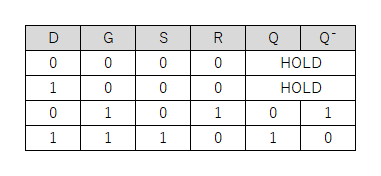
以下の表は、そのような時の状態変化を追ってみたもの。(Ǫ, Ǭ)の出力が確定しているので、与えられた(S, R)との組み合わせで(r, s)にフィードバックされる値が変化していくと考えた。

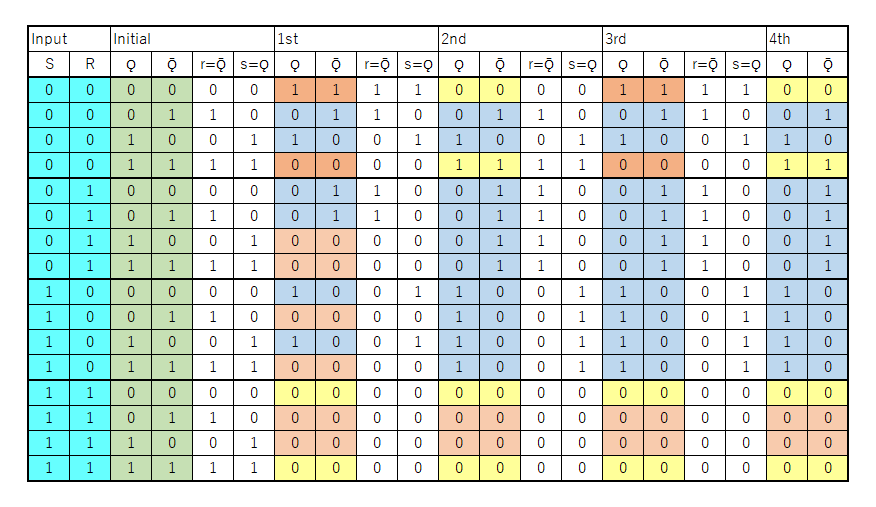
この表からは、以下の様なことが読み取れる。

(R, S)が(0, 1)や(1, 0)のときは、2サイクル目以降想定される出力で安定
(R, S)が(0, 0)のときは
- (Ǫ, Ǭ)が(0, 1)や(1, 0)のときは1サイクル目から元の値が保持される
- (Ǫ, Ǭ)が(0, 0)や(1, 1)のときには振動する
(R, S)が(1, 1)のときには(Ǫ, Ǭ)が(0, 0)になる

ここでも以下のようなことが気になる。

(Ǫ, Ǭ)が(0, 1)や(1, 0)のときに(R, S)に同じパターンを入れると、1サイクルだけ(R, S) = (0, 0)の状態になるが、これはナノ秒のレベルで実際に起こることなのか
(Ǫ, Ǭ)が(0, 0)のときに(S, R)に(0, 0)や(1, 1)を入力すると、その後(Ǫ, Ǭ)がごく短周期で振動するが、実際にそうなのか

そこで、回路のゲート単位で実行順序が変わった場合にどういう結果になるか確認してみた。

回路レベルで追った例

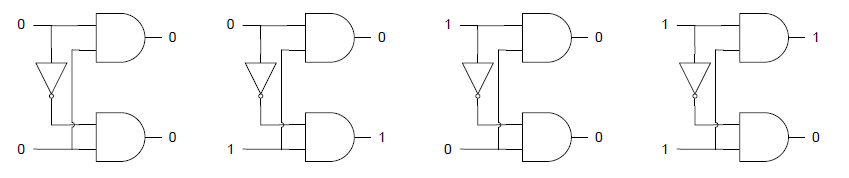
入力と出力が同じパターンの場合

一つ目は、(S, R)に(Ǫ, Ǭ)と同じパターンを入力した場合。以下の例では(Ǫ, Ǭ) = (0, 1)のときに(S, R) = (0, 1)を入力したケース。

まず上の方のゲートが先に動作した場合、以下の様に変化する。

入力Rが変化したとき、上のゲートが動作するが下のゲートの入力sへの帰還入力は変化しない
ここで入力Sが変化していたとして下のゲートが動作しても、出力は変わらない
以後、安定状態に達する

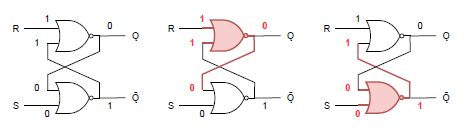
また下のゲートが先に動いた場合も同じ流れで、結果は同じになる。

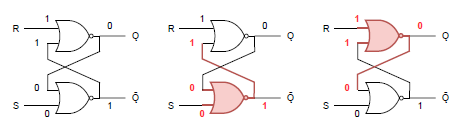
パターンが逆の場合も、回路は対称なので同じ流れになる。

入力と出力のパターンが逆の場合

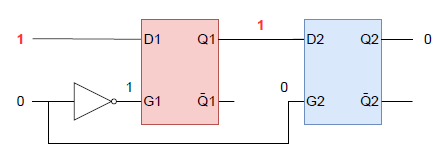
二つ目は、(S, R)に(Ǫ, Ǭ)と逆のパターンを入力した場合。以下の例では(Ǫ, Ǭ) = (0, 1)のときに(S, R) = (1, 0)を入力したケース。これは少しややこしい、

入力Rが変化したとき上のゲートが動作するが、その出力と下のゲートの入力sは変化しない
入力Sが変化したとき下のゲートが動作し、その出力と上のゲートへの帰還入力は1→0に変化する
それにつれて上のゲートが動作し、出力と帰還入力sは1に変化する
それにつれて下のゲートが動作するが、その出力と上のゲートへの帰還入力0は変化しない
以後、安定状態に達する

一方、下のゲートが先に動作した場合は、すぐそのあとに下のゲートが動作して安定する。

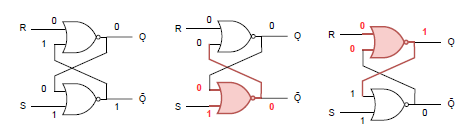
出力保持の場合

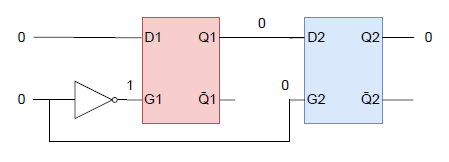
入力(S, R)が(0, 0)の場合は出力は保持されるが、これを確認する。

以下の例では上のゲート、下のゲートの何れが動作するときも状態は変化せず、出力は変わらずに安定する。出力が逆のパターンでも、対称性から同じように保持される。

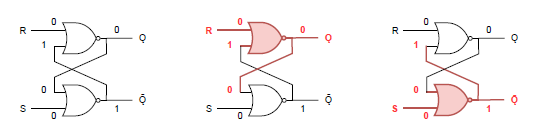
禁止状態の場合

最後に、禁止されている(S, R) = (1, 1)を入力した場合を確認する。以下の例では元の出力が(0, 1)の場合を例にしているが、入力の何れも1なので、有限のサイクルで必ず(Ǫ, Ǭ) = (0, 0)となる。

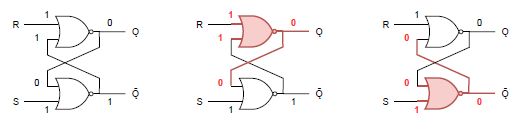
問題はその後に(S, R) = (0, 0)の保持信号を入力したときで、同じ状態から始めても最初に動作するゲートによって結果が異なってしまう。

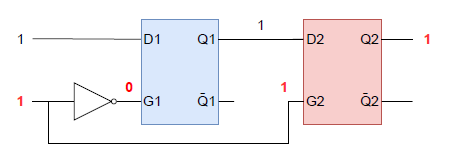
まず、以下は上のゲートが最初に動作した場合。結果は(Ǫ, Ǭ) = (1, 0)となる。

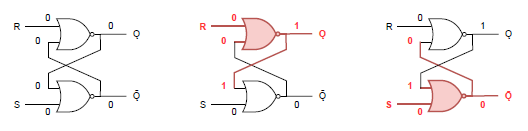
一方下のゲートが最初に動作した場合は、結果が逆の(Ǫ, Ǭ) = (0, 1)になる。

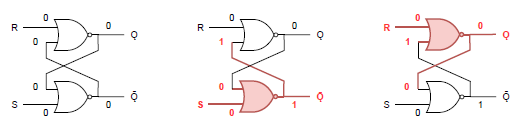
したがって、(S, R) = (1, 1)が禁止されている背景を整理すると以下の様になる。

(S, R) = (1, 1)を入力すると、結果は必ず(Ǫ, Ǭ) = (0, 0)になる。
このパターンは(Ǫ, Ǭ)が符号通りの否定関係にならない
その後、そのパターンに対して(S, R) = (0, 0)の保護信号を入力した場合、結果が一つに特定できない

以上のことから、ゲートの動作順序レベル（入力信号の到達時刻レベル）の違いに対して、RSフリップフロップの論理値表の意義が一定理解できた。

RSフリップフロップの回路構成

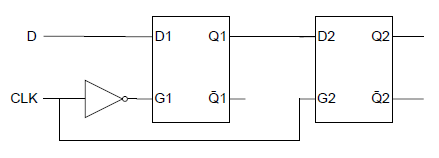
RSフリップフロップは、NORゲートで表現される場合とNANDゲートで表現される場合がある。それらについての覚え書き。

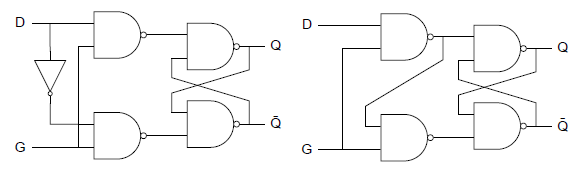
冒頭のNORゲートによるRSフリップフロップ回路は以下の通り。

NORゲートは入力が否定ゲートのANDゲートと等価なので、以下の様になる。

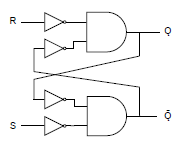
ANDゲートをNANDゲートに変え、出力を変えない様にすると以下の様になる。

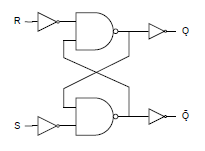
最終段のNOTゲートを除き、Ǫと Ǭを反転させて以下を得る。入力と出力の配置がNORゲートと逆になるが、S (Set)とがǬが同じ側に来るので直感的にわかりやすい。

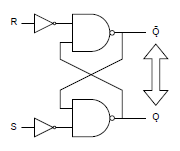
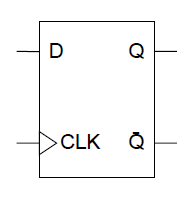
RSフリップフロップは、以下のような記号で表される。

LEDの保護抵抗

2023-01-09 / tau / コメントする

対象とする回路

以下のような回路を考える。

ここで各記号の意味は以下の通り。

E：電源電圧
V_f：LEDにかかる順電圧
I_f：LEDを流れる順電圧
V_r：保護抵抗による電圧降下
R：保護抵抗値
I：回路を流れる電流（I = I_f）

V_f（順電圧）やI_f（順電流）は、それらを用いる人や場合によってLEDが発光し始める閾値や典型値など定義が異なっているが、ここではその時点の回路での値とする。

保護抵抗による電圧降下

保護抵抗による電圧降下、抵抗値、回路電流の間では、以下のようにオームの法則が成立する。V_rはIの線形関数となっている。

(1) $\begin{equation*} V_r = R I \end{equation*}$

LEDの特性

一方LEDの順電圧V_fも電流の関数だが、それは一般的な固定抵抗のものと異なり、電圧によって非線形的に電流が変化する。以下は赤色LEDの特性曲線を概ねのイメージで描いた例。

LEDの電流～電圧特性の特徴は以下の通り。

LEDにかかる順電圧がある閾値を越えるまでは電流は流れず発光しない
順電圧が閾値を越えると、電圧値に対して急に電流が増加する
順電圧の僅かな変動に対して、順電流の変動が大きい

LEDの内部抵抗で考えると以下のように表現できる。

閾値以下ではLEDの内部抵抗は∞と考えてもよいくらい大きい
閾値を越えると、順電圧の増加に対して内部抵抗が急激に減少していく

回路に関する計算

基礎式

LEDの順電流・順電圧に関する特性曲線をI = I_f(V_f)という関数で表し、電源とLEDの内部抵抗をゼロとして考えると、回路全体の電圧のバランスは以下のようになる。

(2) $\begin{equation*} E = V_f + RI = V_f + R I_f(V_f) \end{equation*}$

これをIfについて解くと以下のようになる。

(3) $\begin{equation*} R = \dfrac{E - V_f}{I_f(V_f)} \end{equation*}$

I_fがV_fの関数になっているのでややこしいが、一般にはデータシートの典型値などをそのまま用いて計算する例が多い。たとえば電源電圧が3.3Vで赤色LEDを発光させる場合、典型値としてI_fTYP=20mAの時にV_fTYP=2Vという値が示されているとすると保護抵抗値は以下のようになる。

(4) $\begin{equation*} R = \dfrac{3.3 - 2}{0.02} = 65 \Omega \end{equation*}$

よく見かける保護抵抗値は100Ωとか330Ωといった値だが、こういう場合のV_fやI_fがどのようになるか、また順電流を10mAや30mAにしたい場合抵抗値をどうするかといったことを知りたい場合は非線形な方程式を解かなければならない。

特性曲線にの読み取りによる計算

LEDの特性が先に示したような特性曲線のように与えられている場合、電源電圧3.3Vに対して順電流をI_f = 10mAとしたい場合は、グラフからV_f =2.4V程度となるので、保護抵抗値は以下のように求められる。

(5) $\begin{equation*} R = \dfrac{3.3 - 2.4}{0.01} = 90 \Omega \end{equation*}$

順電流の絶対最大定格値が30mAの場合、これを越えないようにするための最低の保護抵抗値はどうなるか。先の特性曲線からI_f = 30mAに対してV_f = 2.6V程度と読み取れるので、以下のように計算される。

(6) $\begin{equation*} R = \dfrac{3.3 - 2.6}{0.03} \fallingdotseq 23.33 \Omega \end{equation*}$

市販のLEDのデータ

市販のLEDのデータシートの値の例は以下のようになっていた。なおA社のデータシートによると、より長期間使用するために順電流値を10～30mAの間で使用することが推奨されている。

これらのLEDを典型値で用いる場合の保護抵抗値を計算してみる。A社の赤、青・緑のLEDを5Vで使う場合、

(7) $\begin{equation*} \left\{ \begin{align} \dfrac{5 - 2.1}{0.02} &= 145 \Omega \\ \dfrac{5 - 3.4}{0.02} &= 80 \Omega \end{align} \end{equation*}$

またB社の赤、緑のLEDを3.3Vで使う場合、

(8) $\begin{equation*} \left\{ \begin{align} \dfrac{3.3 - 1.9}{0.01} &= 140 \Omega \\ \dfrac{3.3 - 2}{0.01} &= 130 \Omega \end{align} \end{equation*}$

なお各LEDのI_fとV_fの関係をデータシートの特性曲線から典型値で読み取ってみると以下のようになり、概ね表の値に一致する。

A社の赤LED→20mAに対して約2.13V
A社の緑・青LED→20mAに対して約3.4V
B社の赤LED→10mAに対して1.9V

不明LEDの特性曲線

Raspberry Pi用のキットにはパーツのデータシートや型番などがなく、LEDの特性も分からない。そこで、抵抗値を取り換えながらV_fやV_rを計測し、I_fの計算値をプロットしてみた。
データシートで見られるカーブの形をしており、赤・緑・黄色の特性が近く、青と白はより大きなV_fを必要としている。

特性曲線は指数関数で近似できるので、片対数軸で表示してみる。若干指数関数よりもV_fに対するI_fの増加率が緩やかな傾向がある。

Excelの分析ツールでも指数関数近似をしてくれるが、ここで以下の式形で回帰をしてみた。まず以下の式で回帰する。

(9) $\begin{equation*} I_f = a e^{b V_f} \end{equation*}$

一般にはa(exp(b V_f) – 1)の形で示されているが、回帰計算のしやすさのために形を少し変えている。両辺の対数をとって線形回帰する。

(10) $\begin{equation*} \ln I_f = \ln a + b V_f \end{equation*}$

結果は分析ツールのグラフと同じ形で以下のようになる。

片対数で表すと以下のようになる。

対数軸で線形性が良好な緑と黄は元の関数形でもよく一致しているが、赤と青・白についてはV_fが大きいところでの乖離が大きくなる。ただしV_fに対してI_fが小さく推定されるため、たまたまとはいえ安全側になっている。

各色のLEDに対する推定式の定数は以下のようになった。

対数化した線形式での相関係数は0.978～0.999程度であり、かなり高い。土質・地質工学や水理学のように自然現象を扱う場合とは異なる。

なお、I_fを希望する値にするための抵抗値は以下のように計算できる。

(11) $\begin{equation*} I_f = a \exp{b V_f} = a \exp{b (E - R I_f)} \end{equation*}$

この式をRについて解いて、

(12) $\begin{equation*} R = \dfrac{E - \dfrac{1}{b} \ln \dfrac{I_f}{a}}{I_f} \end{equation*}$

I_fを変化させた場合、各色のLEDに使う保護抵抗値は以下のように計算される。

キットのテキストでは220Ωの抵抗をよく用いているが、その場合は赤・緑・黄色が7～8mA程度、青と白では4mA程度ということになる。実際、青と白のLEDは少し暗めかなというくらいの明るさなので、これらの計算結果は腹落ちできる。

7セグメントLED

2023-01-03 / tau / コメントする

配置図

7セグメントLEDのピン配置は以下の通り（コモンカソードの場合）。

セグメントコード

各セグメントを0で消灯、1で点灯するとして、a～g及びDPを逆順にして0～Fを表示させるビット配列は以下のようになる。

表示	dp g f e d c b a	Hex
0	00111111	0x3f
1	00000110	0x06
2	01011011	0x5b
3	01001111	0x4f
4	01100110	0x66
5	01101101	0x6d
6	01111101	0x7d
7	00000111	0x07
8	01111111	0x7f
9	01101111	0x6f
A	01110111	0x77
B	01111100	0x7c
C	00111001	0x39
D	01011110	0x5e
E	01111001	0x79
F	01110001	0x71

GPIOに直接接続

7セグメントLEDの動作を確認するため、以下の様にRaspberry Pi 4BのGPIOに接続した。

点灯テストは以下のコードで行った。

LEDの各ピンにGPIOのピンを割り当て
0～9, A～Fの表示に対応するビットパターンを定義
- ビット配列はdp, g, f, e, d, c, b, aの逆順
16個のパターンを0.5秒ずつ表示
パターン表示はビット配列を必要分だけシフトして、ピンに対応するビットが1の場合にセグメントを点灯、0の場合に消灯
終了時に全セグメントを消灯

import RPi.GPIO as GPIO
import time

# Assign pins of 7-segment LED to GPIO pins
led = {'a':2, 'b':3, 'c':4, 'd':5, 'e':6, 'f':7, 'g':8, 'dp':9}
# Dfine inverted bit patterns of 0, ..., 9, A, ..., F (dp,g,f,e,d,c,b,a)
patterns = [0x3f, 0x06, 0x5b, 0x4f, 0x66, 0x6d, 0x7d, 0x07, 0x7f, 0x6f, 0x77, 0x7c, 0x39, 0x5e, 0x79, 0x71]

# Define function to call before ending
def destroy():
    for pin in led.values():
        GPIO.output(pin, GPIO.LOW)

# Start execution
GPIO.setmode(GPIO.BCM)

# Light off all segments
for pin in led.values():
    GPIO.setup(pin, GPIO.OUT, initial=GPIO.LOW)

# Light each pattern 0.5sec
for pattern in patterns:
    # Decode each bit of a pattern and send the level to GPIO pin
    for n, pin in enumerate(led.values()):
        if (pattern >> n) & 1:
            GPIO.output(pin, GPIO.HIGH)
        else:
            GPIO.output(pin, GPIO.LOW)
        print(pattern)
    time.sleep(0.5)

destroy()

import RPi.GPIO as GPIO

import time

# Assign pins of 7-segment LED to GPIO pins

led = {'a':2, 'b':3, 'c':4, 'd':5, 'e':6, 'f':7, 'g':8, 'dp':9}

# Dfine inverted bit patterns of 0, ..., 9, A, ..., F (dp,g,f,e,d,c,b,a)

patterns = [0x3f, 0x06, 0x5b, 0x4f, 0x66, 0x6d, 0x7d, 0x07, 0x7f, 0x6f, 0x77, 0x7c, 0x39, 0x5e, 0x79, 0x71]

# Define function to call before ending

def destroy():

for pin in led.values():

GPIO.output(pin, GPIO.LOW)

# Start execution

GPIO.setmode(GPIO.BCM)

# Light off all segments

for pin in led.values():

GPIO.setup(pin, GPIO.OUT, initial=GPIO.LOW)

# Light each pattern 0.5sec

for pattern in patterns:

# Decode each bit of a pattern and send the level to GPIO pin

for n, pin in enumerate(led.values()):

if (pattern >> n) & 1:

GPIO.output(pin, GPIO.HIGH)

else: