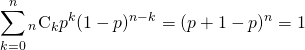irisデータの俯瞰

2020-03-13 / tau / コメントする

概要

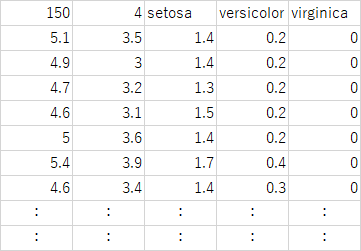
irisデータは3つのアヤメの種類(setosa, versicolor, varginica)の150個体について、萼(sepal)と花弁(petal)の長さと幅の組み合わせ4つの特徴量のデータを提供する。これらについて一般的なグラフによる可視化によって俯瞰してみる。

特徴量の分布

クラス分けしない場合

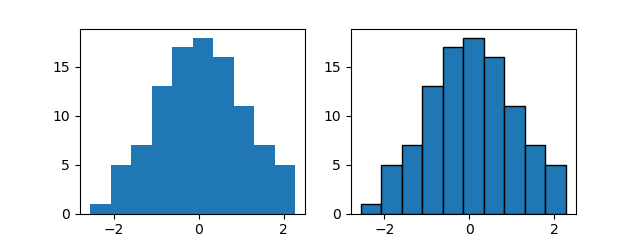
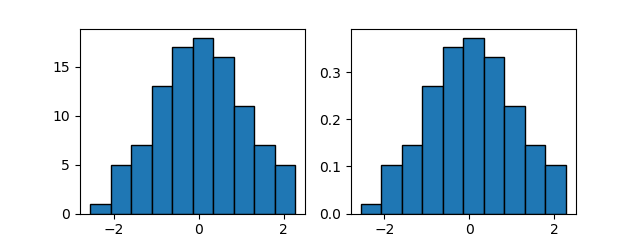
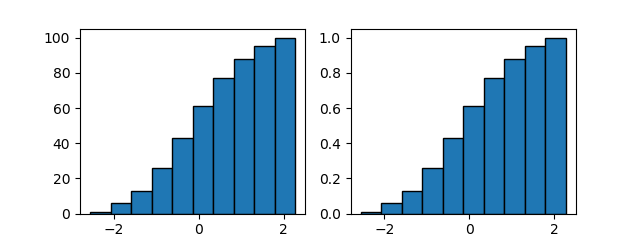
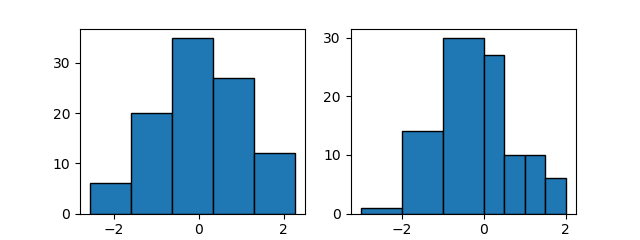
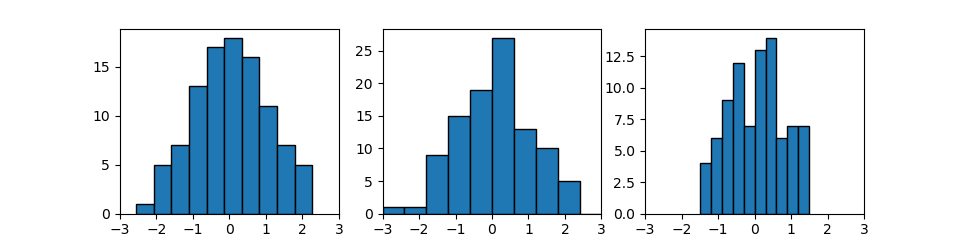
まずアヤメの150個体における4つの特徴量について、3つの種類を区別せずにその分布を見てみる。

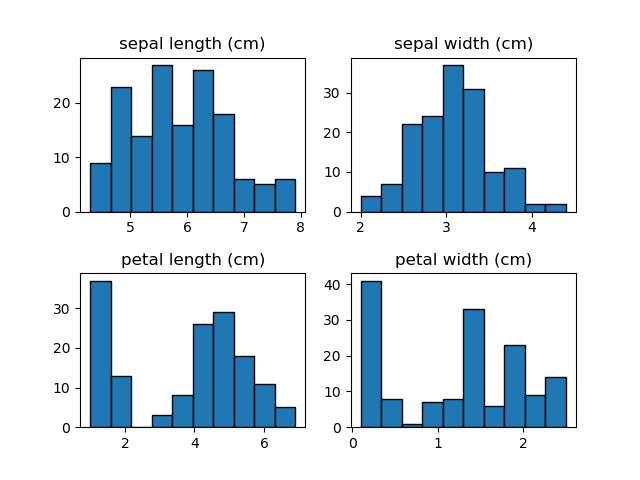
この結果を見る限り特に際立った特徴は見いだせない。敢えて言うなら、萼の長さは若干ばらつきが大きく、萼の幅は割合”きれいな”分布。花弁については、長さ・幅とも値の小さいところで独立した分布が見られる。

このデータが異なる種類のものが混在したものだと知っていれば、花弁の独立した分布は特定の種類のものかもしれないと推測できるくらい。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris

iris_data = load_iris()

feature_names = iris_data['feature_names']
X = iris_data['data']
n_data, n_features = X.shape

fig, axs = plt.subplots(2, 2, figsize=(6.4, 4.8))
ax_1d = [ax for row in axs for ax in row]

fig.subplots_adjust(hspace=0.4)

for feature in range(n_features):
    ax_1d[feature].set_title(feature_names[feature])
    ax_1d[feature].hist(X[:, feature], ec='k')

plt.show()

import numpy as np

import matplotlib.pyplot as plt

from sklearn.datasets import load_iris

iris_data = load_iris()

feature_names = iris_data['feature_names']

X = iris_data['data']

n_data, n_features = X.shape

fig, axs = plt.subplots(2, 2, figsize=(6.4, 4.8))

ax_1d = [ax for row in axs for ax in row]

fig.subplots_adjust(hspace=0.4)

for feature in range(n_features):

ax_1d[feature].set_title(feature_names[feature])

ax_1d[feature].hist(X[:, feature], ec='k')

plt.show()

クラス分けした場合

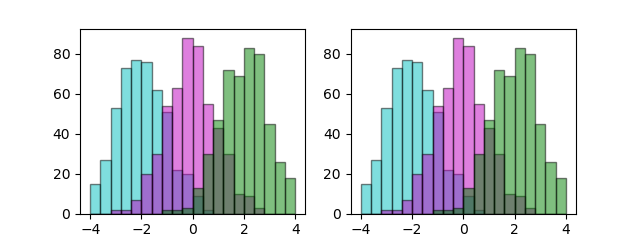
次に4つの特徴量について、3つの種類ごとに分けて表示してみる。

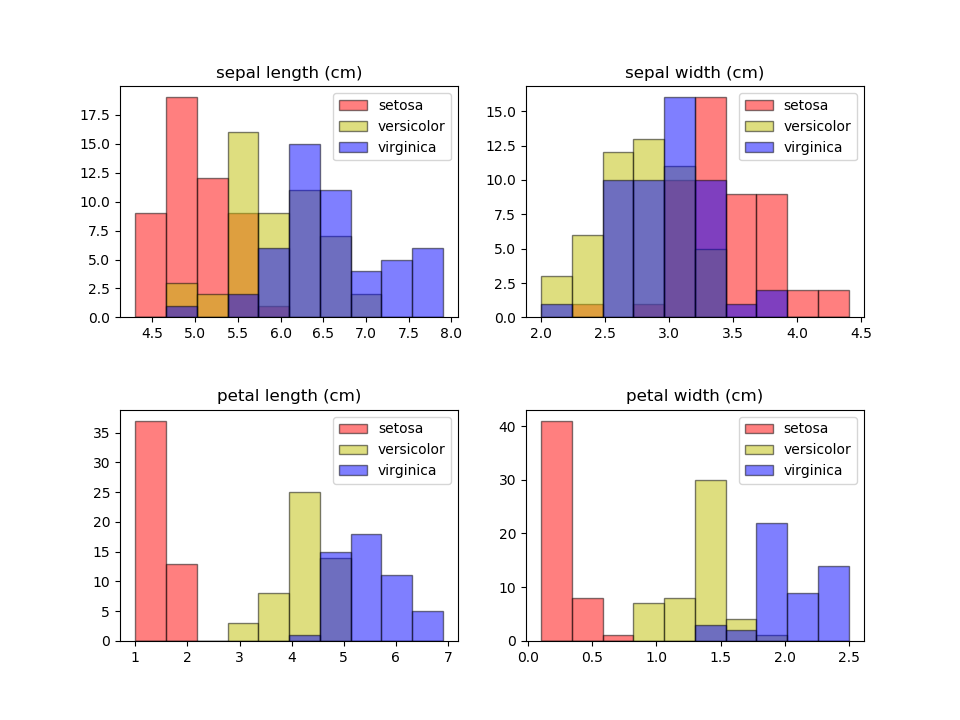
こうすると少し特徴が見えてくる。

花弁の独立した分布はsetosa(ヒオウギアヤメ)のものであることがわかり、額の長さの分布がばらついているのは、複数の種類の特徴量が少しずつずれて重なっているからだということもわかる。

この分布だけだと、花弁の長さ2.5cm、花弁の幅が0.7～0.8cmあたりから小さいと、アヤメの種類はsetosaと特定できそうだが、versicolorとvirginicaは重なっていて、花弁の幅が1.75cmあたりで分けると少し誤判定はあるが概ね分けられそうである。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris

iris_data = load_iris()

feature_names = iris_data['feature_names']
species_names = iris_data['target_names']
X = iris_data['data']
y = iris_data['target']
n_data, n_features = X.shape
species = np.sort(np.array(list(set(y))))

fig, axs = plt.subplots(2, 2, figsize=(9.6, 7.2))
ax_1d = [ax for row in axs for ax in row]

fig.subplots_adjust(hspace=0.4)

colors = ['r', 'y', 'b']
for feature in range(n_features):
    ax_1d[feature].set_title(feature_names[feature])
    feature_data = X[:, feature]
    range_max = np.max(feature_data)
    range_min = np.min(feature_data)
    for sp in species:
        ax_1d[feature].hist(feature_data[y==sp],
                            range=(range_min, range_max), bins=10,
                            color=colors[sp], ec='k', alpha=0.5,
                            label=species_names[sp])
        ax_1d[feature].legend()

plt.show()

import numpy as np

import matplotlib.pyplot as plt

from sklearn.datasets import load_iris

iris_data = load_iris()

feature_names = iris_data['feature_names']

species_names = iris_data['target_names']

X = iris_data['data']

y = iris_data['target']

n_data, n_features = X.shape

species = np.sort(np.array(list(set(y))))

fig, axs = plt.subplots(2, 2, figsize=(9.6, 7.2))

ax_1d = [ax for row in axs for ax in row]

fig.subplots_adjust(hspace=0.4)

colors = ['r', 'y', 'b']

for feature in range(n_features):

ax_1d[feature].set_title(feature_names[feature])

feature_data = X[:, feature]

range_max = np.max(feature_data)

range_min = np.min(feature_data)

for sp in species:

ax_1d[feature].hist(feature_data[y==sp],

range=(range_min, range_max), bins=10,

color=colors[sp], ec='k', alpha=0.5,

label=species_names[sp])

ax_1d[feature].legend()

plt.show()

2つの特徴量同士の関係

比較例

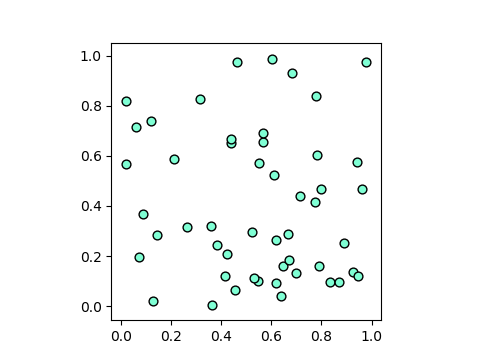
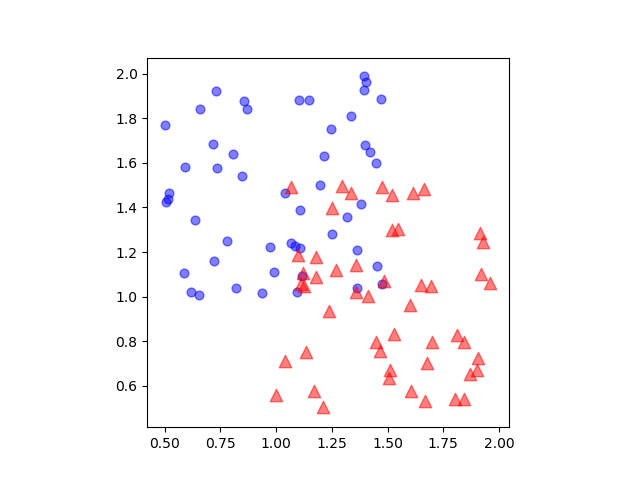
例として、萼の長さと萼の幅、萼の長さと花弁の幅、それぞれの間の関係をプロットしてみる。

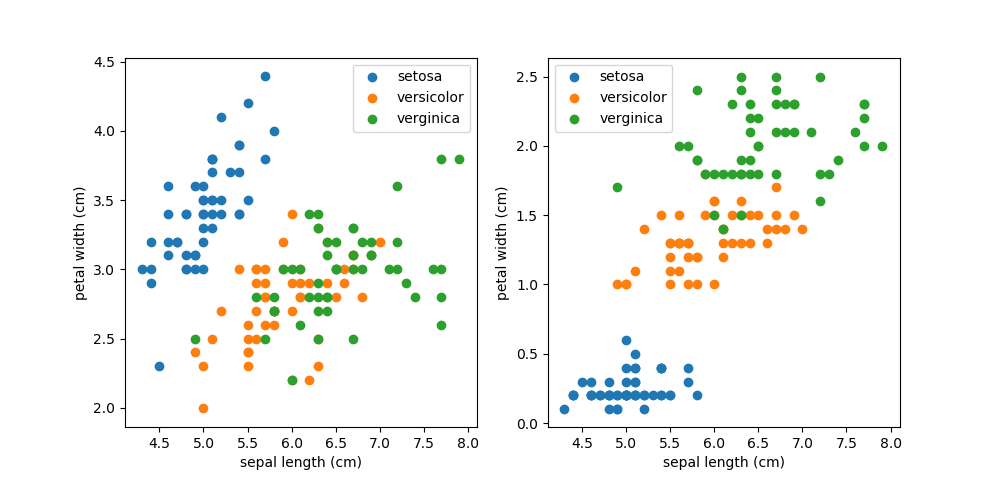
萼の長さと花弁の長さの関係を見ると、setosaは明らかに独立したグループだが、versicolorとverginicaは混ざり合っていて分離できそうにない。先ほどのヒストグラムでは、萼の長さ、萼の幅それぞれだけではversicolorとvirginicaは区分できなかった。2次元でプロットするとそれらがうまく区分する可能性もあるが、この場合はうまくいかないようである。

一方、萼の長さと花弁の長さの関係を比べると、versicolorとversinicaも何とか区分できそうである。よくみると、この3つの区分は萼の長さと関係なく、花弁の幅のみで概ね区分できそうである。これも先ほどの花弁の幅のヒストグラムの結果と符合する。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris

iris_data = load_iris()
X = iris_data['data']
y = iris_data['target']

data_setosa = X[y==0]
data_versicolor = X[y==1]
data_verginica = X[y==2]

sl, sw, pl, pw = (0, 1, 2, 3)

fig, axs = plt.subplots(1, 2, figsize=(10, 4.8))

a, b = (sl, sw)
axs[0].scatter(data_setosa[:, a], data_setosa[:, b], label="setosa")
axs[0].scatter(data_versicolor[:, a], data_versicolor[:, b], label="versicolor")
axs[0].scatter(data_verginica[:, a], data_verginica[:, b], label="verginica")

a, b = (sl, pw)
axs[1].scatter(data_setosa[:, a], data_setosa[:, b], label="setosa")
axs[1].scatter(data_versicolor[:, a], data_versicolor[:, b], label="versicolor")
axs[1].scatter(data_verginica[:, a], data_verginica[:, b], label="verginica")

for ax in axs:
    ax.set_xlabel(iris_data.feature_names[a])
    ax.set_ylabel(iris_data.feature_names[b])

    ax.legend()

plt.show()

import numpy as np

import matplotlib.pyplot as plt

from sklearn.datasets import load_iris

iris_data = load_iris()

X = iris_data['data']

y = iris_data['target']

data_setosa = X[y==0]

data_versicolor = X[y==1]

data_verginica = X[y==2]

sl, sw, pl, pw = (0, 1, 2, 3)

fig, axs = plt.subplots(1, 2, figsize=(10, 4.8))

a, b = (sl, sw)

axs[0].scatter(data_setosa[:, a], data_setosa[:, b], label="setosa")

axs[0].scatter(data_versicolor[:, a], data_versicolor[:, b], label="versicolor")

axs[0].scatter(data_verginica[:, a], data_verginica[:, b], label="verginica")

a, b = (sl, pw)

axs[1].scatter(data_setosa[:, a], data_setosa[:, b], label="setosa")

axs[1].scatter(data_versicolor[:, a], data_versicolor[:, b], label="versicolor")

axs[1].scatter(data_verginica[:, a], data_verginica[:, b], label="verginica")

for ax in axs:

ax.set_xlabel(iris_data.feature_names[a])

ax.set_ylabel(iris_data.feature_names[b])

ax.legend()

plt.show()

`scatter_matrix`による確認

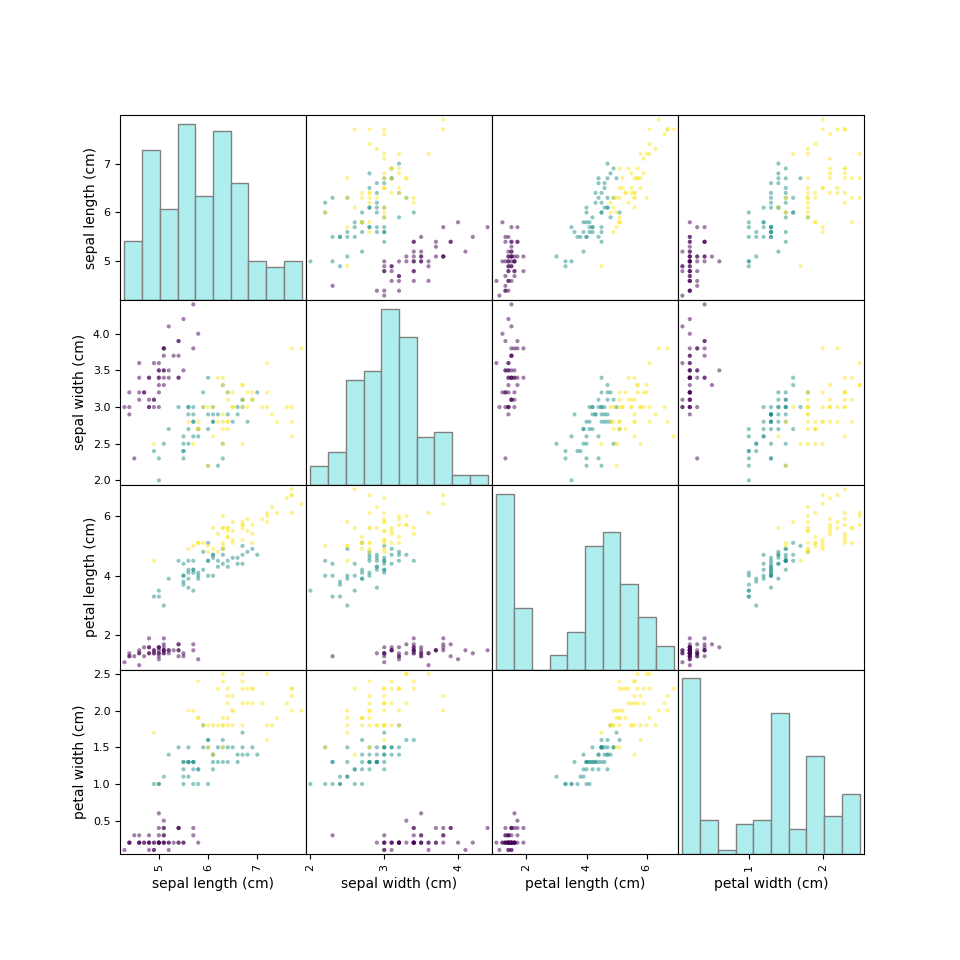
上記のような特徴量の組み合わせは、特徴量がn個の場合には_nC₂通りとなる。irisデータの場合、特徴量は4つだから6個の特徴量ペアがあり得る。pandasのscatter_matrixを利用すると、このような特徴量のペアについて網羅的に確認できる。

ただしscatter_matrixでは、対角要素のヒストグラムを特徴量ごとに分けることはできないようだ。

import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris

iris_dataset = load_iris()

iris_dataframe = pd.DataFrame(iris_dataset.data,
                              columns=iris_dataset.feature_names)

pd.plotting.scatter_matrix(iris_dataframe,
                           figsize=(9.6, 9.6),
                           c=iris_dataset.target,
                           hist_kwds={'ec':'gray', 'color':'paleturquoise'})

plt.show()

import pandas as pd

import matplotlib.pyplot as plt

from sklearn.datasets import load_iris

iris_dataset = load_iris()

iris_dataframe = pd.DataFrame(iris_dataset.data,

columns=iris_dataset.feature_names)

pd.plotting.scatter_matrix(iris_dataframe,

figsize=(9.6, 9.6),

c=iris_dataset.target,

hist_kwds={'ec':'gray', 'color':'paleturquoise'})

plt.show()

`pairplot`による確認

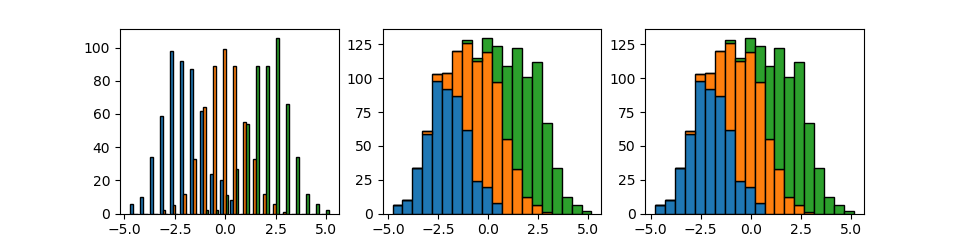
seabornのpairplotを使うと、対角要素に各特徴量ごとの頻度分布／密度分布を表示することができる。pairplotの場合、ターゲットの品種を文字列で与えるとそれに従った色分けをしてくれて、対角要素の密度分布も品種ごとに分けてくれる。

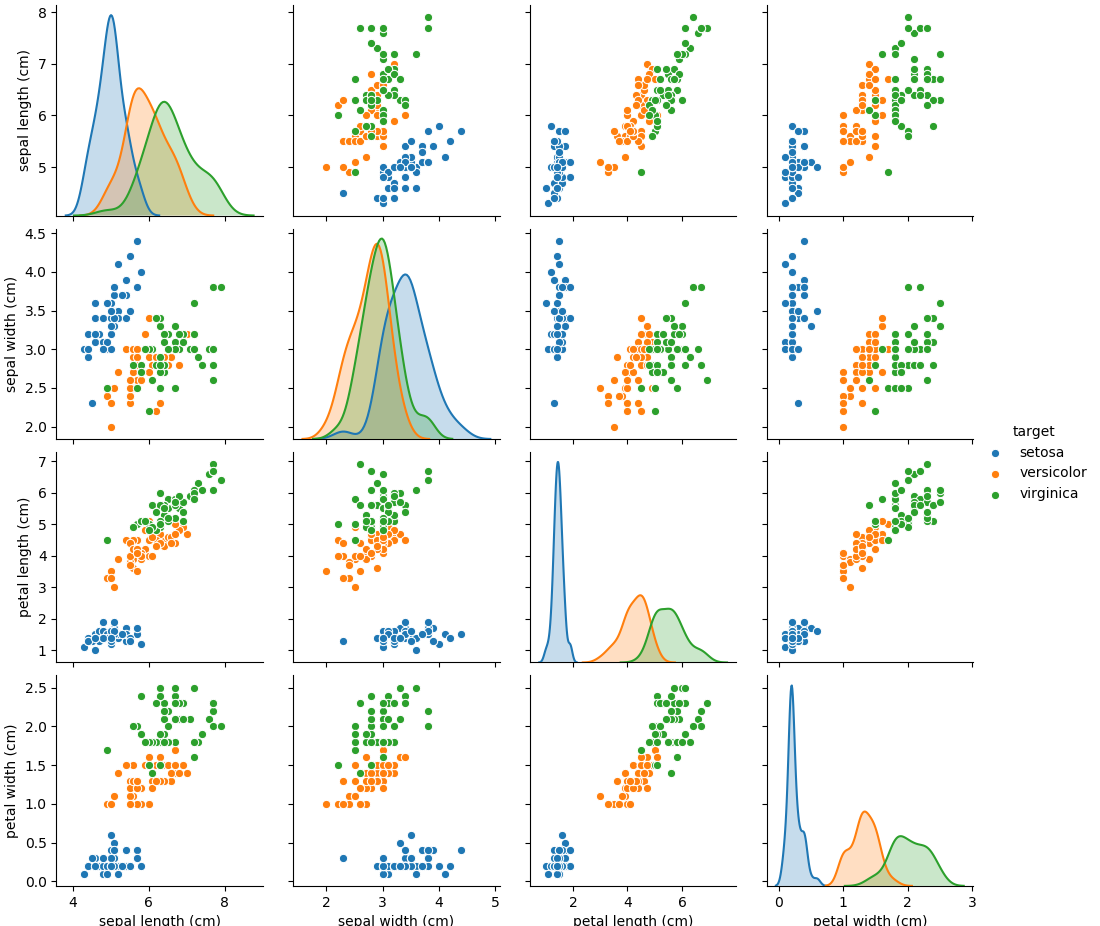
ペアプロットの結果から、3つの種類は複数の散布図で比較的きれいにグループとなっていることがわかる。

import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.datasets import load_iris

iris_ds = load_iris()
df = pd.DataFrame(iris_ds.data, columns=iris_ds.feature_names)

df['target'] = iris_ds.target
df.loc[df['target']==0, 'target'] = "setosa"
df.loc[df['target']==1, 'target'] = "versicolor"
df.loc[df['target']==2, 'target'] = "virginica"

g = sns.pairplot(df, hue='target')
g.fig.set_figheight(9.6)
g.fig.set_figwidth(11)

plt.show()

import pandas as pd

import matplotlib.pyplot as plt

import seaborn as sns

from sklearn.datasets import load_iris

iris_ds = load_iris()

df = pd.DataFrame(iris_ds.data, columns=iris_ds.feature_names)

df['target'] = iris_ds.target

df.loc[df['target']==0, 'target'] = "setosa"

df.loc[df['target']==1, 'target'] = "versicolor"

df.loc[df['target']==2, 'target'] = "virginica"

g = sns.pairplot(df, hue='target')

g.fig.set_figheight(9.6)

g.fig.set_figwidth(11)

plt.show()

3つの特徴量の関係

最後に、4つの特徴量のうち3つを取り出して3次元の散布図で表示してみる。2次元の散布図ではversicolorとvirginicaで若干の重なりがあるが、3次元化するときれいに分かれるかもしれない。

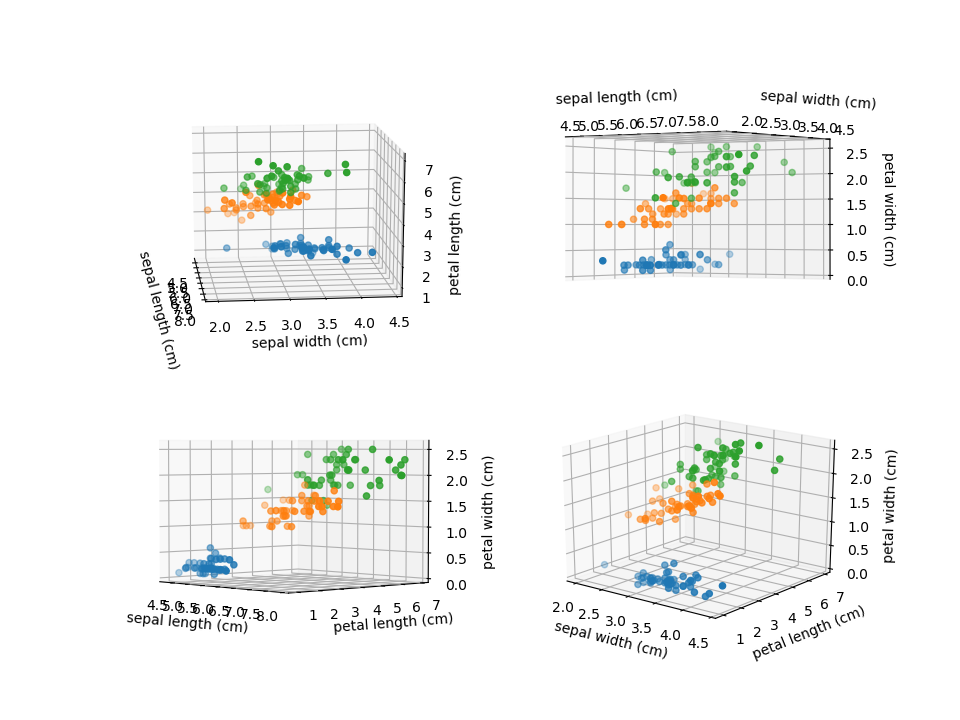
3次元空間で見ても若干の重なりはあるが、2つの特徴量だけの時に比べて、よりグループ分離の精度が高まることは期待できそうだ。

考えてみれば、アヤメの品種区分のように特徴量が少ない場合のクラス分類問題は、1次元の頻度分布、2次元・3次元の頻度分布のように次元を増やして確認ができれば、区分は比較的容易なように思われる。一方で人の間隔では3次元を認識するのがやっとなので、特徴量の数が増えた時には太刀打ちできない。

畢竟、機械学習・AIとは人間が認識制御困難な多数の特徴量＝多次元における判別や相関を如何に実行するかというところなのでは、と思われる。

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from sklearn.datasets import load_iris

iris_ds = load_iris()

X = iris_ds.data
y = iris_ds.target
feature_names = iris_ds.feature_names

sl, sw, pl, pw = (0, 1, 2, 3)
species = (0, 1, 2)

combinations = np.array([
    [sl, sw, pl],
    [sl, sw, pw],
    [sl, pl, pw],
    [sw, pl, pw]
])

fig = plt.figure(figsize=(9.6, 7.2))

ax1 = fig.add_subplot(221, projection='3d')
ax2 = fig.add_subplot(222, projection='3d')
ax3 = fig.add_subplot(223, projection='3d')
ax4 = fig.add_subplot(224, projection='3d')
axs = [ax1, ax2, ax3, ax4]

for ax, comb in zip(axs, combinations):
    f0, f1, f2 = comb[0], comb[1], comb[2]
    xs, ys, zs = X[:, f0], X[:, f1], X[:, f2]
    for sp in species:
        ax.scatter(xs[y==sp], ys[y==sp], zs[y==sp])
    ax.set_xlabel(feature_names[f0])
    ax.set_ylabel(feature_names[f1])
    ax.set_zlabel(feature_names[f2])

plt.show()

import numpy as np

import matplotlib.pyplot as plt

from mpl_toolkits.mplot3d import Axes3D

from sklearn.datasets import load_iris

iris_ds = load_iris()

X = iris_ds.data

y = iris_ds.target

feature_names = iris_ds.feature_names

sl, sw, pl, pw = (0, 1, 2, 3)

species = (0, 1, 2)

combinations = np.array([

[sl, sw, pl],

[sl, sw, pw],

[sl, pl, pw],

[sw, pl, pw]

])

fig = plt.figure(figsize=(9.6, 7.2))

ax1 = fig.add_subplot(221, projection='3d')

ax2 = fig.add_subplot(222, projection='3d')

ax3 = fig.add_subplot(223, projection='3d')

ax4 = fig.add_subplot(224, projection='3d')

axs = [ax1, ax2, ax3, ax4]

for ax, comb in zip(axs, combinations):

f0, f1, f2 = comb[0], comb[1], comb[2]

xs, ys, zs = X[:, f0], X[:, f1], X[:, f2]

for sp in species:

ax.scatter(xs[y==sp], ys[y==sp], zs[y==sp])

ax.set_xlabel(feature_names[f0])

ax.set_ylabel(feature_names[f1])

ax.set_zlabel(feature_names[f2])

plt.show()

matplotlib.pyplot.scatter – 散布図

2020-03-10 / tau / コメントする

概要

scatterはx座標とy座標のペアを与えて散布図を描く。

scatter(x, y, color/c=color, s=n, marker=marker, edgecolors=color): x、yは散布図の点の座標で、数値の場合は1点、配列の場合は複数の点を描く。color(またはc)とedgecolorはmatplotlibのcolor指定。markerはmatplotlibのmarkers指定。sはマーカーのサイズ。

基本形

import numpy as np
import numpy.random as rnd
import matplotlib.pyplot as plt

rnd.seed(0)
x = rnd.random(50)
y = rnd.random(50)

fig, ax = plt.subplots(figsize=(4.8, 3.6))

ax.scatter(x, y, s=40, marker='o', color='aquamarine', edgecolors='black')

ax.set_aspect('equal')

plt.show()

import numpy as np

import numpy.random as rnd

import matplotlib.pyplot as plt

rnd.seed(0)

x = rnd.random(50)

y = rnd.random(50)

fig, ax = plt.subplots(figsize=(4.8, 3.6))

ax.scatter(x, y, s=40, marker='o', color='aquamarine', edgecolors='black')

ax.set_aspect('equal')

plt.show()

複数系列

複数系列の場合は、系列ごとにscatterを実行する。

import numpy as np
import numpy.random as rnd
import matplotlib.pyplot as plt

x1 = rnd.random(50) + 0.5
y1 = rnd.random(50) + 1

x2 = rnd.random(50) + 1
y2 = rnd.random(50) + 0.5

fig, ax = plt.subplots(figsize=(6.4, 4.8))

ax.scatter(x1, y1, marker='o', s=40, c='blue', alpha=0.5)
ax.scatter(x2, y2, marker='^', s=80, color='red', alpha=0.5)

ax.set_aspect('equal')

plt.show()

import numpy as np

import numpy.random as rnd

import matplotlib.pyplot as plt

x1 = rnd.random(50) + 0.5

y1 = rnd.random(50) + 1

x2 = rnd.random(50) + 1

y2 = rnd.random(50) + 0.5

fig, ax = plt.subplots(figsize=(6.4, 4.8))

ax.scatter(x1, y1, marker='o', s=40, c='blue', alpha=0.5)

ax.scatter(x2, y2, marker='^', s=80, color='red', alpha=0.5)

ax.set_aspect('equal')

plt.show()

Irisデータセット

2020-03-08 / tau / コメントする

概要

Irisデータセットはアヤメの種類と特徴量に関するデータセットで、3種類のアヤメの花弁と萼(がく)に関する特徴量について多数のデータを提供する。

ここではPythonのscikit-learnにあるirisデータの使い方をまとめる。

データの取得とデータ構造

Pythonで扱う場合、scikit-learnのdatasetsモジュールにあるload_iris()でデータを取得できる。データはBunchクラスのオブジェクトととのことだが、通常の扱い方は辞書と同じようだ。

from sklearn.datasets import load_iris

iris_dataset = load_iris()

for key, value in zip(iris_dataset.keys(), iris_dataset.values()):
    print("{}:\n{}\n".format(key, value))

from sklearn.datasets import load_iris

iris_dataset = load_iris()

for key, value in zip(iris_dataset.keys(), iris_dataset.values()):

print("{}:\n{}\n".format(key, value))

データの構造は辞書型で、150個体のアヤメに関する特徴量の配列と各個体の種類、種類名などが格納されている。

data:
[[5.1 3.5 1.4 0.2]
 [4.9 3.  1.4 0.2]
 [4.7 3.2 1.3 0.2]
 .....
 [6.5 3.  5.2 2. ]
 [6.2 3.4 5.4 2.3]
 [5.9 3.  5.1 1.8]]

target:
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2
 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
 2 2]

target_names:
['setosa' 'versicolor' 'virginica']

DESCR:
.. _iris_dataset:

Iris plants dataset
--------------------

**Data Set Characteristics:**

    :Number of Instances: 150 (50 in each of three classes)
    :Number of Attributes: 4 numeric, predictive attributes and the class
    :Attribute Information:
        - sepal length in cm
        - sepal width in cm
        - petal length in cm
        - petal width in cm
        - class:
                - Iris-Setosa
                - Iris-Versicolour
                - Iris-Virginica
                
    :Summary Statistics:

    ============== ==== ==== ======= ===== ====================
                    Min  Max   Mean    SD   Class Correlation
    ============== ==== ==== ======= ===== ====================
    sepal length:   4.3  7.9   5.84   0.83    0.7826
    sepal width:    2.0  4.4   3.05   0.43   -0.4194
    petal length:   1.0  6.9   3.76   1.76    0.9490  (high!)
    petal width:    0.1  2.5   1.20   0.76    0.9565  (high!)
    ============== ==== ==== ======= ===== ====================

    :Missing Attribute Values: None
    :Class Distribution: 33.3% for each of 3 classes.
    :Creator: R.A. Fisher
    :Donor: Michael Marshall (MARSHALL%PLU@io.arc.nasa.gov)
    :Date: July, 1988

The famous Iris database, first used by Sir R.A. Fisher. The dataset is taken
from Fisher's paper. Note that it's the same as in R, but not as in the UCI
Machine Learning Repository, which has two wrong data points.

This is perhaps the best known database to be found in the
pattern recognition literature.  Fisher's paper is a classic in the field and
is referenced frequently to this day.  (See Duda & Hart, for example.)  The
data set contains 3 classes of 50 instances each, where each class refers to a
type of iris plant.  One class is linearly separable from the other 2; the
latter are NOT linearly separable from each other.

.. topic:: References

   - Fisher, R.A. "The use of multiple measurements in taxonomic problems"
     Annual Eugenics, 7, Part II, 179-188 (1936); also in "Contributions to
     Mathematical Statistics" (John Wiley, NY, 1950).
   - Duda, R.O., & Hart, P.E. (1973) Pattern Classification and Scene Analysis.
     (Q327.D83) John Wiley & Sons.  ISBN 0-471-22361-1.  See page 218.
   - Dasarathy, B.V. (1980) "Nosing Around the Neighborhood: A New System
     Structure and Classification Rule for Recognition in Partially Exposed
     Environments".  IEEE Transactions on Pattern Analysis and Machine
     Intelligence, Vol. PAMI-2, No. 1, 67-71.
   - Gates, G.W. (1972) "The Reduced Nearest Neighbor Rule".  IEEE Transactions
     on Information Theory, May 1972, 431-433.
   - See also: 1988 MLC Proceedings, 54-64.  Cheeseman et al"s AUTOCLASS II
     conceptual clustering system finds 3 classes in the data.
   - Many, many more ...

feature_names:
['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)', 'petal width (cm)']

filename:
C:\Users\tomo\AppData\Local\Programs\Python\Python37-32\lib\site-packages\sklearn\datasets\data\iris.csv

data:

[[5.1 3.5 1.4 0.2]

[4.9 3. 1.4 0.2]

[4.7 3.2 1.3 0.2]

.....

[6.5 3. 5.2 2. ]

[6.2 3.4 5.4 2.3]

[5.9 3. 5.1 1.8]]

target:

[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0

0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1

1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2

2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2

2 2]

target_names:

['setosa' 'versicolor' 'virginica']

DESCR:

.. _iris_dataset:

Iris plants dataset

--------------------

**Data Set Characteristics:**

:Number of Instances: 150 (50 in each of three classes)

:Number of Attributes: 4 numeric, predictive attributes and the class

:Attribute Information:

- sepal length in cm

- sepal width in cm

- petal length in cm

- petal width in cm

- class:

- Iris-Setosa

- Iris-Versicolour

- Iris-Virginica

:Summary Statistics:

============== ==== ==== ======= ===== ====================

Min Max Mean SD Class Correlation

============== ==== ==== ======= ===== ====================

sepal length: 4.3 7.9 5.84 0.83 0.7826

sepal width: 2.0 4.4 3.05 0.43 -0.4194

petal length: 1.0 6.9 3.76 1.76 0.9490 (high!)

petal width: 0.1 2.5 1.20 0.76 0.9565 (high!)

============== ==== ==== ======= ===== ====================

:Missing Attribute Values: None

:Class Distribution: 33.3% for each of 3 classes.

:Creator: R.A. Fisher

:Donor: Michael Marshall (MARSHALL%PLU@io.arc.nasa.gov)

:Date: July, 1988

The famous Iris database, first used by Sir R.A. Fisher. The dataset is taken

from Fisher's paper. Note that it's the same as in R, but not as in the UCI

Machine Learning Repository, which has two wrong data points.

This is perhaps the best known database to be found in the

pattern recognition literature. Fisher's paper is a classic in the field and

is referenced frequently to this day. (See Duda & Hart, for example.) The

data set contains 3 classes of 50 instances each, where each class refers to a

type of iris plant. One class is linearly separable from the other 2; the

latter are NOT linearly separable from each other.

.. topic:: References

- Fisher, R.A. "The use of multiple measurements in taxonomic problems"

Annual Eugenics, 7, Part II, 179-188 (1936); also in "Contributions to

Mathematical Statistics" (John Wiley, NY, 1950).

- Duda, R.O., & Hart, P.E. (1973) Pattern Classification and Scene Analysis.

(Q327.D83) John Wiley & Sons. ISBN 0-471-22361-1. See page 218.

- Dasarathy, B.V. (1980) "Nosing Around the Neighborhood: A New System

Structure and Classification Rule for Recognition in Partially Exposed

Environments". IEEE Transactions on Pattern Analysis and Machine

Intelligence, Vol. PAMI-2, No. 1, 67-71.

- Gates, G.W. (1972) "The Reduced Nearest Neighbor Rule". IEEE Transactions

on Information Theory, May 1972, 431-433.

- See also: 1988 MLC Proceedings, 54-64. Cheeseman et al"s AUTOCLASS II

conceptual clustering system finds 3 classes in the data.

- Many, many more ...

feature_names:

['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)', 'petal width (cm)']

filename:

C:\Users\tomo\AppData\Local\Programs\Python\Python37-32\lib\site-packages\sklearn\datasets\data\iris.csv

データのキーは以下のようになっている。

from sklearn.datasets import load_iris

iris_dataset = load_iris()

print(iris_dataset.keys())

# dict_keys(['data', 'target', 'target_names', 'DESCR', 'feature_names', 'filename'])

from sklearn.datasets import load_iris

iris_dataset = load_iris()

print(iris_dataset.keys())

# dict_keys(['data', 'target', 'target_names', 'DESCR', 'feature_names', 'filename'])

データの内容

`'data'`～特徴量データセット

150個体のアヤメに関する、4つの特徴量をレコードとしたデータセット。各個体の4つの特徴量の配列を要素とした2次元配列。列のインデックス(0, 1, 2, 3)が四つの特徴量に対応している。

'data': array([[5.1, 3.5, 1.4, 0.2],
       [4.9, 3. , 1.4, 0.2],
       [4.7, 3.2, 1.3, 0.2],
       [4.6, 3.1, 1.5, 0.2],
       [5. , 3.6, 1.4, 0.2],
       .....
       [6.7, 3. , 5.2, 2.3],
       [6.3, 2.5, 5. , 1.9],
       [6.5, 3. , 5.2, 2. ],
       [6.2, 3.4, 5.4, 2.3],
       [5.9, 3. , 5.1, 1.8]])

'data': array([[5.1, 3.5, 1.4, 0.2],

[4.9, 3. , 1.4, 0.2],

[4.7, 3.2, 1.3, 0.2],

[4.6, 3.1, 1.5, 0.2],

[5. , 3.6, 1.4, 0.2],

.....

[6.7, 3. , 5.2, 2.3],

[6.3, 2.5, 5. , 1.9],

[6.5, 3. , 5.2, 2. ],

[6.2, 3.4, 5.4, 2.3],

[5.9, 3. , 5.1, 1.8]])

`'target'`～アヤメの種類に対応したコード

3種類のアヤメに対応した0～2のコードの配列。150個体のアヤメに対応した1次元配列。

'target': array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
       1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
       1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
       2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
       2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2])

'target': array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,

0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,

0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,

1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,

1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,

2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,

2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2])

`'target_names'`～アヤメの種類名

アヤメの3つの種類の種類名。stosaは「ヒオウギアヤメ」といって少し大人締めの色形だが、versicolorとvirginicaは素人にはその違いがよく分からない。

'target_names': array(['setosa', 'versicolor', 'virginica'], dtype='<U10'),

1	'target_names': array(['setosa', 'versicolor', 'virginica'], dtype='<U10'),

種類名とコードの関係は以下の通り。

setosa	0
versicolor	1
virginica	2

`'feature_names'`～特徴名

データの格納順はDESCRの後。アヤメの種類のクラス分けに使う特徴。

sepal(萼)とpetal(花弁)の長さと幅、計4つの特徴の名称が、単位cmを含む文字列で格納されている。

‘sepal length (cm)’　萼の長さ
‘sepal width (cm)’　萼の幅
‘petal length (cm)’　花弁の長さ
‘petal width (cm)’　花弁の幅

'feature_names': ['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)', 'petal width (cm)']

1	'feature_names': ['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)', 'petal width (cm)']

特徴名とコードの関係は以下の通り。

sepal length (cm)	0
sepal width (cm)	1
petal length (cm)	2
petal width (cm)	3

`'filename'`～ファイル名

これも格納順はDESCRの後で、CSVファイルの位置が示されている。1行目にはデータ数、特徴量数、特徴量名称が並んでおり、その後に150行のアヤメの個体に対する4列の特徴量と1列の種類データが格納されている。このファイルにはfeature_namesやDESCRに当たるデータは格納されていない。

'filename': 'C:...lib\\site-packages\\sklearn\\datasets\\data\\iris.csv'

1	'filename': 'C:...lib\\site-packages\\sklearn\\datasets\\data\\iris.csv'

`'DESCR'`～データセットの説明

データセットの説明。print(iris_dataset['DESCR'])のようにprint文で整形表示される。

レコード数は150個(3つのクラスで50個ずつ)
属性は、4つの数値属性とクラス(種類)
→predictiveの意味とclassが単数形なのがわからない

.. _iris_dataset:

Iris plants dataset
--------------------

**Data Set Characteristics:**

    :Number of Instances: 150 (50 in each of three classes)
    :Number of Attributes: 4 numeric, predictive attributes and the class
    :Attribute Information:
        - sepal length in cm
        - sepal width in cm
        - petal length in cm
        - petal width in cm
        - class:
                - Iris-Setosa
                - Iris-Versicolour
                - Iris-Virginica
                
    :Summary Statistics:

    ============== ==== ==== ======= ===== ====================
                    Min  Max   Mean    SD   Class Correlation
    ============== ==== ==== ======= ===== ====================
    sepal length:   4.3  7.9   5.84   0.83    0.7826
    sepal width:    2.0  4.4   3.05   0.43   -0.4194
    petal length:   1.0  6.9   3.76   1.76    0.9490  (high!)
    petal width:    0.1  2.5   1.20   0.76    0.9565  (high!)
    ============== ==== ==== ======= ===== ====================

    :Missing Attribute Values: None
    :Class Distribution: 33.3% for each of 3 classes.
    :Creator: R.A. Fisher
    :Donor: Michael Marshall (MARSHALL%PLU@io.arc.nasa.gov)
    :Date: July, 1988

The famous Iris database, first used by Sir R.A. Fisher. The dataset is taken
from Fisher's paper. Note that it's the same as in R, but not as in the UCI
Machine Learning Repository, which has two wrong data points.

This is perhaps the best known database to be found in the
pattern recognition literature.  Fisher's paper is a classic in the field and
is referenced frequently to this day.  (See Duda & Hart, for example.)  The
data set contains 3 classes of 50 instances each, where each class refers to a
type of iris plant.  One class is linearly separable from the other 2; the
latter are NOT linearly separable from each other.

.. topic:: References

   - Fisher, R.A. "The use of multiple measurements in taxonomic problems"
     Annual Eugenics, 7, Part II, 179-188 (1936); also in "Contributions to
     Mathematical Statistics" (John Wiley, NY, 1950).
   - Duda, R.O., & Hart, P.E. (1973) Pattern Classification and Scene Analysis.
     (Q327.D83) John Wiley & Sons.  ISBN 0-471-22361-1.  See page 218.
   - Dasarathy, B.V. (1980) "Nosing Around the Neighborhood: A New System
     Structure and Classification Rule for Recognition in Partially Exposed
     Environments".  IEEE Transactions on Pattern Analysis and Machine
     Intelligence, Vol. PAMI-2, No. 1, 67-71.
   - Gates, G.W. (1972) "The Reduced Nearest Neighbor Rule".  IEEE Transactions
     on Information Theory, May 1972, 431-433.
   - See also: 1988 MLC Proceedings, 54-64.  Cheeseman et al"s AUTOCLASS II
     conceptual clustering system finds 3 classes in the data.
   - Many, many more ...

.. _iris_dataset:

Iris plants dataset

--------------------

**Data Set Characteristics:**

:Number of Instances: 150 (50 in each of three classes)

:Number of Attributes: 4 numeric, predictive attributes and the class

:Attribute Information:

- sepal length in cm

- sepal width in cm

- petal length in cm

- petal width in cm

- class:

- Iris-Setosa

- Iris-Versicolour

- Iris-Virginica

:Summary Statistics:

============== ==== ==== ======= ===== ====================

Min Max Mean SD Class Correlation

============== ==== ==== ======= ===== ====================

sepal length: 4.3 7.9 5.84 0.83 0.7826

sepal width: 2.0 4.4 3.05 0.43 -0.4194

petal length: 1.0 6.9 3.76 1.76 0.9490 (high!)

petal width: 0.1 2.5 1.20 0.76 0.9565 (high!)

============== ==== ==== ======= ===== ====================

:Missing Attribute Values: None

:Class Distribution: 33.3% for each of 3 classes.

:Creator: R.A. Fisher

:Donor: Michael Marshall (MARSHALL%PLU@io.arc.nasa.gov)

:Date: July, 1988

The famous Iris database, first used by Sir R.A. Fisher. The dataset is taken

from Fisher's paper. Note that it's the same as in R, but not as in the UCI

Machine Learning Repository, which has two wrong data points.

This is perhaps the best known database to be found in the

pattern recognition literature. Fisher's paper is a classic in the field and

is referenced frequently to this day. (See Duda & Hart, for example.) The

data set contains 3 classes of 50 instances each, where each class refers to a

type of iris plant. One class is linearly separable from the other 2; the

latter are NOT linearly separable from each other.

.. topic:: References

- Fisher, R.A. "The use of multiple measurements in taxonomic problems"

Annual Eugenics, 7, Part II, 179-188 (1936); also in "Contributions to

Mathematical Statistics" (John Wiley, NY, 1950).

- Duda, R.O., & Hart, P.E. (1973) Pattern Classification and Scene Analysis.

(Q327.D83) John Wiley & Sons. ISBN 0-471-22361-1. See page 218.

- Dasarathy, B.V. (1980) "Nosing Around the Neighborhood: A New System

Structure and Classification Rule for Recognition in Partially Exposed

Environments". IEEE Transactions on Pattern Analysis and Machine

Intelligence, Vol. PAMI-2, No. 1, 67-71.

- Gates, G.W. (1972) "The Reduced Nearest Neighbor Rule". IEEE Transactions

on Information Theory, May 1972, 431-433.

- See also: 1988 MLC Proceedings, 54-64. Cheeseman et al"s AUTOCLASS II

conceptual clustering system finds 3 classes in the data.

- Many, many more ...

データの利用

データの取得方法

irisデータセットから各データを取り出すのに、以下の2つの方法がある。

辞書のキーを使って呼び出す（例：iris_dataset['DESCR']）
キーの文字列をプロパティーに指定する（例：iris_dataset.DESCR）

全レコードの特徴量データの取得

'data'から、150の個体に関する4つの特徴量が150行4列の2次元配列で得られる。4つの特徴量は’feature_names’の4つの特徴名に対応している。

from sklearn.datasets import load_iris

iris_data = load_iris()

X = iris_data['data']

print(X)

# [[5.1 3.5 1.4 0.2]
#  [4.9 3.  1.4 0.2]
#  [4.7 3.2 1.3 0.2]
#  .....
#  [6.5 3.  5.2 2. ]
#  [6.2 3.4 5.4 2.3]
#  [5.9 3.  5.1 1.8]]

from sklearn.datasets import load_iris

iris_data = load_iris()

X = iris_data['data']

print(X)

# [[5.1 3.5 1.4 0.2]

# [4.9 3. 1.4 0.2]

# [4.7 3.2 1.3 0.2]

# .....

# [6.5 3. 5.2 2. ]

# [6.2 3.4 5.4 2.3]

# [5.9 3. 5.1 1.8]]

特定の特徴量のデータのみ取得

特定の特徴量に関する全個体のデータを取り出すときにはX[:, n]の形で指定する。

from sklearn.datasets import load_iris

iris_data = load_iris()

features = iris_data['feature_names']
X = iris_data['data']
n_feature = 2

feature = X[:, n_feature]

print("feature name : {}".format(features[n_feature]))
print("feature data :\n{}".format(feature))

# feature name : petal length (cm)
# feature data :
# [1.4 1.4 1.3 1.5 1.4 1.7 1.4 1.5 1.4 1.5 1.5 1.6 1.4 1.1 1.2 1.5 1.3 1.4
#  .....
#  5.7 5.2 5.  5.2 5.4 5.1]

from sklearn.datasets import load_iris

iris_data = load_iris()

features = iris_data['feature_names']

X = iris_data['data']

n_feature = 2

feature = X[:, n_feature]

print("feature name : {}".format(features[n_feature]))

print("feature data :\n{}".format(feature))

# feature name : petal length (cm)

# feature data :

# [1.4 1.4 1.3 1.5 1.4 1.7 1.4 1.5 1.4 1.5 1.5 1.6 1.4 1.1 1.2 1.5 1.3 1.4

# .....

# 5.7 5.2 5. 5.2 5.4 5.1]

特定のクラスのデータのみ抽出

特定のクラス（この場合は種類）のレコードのみを抽出する方法。ndarrayの条件による要素抽出を使う。

from sklearn.datasets import load_iris

iris_data = load_iris()

targets = iris_data['target_names']
features = iris_data['feature_names']
X = iris_data['data']
y = iris_data['target']

n_class = 1
data_1 = X[y==1]

print("data for class {}:\n{}".format(targets[n_class], X[y==n_class]))

# data for class versicolor:
# [[7.  3.2 4.7 1.4]
#  [6.4 3.2 4.5 1.5]
#  [6.9 3.1 4.9 1.5]
#  .....
#  [6.2 2.9 4.3 1.3]
#  [5.1 2.5 3.  1.1]
#  [5.7 2.8 4.1 1.3]]

from sklearn.datasets import load_iris

iris_data = load_iris()

targets = iris_data['target_names']

features = iris_data['feature_names']

X = iris_data['data']

y = iris_data['target']

n_class = 1

data_1 = X[y==1]

print("data for class {}:\n{}".format(targets[n_class], X[y==n_class]))

# data for class versicolor:

# [[7. 3.2 4.7 1.4]

# [6.4 3.2 4.5 1.5]

# [6.9 3.1 4.9 1.5]

# .....

# [6.2 2.9 4.3 1.3]

# [5.1 2.5 3. 1.1]

# [5.7 2.8 4.1 1.3]]

2次元で配置されたAxesを一括で扱う

2020-03-08 / tau / コメントする

subplots()やadd_subplot()で複数の行数・列数のAxesを生成すると、Axesオブジェクトの2次元の配列となる。

この結果に対して一律に処理をしたい場合（たとえば軸の値や凡例を設定したい、アスペクトを揃えたいなどの場合）、いちいち二重ループを回すのが面倒。

import numpy as np
import matplotlib.pyplot as plt

fig, axs = plt.subplots(2, 2)

x = np.linspace(-np.pi, np.pi)
n = 1
for row in axs:
    for ax in row:
        ax.plot(x, np.sin(n*x), label="n={}".format(n))
        n += 1
        ax.set_ylim(-1.2, 1.8)
        ax.legend(loc='upper left')

plt.show()

import numpy as np

import matplotlib.pyplot as plt

fig, axs = plt.subplots(2, 2)

x = np.linspace(-np.pi, np.pi)

n = 1

for row in axs:

for ax in row:

ax.plot(x, np.sin(n*x), label="n={}".format(n))

n += 1

ax.set_ylim(-1.2, 1.8)

ax.legend(loc='upper left')

plt.show()

これを1次元配列に変換して一括で扱う方法。

変換方法の1つは、以下のように1次元配列で取り出してしまう方法

axs_1d = [ax for row in axs for ax in row]

1	axs_1d = [ax for row in axs for ax in row]

あるいは、以下のように2次元配列を1次元に変換する方法（当初、reshape(1, -1)[0]のようなことをしていたが、reshape(-1)とすればよいことがわかった）。

axs_1d = axs.reshape(-1)

1	axs_1d = axs.reshape(-1)

こうすると1次元配列axs_1dで2次元のaxsの全要素に対してアクセス可能になる。

import numpy as np
import matplotlib.pyplot as plt

fig, axs = plt.subplots(2, 2)

axs_1d = axs.reshape(-1)

x = np.linspace(-np.pi, np.pi)
for n, ax in enumerate(axs_1d):
    ax.plot(x, np.sin(n*x), label="n={}".format(n))
    ax.set_ylim(-1.2, 1.8)
    ax.legend(loc='upper left')

plt.show()

import numpy as np

import matplotlib.pyplot as plt

fig, axs = plt.subplots(2, 2)

axs_1d = axs.reshape(-1)

x = np.linspace(-np.pi, np.pi)

for n, ax in enumerate(axs_1d):

ax.plot(x, np.sin(n*x), label="n={}".format(n))

ax.set_ylim(-1.2, 1.8)

ax.legend(loc='upper left')

plt.show()

このほかにflatten()、ravel()を使う方法もある。flatten()はコピーを返すが、Axesオブジェクトへの参照先は変わらないので同じ効果。

各グラフにカウンターの値を適用するときはenumerate、他のリストなどと同時に変えていくときはzipを使う。

matplotlib.pyplot.hist – ヒストグラム

2020-03-08 / tau / コメントする

概要

matplotlib.pyplot.histは、配列データのヒストグラムを描画する。主なパラメータのみ示す。

hist(X, bins, range, density, cumulative, histtype, rwidth, color, stacked): Xはヒストグラムのデータで一つのグラフに一つの1次元配列。その他のパラメーターは以下で説明。

ヒストグラムの形式

度数分布

1次元の配列でデータを渡すと、その度数分布が描かれる。

ただしデフォルトでは各ビンのエッジが区別できないため、これを描くためにはedghecolorの指定が必要。edgecolorの代わりにecで指定してもよい。

import numpy as np
import matplotlib.pyplot as plt

np.random.seed(0)

x = np.random.normal(0, 1, 100)

fig, axs = plt.subplots(1,2, figsize=(6.4, 2.4))

axs[0].hist(x)
axs[1].hist(x, edgecolor='k')

plt.show()

import numpy as np

import matplotlib.pyplot as plt

np.random.seed(0)

x = np.random.normal(0, 1, 100)

fig, axs = plt.subplots(1,2, figsize=(6.4, 2.4))

axs[0].hist(x)

axs[1].hist(x, edgecolor='k')

plt.show()

頻度分布

density=Trueを指定すると、頻度分布になる。各ビンの総和が1となるように調整され、形状は度数分布と同じ。

import numpy as np
import matplotlib.pyplot as plt

np.random.seed(0)

x = np.random.normal(0, 1, 100)

fig, axs = plt.subplots(1,2, figsize=(6.4, 2.4))

axs[0].hist(x, ec='k')
axs[1].hist(x, density=True, ec='k')

plt.show()

import numpy as np

import matplotlib.pyplot as plt

np.random.seed(0)

x = np.random.normal(0, 1, 100)

fig, axs = plt.subplots(1,2, figsize=(6.4, 2.4))

axs[0].hist(x, ec='k')

axs[1].hist(x, density=True, ec='k')

plt.show()

累積分布図

cumulative=Trueを指定すると、累積度数分布、累積頻度分布を描く。

import numpy as np
import matplotlib.pyplot as plt

np.random.seed(0)

x = np.random.normal(0, 1, 100)

fig, axs = plt.subplots(1,2, figsize=(6.4, 2.4))

axs[0].hist(x, cumulative=True, ec='k')
axs[1].hist(x, cumulative=True, density=True, ec='k')

plt.show()

import numpy as np

import matplotlib.pyplot as plt

np.random.seed(0)

x = np.random.normal(0, 1, 100)

fig, axs = plt.subplots(1,2, figsize=(6.4, 2.4))

axs[0].hist(x, cumulative=True, ec='k')

axs[1].hist(x, cumulative=True, density=True, ec='k')

plt.show()

ビン数

binsでヒストグラムの柱（ビン）の数等を指定する。デフォルトはbins=10。

bins=n: ビンの数を数値で指定する。
bins=sequence: ビンの境界値をリスト等で指定する。

ビン(bin)は英語で、店の商品や工場の部品などを入れておく大きなケース、ストッカーのことをいい、British Englishではごみ箱を指す。日本語の瓶(びん)の呼び名とは関係ないらしい。

import numpy as np
import matplotlib.pyplot as plt

np.random.seed(0)

x = np.random.normal(0, 1, 100)

fig, axs = plt.subplots(1, 2, figsize=(6.4, 2.4))

axs[0].hist(x, bins=5, ec='k')
axs[1].hist(x, bins=[-3, -2, -1, 0, 0.5, 1, 1.5, 2], ec='k')

plt.show()

import numpy as np

import matplotlib.pyplot as plt

np.random.seed(0)

x = np.random.normal(0, 1, 100)

fig, axs = plt.subplots(1, 2, figsize=(6.4, 2.4))

axs[0].hist(x, bins=5, ec='k')

axs[1].hist(x, bins=[-3, -2, -1, 0, 0.5, 1, 1.5, 2], ec='k')

plt.show()

レンジ

rangeでヒストグラムのビンを分割する範囲を指定する。そのレンジの上下限値の間でbinsで指定されたビンに分割される。

import numpy as np
import matplotlib.pyplot as plt

np.random.seed(0)

x = np.random.normal(0, 1, 100)

fig, axs = plt.subplots(1, 3, figsize=(9.6, 2.4))

axs[0].hist(x, edgecolor='k')
axs[1].hist(x, range=(-3, 3), ec='k')
axs[2].hist(x, range=(-1.5, 1.5), ec='k')

for ax in axs:
    ax.set_xlim(-3, 3)
    ax.set_xticks(np.arange(-3, 4, 1))

plt.show()

import numpy as np

import matplotlib.pyplot as plt

np.random.seed(0)

x = np.random.normal(0, 1, 100)

fig, axs = plt.subplots(1, 3, figsize=(9.6, 2.4))

axs[0].hist(x, edgecolor='k')

axs[1].hist(x, range=(-3, 3), ec='k')

axs[2].hist(x, range=(-1.5, 1.5), ec='k')

for ax in axs:

ax.set_xlim(-3, 3)

ax.set_xticks(np.arange(-3, 4, 1))

plt.show()

色・エッジの指定

colorでビンの色、edgecolor/ecでエッジの色、linewidthでエッジの幅を指定する。

import numpy as np
import matplotlib.pyplot as plt

np.random.seed(0)

x = np.random.normal(0, 1, 100)

fig, axs = plt.subplots(1, 2, figsize=(6.4, 2.4))

axs[0].hist(x, color='lightseagreen', edgecolor='k')
axs[1].hist(x, color='lightcoral', ec='navy', linewidth=3)

plt.show()

import numpy as np

import matplotlib.pyplot as plt

np.random.seed(0)

x = np.random.normal(0, 1, 100)

fig, axs = plt.subplots(1, 2, figsize=(6.4, 2.4))

axs[0].hist(x, color='lightseagreen', edgecolor='k')

axs[1].hist(x, color='lightcoral', ec='navy', linewidth=3)

plt.show()

ビンの幅

rwidthでビンの幅を指定する。デフォルトはrwidth=1で各ビンが密着。

import numpy as np
import matplotlib.pyplot as plt

np.random.seed(0)

x = np.random.normal(0, 1, 100)

fig, axs = plt.subplots(1, 2, figsize=(6.4, 2.4))

axs[0].hist(x, rwidth=0.8, ec='k')
axs[1].hist(x, bins=13, width=1.2, ec='k')

plt.show()

import numpy as np

import matplotlib.pyplot as plt

np.random.seed(0)

x = np.random.normal(0, 1, 100)

fig, axs = plt.subplots(1, 2, figsize=(6.4, 2.4))

axs[0].hist(x, rwidth=0.8, ec='k')

axs[1].hist(x, bins=13, width=1.2, ec='k')

plt.show()

ヒストグラムのタイプ

histtype='type'でヒストグラムのタイプを指定する。

bar: 一般的なヒストグラムの形状。
barstacked: 複数のヒストグラムの場合に、同じビンの値を積み上げていく。
step: ビンの間の境界を描かない。
stepfilled: ビンの間の境界を描かず、中を塗りつぶす。

以下の例では、'bar'、'step'、'stepfilled'について例示。

import numpy as np
import matplotlib.pyplot as plt

np.random.seed(0)

x = np.random.normal(0, 1, 100)

fig, axs = plt.subplots(1, 3, figsize=(9.6, 2.4))

axs[0].hist(x, histtype='bar', ec='k')
axs[1].hist(x, histtype='step', ec='k')
axs[2].hist(x, histtype='stepfilled', ec='k')

plt.show()

import numpy as np

import matplotlib.pyplot as plt

np.random.seed(0)

x = np.random.normal(0, 1, 100)

fig, axs = plt.subplots(1, 3, figsize=(9.6, 2.4))

axs[0].hist(x, histtype='bar', ec='k')

axs[1].hist(x, histtype='step', ec='k')

axs[2].hist(x, histtype='stepfilled', ec='k')

plt.show()

複数のヒストグラム

単純な重ね合わせ

複数のヒストグラムを重ね合わせるには、同じターゲットに対して各データについてhistを実行する。

単に重ね合わせると、初めの方のヒストグラムが後の方で塗りつぶされてしまうので、それらを見えるようにするにはalphaで透明度を指定する。

ただし単に重ね合わせただけの場合、各ヒストグラムのビンの境界が必ずしも一致しない。

import numpy as np
import matplotlib.pyplot as plt

np.random.seed(0)

x1 = np.random.normal(-2, 1, 500)
x2 = np.random.normal(0, 1, 500)
x3 = np.random.normal(2, 1, 500)

fig, axs = plt.subplots(1,2, figsize=(6.4, 2.4))

axs[0].hist(x1, color='c', edgecolor='k')
axs[0].hist(x2, color='m', edgecolor='k')
axs[0].hist(x3, color='g', edgecolor='k')

axs[1].hist(x1, color='c', edgecolor='k', alpha=0.5)
axs[1].hist(x2, color='m', edgecolor='k', alpha=0.5)
axs[1].hist(x3, color='g', edgecolor='k', alpha=0.5)

plt.show()

import numpy as np

import matplotlib.pyplot as plt

np.random.seed(0)

x1 = np.random.normal(-2, 1, 500)

x2 = np.random.normal(0, 1, 500)

x3 = np.random.normal(2, 1, 500)

fig, axs = plt.subplots(1,2, figsize=(6.4, 2.4))

axs[0].hist(x1, color='c', edgecolor='k')

axs[0].hist(x2, color='m', edgecolor='k')

axs[0].hist(x3, color='g', edgecolor='k')

axs[1].hist(x1, color='c', edgecolor='k', alpha=0.5)

axs[1].hist(x2, color='m', edgecolor='k', alpha=0.5)

axs[1].hist(x3, color='g', edgecolor='k', alpha=0.5)

plt.show()

ヒストグラムとplotの重ね合わせ

こちらを参照。

ビン境界の整合

複数のヒストグラムのビンの境界を一致させるには以下の方法がある。

各グラフに対して同じrangeとbins=nを指定する
各グラフに対して同じbins=sequenceを指定する

import numpy as np
import matplotlib.pyplot as plt

np.random.seed(0)

x1 = np.random.normal(-2, 1, 500)
x2 = np.random.normal(0, 1, 500)
x3 = np.random.normal(2, 1, 500)

fig, axs = plt.subplots(1,2, figsize=(6.4, 2.4))

axs[0].hist(x1, range=(-4, 4), bins=20, color='c', ec='k', alpha=0.5)
axs[0].hist(x2, range=(-4, 4), bins=20, color='m', ec='k', alpha=0.5)
axs[0].hist(x3, range=(-4, 4), bins=20, color='g', ec='k', alpha=0.5)

bn = np.linspace(-4, 4, 21)
axs[1].hist(x1, bins=bn, color='c', ec='k', alpha=0.5)
axs[1].hist(x2, bins=bn, color='m', ec='k', alpha=0.5)
axs[1].hist(x3, bins=bn, color='g', ec='k', alpha=0.5)

plt.show()

import numpy as np

import matplotlib.pyplot as plt

np.random.seed(0)

x1 = np.random.normal(-2, 1, 500)

x2 = np.random.normal(0, 1, 500)

x3 = np.random.normal(2, 1, 500)

fig, axs = plt.subplots(1,2, figsize=(6.4, 2.4))

axs[0].hist(x1, range=(-4, 4), bins=20, color='c', ec='k', alpha=0.5)

axs[0].hist(x2, range=(-4, 4), bins=20, color='m', ec='k', alpha=0.5)

axs[0].hist(x3, range=(-4, 4), bins=20, color='g', ec='k', alpha=0.5)

bn = np.linspace(-4, 4, 21)

axs[1].hist(x1, bins=bn, color='c', ec='k', alpha=0.5)

axs[1].hist(x2, bins=bn, color='m', ec='k', alpha=0.5)

axs[1].hist(x3, bins=bn, color='g', ec='k', alpha=0.5)

plt.show()

並べる・積み上げる

複数のデータを配列とした場合（複数の1次元のデータを並べて2次元配列として与えた場合）、デフォルトでは各ビンが横に並べられる。

また、stacked=Trueあるいはhisttype='barstacked'を指定した場合、同じ階級のビンが積み上げられる。

import numpy as np
import matplotlib.pyplot as plt

np.random.seed(0)

x1 = np.random.normal(-2, 1, 500)
x2 = np.random.normal(0, 1, 500)
x3 = np.random.normal(2, 1, 500)
X = [x1, x2, x3]

fig, axs = plt.subplots(1,3, figsize=(9.6, 2.4))

axs[0].hist(X, bins=20, ec='k')
axs[1].hist(X, bins=20, stacked=True, ec='k')
axs[2].hist(X, bins=20, histtype='barstacked', ec='k')

plt.show()

import numpy as np

import matplotlib.pyplot as plt

np.random.seed(0)

x1 = np.random.normal(-2, 1, 500)

x2 = np.random.normal(0, 1, 500)

x3 = np.random.normal(2, 1, 500)

X = [x1, x2, x3]

fig, axs = plt.subplots(1,3, figsize=(9.6, 2.4))

axs[0].hist(X, bins=20, ec='k')

axs[1].hist(X, bins=20, stacked=True, ec='k')

axs[2].hist(X, bins=20, histtype='barstacked', ec='k')

plt.show()

戻り値

n: 各ビンの値(度数または頻度)
bins: 各ビンの境界値
patches: ヒストグラム描画に使われたpatcheオブジェクトのリスト

単一のヒストグラムの場合

以下の例では、nの結果として10個のビンの度数が得られている。

import numpy as np
import matplotlib.pyplot as plt

np.random.seed(0)

x = np.random.normal(0, 1, 100)

fig, ax = plt.subplots(1, 1, figsize=(6.4, 2.4))

n, bins, patches = ax.hist(x)

print(n)
print(bins)
print(patches)

plt.show()

# [0.02073508 0.10367541 0.14514557 0.26955606 0.35249639 0.37323147
#  0.33176131 0.2280859  0.14514557 0.10367541]
# [-2.55298982 -2.07071537 -1.58844093 -1.10616648 -0.62389204 -0.1416176
#   0.34065685  0.82293129  1.30520574  1.78748018  2.26975462]
# <a list of 10 Patch objects>

import numpy as np

import matplotlib.pyplot as plt

np.random.seed(0)

x = np.random.normal(0, 1, 100)

fig, ax = plt.subplots(1, 1, figsize=(6.4, 2.4))

n, bins, patches = ax.hist(x)

print(n)

print(bins)

print(patches)

plt.show()

# [0.02073508 0.10367541 0.14514557 0.26955606 0.35249639 0.37323147

# 0.33176131 0.2280859 0.14514557 0.10367541]

# [-2.55298982 -2.07071537 -1.58844093 -1.10616648 -0.62389204 -0.1416176

# 0.34065685 0.82293129 1.30520574 1.78748018 2.26975462]

# <a list of 10 Patch objects>

複数のヒストグラムの配列の場合

複数のデータを配列で与えた場合の戻り値。nが3つのデータごとの配列になっている。

import numpy as np
import matplotlib.pyplot as plt

np.random.seed(0)

x1 = np.random.normal(-2, 1, 500)
x2 = np.random.normal(0, 1, 500)
x3 = np.random.normal(2, 1, 500)
X = [x1, x2, x3]

fig, ax = plt.subplots(1,1, figsize=(3.2, 2.4))

n, bins, patches = ax.hist(X, bins=20, ec='k')

print(n)
print(bins)
print(patches)

plt.show()

# [array([ 6., 10., 34., 59., 98., 92., 87., 62., 24., 20.,  8.,  0.,  0.,
#         0.,  0.,  0.,  0.,  0.,  0.,  0.]), array([ 0.,  0.,  0.,  2.,  5., 12., 33., 64., 89., 99., 89., 55., 33.,
#        12.,  6.,  1.,  0.,  0.,  0.,  0.]), array([  0.,   0.,   0.,   0.,   0.,   0.,   0.,   2.,   2.,  11.,  27.,
#         54.,  89.,  89., 106.,  66.,  34.,  12.,   6.,   2.])]
# [-4.77259276 -4.27541438 -3.778236   -3.28105763 -2.78387925 -2.28670087
#  -1.7895225  -1.29234412 -0.79516574 -0.29798737  0.19919101  0.69636938
#   1.19354776  1.69072614  2.18790451  2.68508289  3.18226127  3.67943964
#   4.17661802  4.6737964   5.17097477]
# <a list of 3 Lists of Patches objects>

import numpy as np

import matplotlib.pyplot as plt

np.random.seed(0)

x1 = np.random.normal(-2, 1, 500)

x2 = np.random.normal(0, 1, 500)

x3 = np.random.normal(2, 1, 500)

X = [x1, x2, x3]

fig, ax = plt.subplots(1,1, figsize=(3.2, 2.4))

n, bins, patches = ax.hist(X, bins=20, ec='k')

print(n)

print(bins)

print(patches)

plt.show()

# [array([ 6., 10., 34., 59., 98., 92., 87., 62., 24., 20., 8., 0., 0.,

# 0., 0., 0., 0., 0., 0., 0.]), array([ 0., 0., 0., 2., 5., 12., 33., 64., 89., 99., 89., 55., 33.,

# 12., 6., 1., 0., 0., 0., 0.]), array([ 0., 0., 0., 0., 0., 0., 0., 2., 2., 11., 27.,

# 54., 89., 89., 106., 66., 34., 12., 6., 2.])]

# [-4.77259276 -4.27541438 -3.778236 -3.28105763 -2.78387925 -2.28670087

# -1.7895225 -1.29234412 -0.79516574 -0.29798737 0.19919101 0.69636938

# 1.19354776 1.69072614 2.18790451 2.68508289 3.18226127 3.67943964

# 4.17661802 4.6737964 5.17097477]

# <a list of 3 Lists of Patches objects>

二項分布

2020-03-01 / tau / コメントする

概要

ある試行において起こり得る事象が2通りしかない場合、このような試行をベルヌーイ試行(Bernoulli trial)という。たとえばコインを投げた時に表が出るか裏が出るか、くじ引きを引いたときに当たりが出るかはずれが出るか、など。

ベルヌーイ試行の2つの事象を確率変数 $X = 1, 0$ で表し、 $X = 1$ となる確率が $p$ であるとする。

(1) $\begin{alignat*}{1} P(X=1) &= p \\ P(X=0) &= 1-p \end{alignat*}$

このようなベルヌーイ試行を $n$ 回繰り返したとき、 $X=1$ が生じる回数の確率分布が二項分布(Binomial distribution)で、 $B(n, p)$ のように表示される。二項分布の例には以下のようなものがある。

コインの表／裏が出る確率が等しく1/2のとき、このコインを10回投げた時に表がでる回数の分布
打率3割の打者が4回打席に立って2安打以上打つ確率

確率分布

$n$ 回のベルヌーイ試行のうち、 $X=1$ が $k$ 回起こるケースは、 ${}_n \mathrm{C}_k$ 通りなので、二項分布の確率は以下のように表せる。

(2) $\begin{equation*} P(X=k ; p) = {}_n \mathrm{C}_k p^k (1-p)^{n-k} \end{equation*}$

全事象

$k=0~n$ の確率の和が全事象の確率であり、二項定理から、

(3) $\begin{equation*} \sum_{k=0}^n {}_n \mathrm{C}_k p^k (1-p)^{n-k} = (p + 1 - p)^n = 1 \end{equation*}$

平均と分散

二項分布 $B(n, p)$ の平均と分散は、以下のようになる。

(4) $\begin{alignat*}{1} E(X) &= np \\ V(X) &= np(1-p) \end{alignat*}$

この導出において興味深いテクニックが使われる。

二項分布の形

$n=20, p=0.3$ の二項分布のグラフをPythonで描くと以下のようになる。

import numpy as np
from scipy.stats import binom
from scipy.stats import norm
import matplotlib.pyplot as plt

np.random.seed(0)

n = 20
p = 0.3

min_k = 0
max_k = n

data = np.random.binomial(n, p, size=100)

k = np.arange(min_k, max_k + 1)
binom_pmf = binom.pmf(k, n, p)

fig = plt.figure()
ax = fig.add_subplot(111)

ax.plot(k, binom_pmf, label="binomial PMF")
ax.hist(data, bins=20, range=(min_k, max_k), density=True,
    color='c', edgecolor='k', label="binomial trials")
ax.legend(loc="upper right")
ax.text(15, 0.175, "n={}".format(n))
ax.text(15, 0.165, "p={}".format(p))

plt.show()

import numpy as np

from scipy.stats import binom

from scipy.stats import norm

import matplotlib.pyplot as plt

np.random.seed(0)

n = 20

p = 0.3

min_k = 0

max_k = n

data = np.random.binomial(n, p, size=100)

k = np.arange(min_k, max_k + 1)

binom_pmf = binom.pmf(k, n, p)

fig = plt.figure()

ax = fig.add_subplot(111)

ax.plot(k, binom_pmf, label="binomial PMF")

ax.hist(data, bins=20, range=(min_k, max_k), density=True,

color='c', edgecolor='k', label="binomial trials")

ax.legend(loc="upper right")

ax.text(15, 0.175, "n={}".format(n))

ax.text(15, 0.165, "p={}".format(p))

plt.show()

正規分布近似

二項分布 $B(n, p)$ は、 $np, np(1-p)$ が十分大きいとき(具体的には5より大きいとき)、平均 $np$ 、分散 $np(1-p)$ の正規分布で近似できる(ド・モアブル－ラプラスの定理)。

(5) $\begin{equation*} X \sim B(n, p) \rightarrow \frac{X - np}{\sqrt{np(1-p)}} \sim N=(0, 1) \end{equation*}$

これは、二項分布の1回の試行において成功する場合をX_i = 1、失敗する場合をX_i = 0として、成功回数 $\sum X_i$ の平均と分散がnp, np(1 − p)であることからわかる。

以下は、 $n, p$ の3つずつの組み合わせに対する、二項分布と正規分布の一致具合を比べたもの。表示範囲は、正規分布とみなしたときの $-3\sigma \sim 3\sigma$ に対応する範囲で設定している。

import numpy as np
from scipy.stats import binom
from scipy.stats import norm
import matplotlib.pyplot as plt

np.random.seed(0)

fig = plt.figure(figsize=(12, 9))
fig.subplots_adjust(hspace=0.3)

n_subplot = 0
for n in [10, 100, 1000]:
    for p in [0.15, 0.3, 0.5]:
        n_subplot += 1
        k = np.arange(0, n + 1)
        mu = n * p
        sig = np.sqrt(n * p * (1 - p))
        binom_pmf = binom.pmf(k, n, p)
        norm_pdf = norm.pdf(k, loc=mu, scale=sig)

        ax = fig.add_subplot(3, 3, n_subplot)
        ax.set_xlim(np.ceil(mu - 3*sig), np.floor(mu + 3*sig))
        ax.plot(k, binom_pmf, color='y', linewidth=7, label="binomial PMF")
        ax.plot(k, norm_pdf, color='k', linewidth=2, label="normal PDF")
        ax.legend(loc="lower center", fontsize=8)
        ax.set_title("n={}, p={:.2f}%".format(n, p))

plt.show()

import numpy as np

from scipy.stats import binom

from scipy.stats import norm

import matplotlib.pyplot as plt

np.random.seed(0)

fig = plt.figure(figsize=(12, 9))

fig.subplots_adjust(hspace=0.3)

n_subplot = 0

for n in [10, 100, 1000]:

for p in [0.15, 0.3, 0.5]:

n_subplot += 1

k = np.arange(0, n + 1)

mu = n * p

sig = np.sqrt(n * p * (1 - p))

binom_pmf = binom.pmf(k, n, p)

norm_pdf = norm.pdf(k, loc=mu, scale=sig)

ax = fig.add_subplot(3, 3, n_subplot)

ax.set_xlim(np.ceil(mu - 3*sig), np.floor(mu + 3*sig))

ax.plot(k, binom_pmf, color='y', linewidth=7, label="binomial PMF")

ax.plot(k, norm_pdf, color='k', linewidth=2, label="normal PDF")

ax.legend(loc="lower center", fontsize=8)

ax.set_title("n={}, p={:.2f}%".format(n, p))

plt.show()

母集団確率の最尤推定

二項分布の母集団確率の最尤推定量は $p=k/n$ である。

実用例

適用例

二項確率が与えられたときの、発生回数や個体数の予測。

当たりの確率がpの掛けの、掛け回数nと当たりの回数k
故障率pの部品について、n個の部品のうちの故障数k
罹患率pの病気について、n人のうちの罹患者数k
支持率pの政党に対して、n人のうちの支持者数k

分析例

上記と逆に、nサンプルから事象がk回発生したときの確率を推定。

尤度・最尤推定

2020-03-01 / tau / コメントする

コインの例

最尤推定法(maximum likelihood estimation)は確率分布 $f_D$ のパラメーター $\theta$ を、その母集団から得られたサンプルから推定する方法。

たとえば、表の出る確率が必ずしも1/2でないコインを50回投げた時、表が15回出たとすると、このコインの表が出る確率はいくらか、といった問題。20～30回くらいの間だと普通のコインで表／裏の確率は1/2かなと思うが、50回投げて表が15回しかでないとちょっと疑いたくなる。

ここで、表が出る確率を $p$ として、 $n$ 回の試行中表が $k$ 回出る確率は以下の通り。

(1) $\begin{equation*} P(k:n\,|\,p) = \binom{n}{k} p^k (1-p)^{n-k} \end{equation*}$

先の問題の結果について、母集団の確率をいくつか仮定して計算してみると

(2) $\begin{equation*} \begin{align} p &= 1/2 \quad \rightarrow \quad P(15:50\,|\,0.5) \approx 0.002 \\ p &= 1/3 \quad \rightarrow \quad P(15:50\,|\,0.3) \approx 0.107 \\ p &= 1/4 \quad \rightarrow \quad P(15:50\,|\,0.1) \approx 0.089 \end{align} \end{equation*}$

得られたサンプルの下では、少なくともぼ表が出る確率を1/2や1/4と考えるよりは、1/3と考えた方がこのサンプルのパターンが発生する確率が高い。

そこで、サンプルのパターンに対して母集団の確率を変化させてみると、以下のようになる。

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import binom

n = 50
k = 15
p = np.linspace(0, 1, 100)

fig, ax = plt.subplots(figsize=(4.8, 3.6))

ax.plot(p, binom.pmf(k, n, p), c='navy')
ax.plot((k/n, k/n), (0, binom.pmf(k, n, k/n)), c='gray', linestyle='dashed')

ax.set_xlim(0, 1)
ax.set_ylim(0, 0.15)
ax.set_xticks(np.arange(0, 1.1, 0.1))

plt.show()

import numpy as np

import matplotlib.pyplot as plt

from scipy.stats import binom

n = 50

k = 15

p = np.linspace(0, 1, 100)

fig, ax = plt.subplots(figsize=(4.8, 3.6))

ax.plot(p, binom.pmf(k, n, p), c='navy')

ax.plot((k/n, k/n), (0, binom.pmf(k, n, k/n)), c='gray', linestyle='dashed')

ax.set_xlim(0, 1)

ax.set_ylim(0, 0.15)

ax.set_xticks(np.arange(0, 1.1, 0.1))

plt.show()

グラフ上は、母集団確率が15/50=0.3のときにサンプルパターンの発生確率が最も高くなっている。

解析的に確率が最大となる母集団確率を求めるために、式(1)を $p$ で微分してゼロとなる点を求める。

(3) $\begin{gather*} \frac{d P(k:n\,|\,p)}{dp} = \binom{n}{k}\left(kp^{k-1} (1-p)^{n-k} - p^k (n-k)(1-p)^{n-k-1} \right) = 0 \\ p^{k-1} (1-p)^{n-k-1} \left( k (1-p) - (n-k) p \right) = 0 \\ p^{k-1} (1-p)^{n-k-1} \left( k - np \right) = 0 \end{gather*}$

上式の解は $p = 0, 1, k/n$ となるが、 $p=0, 1$ の場合は式(1)がゼロとなることから、確率が最大となるのは $p=k/n$ であることがわかる。

尤度関数と最尤法

母集団の確率分布を $f$ 、母集団のパラメータを $\theta$ 、得られたサンプルセットを $x_1, \ldots, x_n$ とすると、パラメーターが $\theta$ である確率は

(4) $\begin{equation*} Pr(x_1, \ldots, x_n \,|\, \theta) = f(x_1, \ldots, x_n \,|\, \theta) \end{equation*}$

このとき、パラメーター $\theta$ に関する尤度関数は以下のように定義される。

(5) $\begin{equation*} L(\theta) = f(x_1, \ldots, x_n \,|\, \theta) \end{equation*}$

通常、尤度関数が最大となるパラメーターを求めるためには対数尤度関数が用いられる。

(6) $\begin{equation*} \frac{d}{d \theta} \ln L(\theta) = 0 \end{equation*}$

サンプルの質と尤度

先のコインの問題で、試行数が10回の場合と100回の場合を比べてみる。それぞれについて、表の確率が0.3、0.5、0.7に対応する回数は試行回数が10回の場合は3回、5回、7回、試行回数100回に対しては30回、50回、70回である。それぞれの表の階数に対して、母集団確率の尤度関数を描くと以下のようになる。

import numpy as np
import matplotlib.pyplot as plt
from functools import reduce

def comb(n, k):
    numer = reduce(lambda x,y:x*y, range(n - k + 1, n))
    denom = reduce(lambda x,y:x*y, range(1, k + 1))
    return numer // denom

def binom(n, k, p):
    return comb(n, k) * p**k * (1 - p)**(n - k)

n = [10, 100]
k = [np.array([3, 5, 7]), np.array([30, 50, 70])]

p = np.linspace(0, 1, 100)

fig, axs = plt.subplots(1, 2, figsize=(9.6, 3.6))

for ax, n, k in zip(axs, n, k):
    ax.set_title("n={}".format(n))

    for t in k:
        p_mle = t / n
        prob = binom(n, t, p)

        ax.plot(p, prob, c='navy')
        ax.plot((p_mle, p_mle), (0, binom(n, t, p_mle)), c='gray', linestyle='dashed')

        ax.set_xlim(0, 1)
        ax.set_xticks(np.arange(0, 1.1, 0.1))

plt.show()

import numpy as np

import matplotlib.pyplot as plt

from functools import reduce

def comb(n, k):

numer = reduce(lambda x,y:x*y, range(n - k + 1, n))

denom = reduce(lambda x,y:x*y, range(1, k + 1))

return numer // denom

def binom(n, k, p):

return comb(n, k) * p**k * (1 - p)**(n - k)

n = [10, 100]

k = [np.array([3, 5, 7]), np.array([30, 50, 70])]

p = np.linspace(0, 1, 100)

fig, axs = plt.subplots(1, 2, figsize=(9.6, 3.6))

for ax, n, k in zip(axs, n, k):

ax.set_title("n={}".format(n))

for t in k:

p_mle = t / n

prob = binom(n, t, p)

ax.plot(p, prob, c='navy')

ax.plot((p_mle, p_mle), (0, binom(n, t, p_mle)), c='gray', linestyle='dashed')

ax.set_xlim(0, 1)

ax.set_xticks(np.arange(0, 1.1, 0.1))

plt.show()

試行回数が100回の場合には分布が尖っており、最尤推定されたパラメーターの確度が高いが、10回の場合には分布がなだらかで、最尤推定された値以外のパラメーターの確率も高くなっている。

最尤推定の場合、サンプルの規模が推定値の信頼度に関わってくる。

概要

特徴量の分布

クラス分けしない場合

クラス分けした場合

2つの特徴量同士の関係

比較例

scatter_matrixによる確認

pairplotによる確認

3つの特徴量の関係

概要

基本形

複数系列

概要

データの取得とデータ構造

データの内容

'data'～特徴量データセット

'target'～アヤメの種類に対応したコード

'target_names'～アヤメの種類名

'feature_names'～特徴名

'filename'～ファイル名

'DESCR'～データセットの説明

データの利用

データの取得方法

全レコードの特徴量データの取得

特定の特徴量のデータのみ取得

特定のクラスのデータのみ抽出

概要

ヒストグラムの形式

度数分布

頻度分布

累積分布図

ビン数

レンジ

色・エッジの指定

ビンの幅

ヒストグラムのタイプ

複数のヒストグラム

単純な重ね合わせ

ヒストグラムとplotの重ね合わせ

ビン境界の整合

並べる・積み上げる

戻り値

単一のヒストグラムの場合

複数のヒストグラムの配列の場合

概要

確率分布

全事象

平均と分散

二項分布の形

正規分布近似

母集団確率の最尤推定

実用例

適用例

分析例

コインの例

尤度関数と最尤法

サンプルの質と尤度

`scatter_matrix`による確認

`pairplot`による確認

`'data'`～特徴量データセット

`'target'`～アヤメの種類に対応したコード

`'target_names'`～アヤメの種類名

`'feature_names'`～特徴名

`'filename'`～ファイル名

`'DESCR'`～データセットの説明