コインの例
最尤推定法(maximum likelihood estimation)は確率分布![]() のパラメーター
のパラメーター![]() を、その母集団から得られたサンプルから推定する方法。
を、その母集団から得られたサンプルから推定する方法。
たとえば、表の出る確率が必ずしも1/2でないコインを50回投げた時、表が15回出たとすると、このコインの表が出る確率はいくらか、といった問題。20~30回くらいの間だと普通のコインで表/裏の確率は1/2かなと思うが、50回投げて表が15回しかでないとちょっと疑いたくなる。
ここで、表が出る確率を![]() として、
として、![]() 回の試行中表が
回の試行中表が![]() 回出る確率は以下の通り。
回出る確率は以下の通り。
(1) ![]()
先の問題の結果について、母集団の確率をいくつか仮定して計算してみると
(2) 
得られたサンプルの下では、少なくともぼ表が出る確率を1/2や1/4と考えるよりは、1/3と考えた方がこのサンプルのパターンが発生する確率が高い。
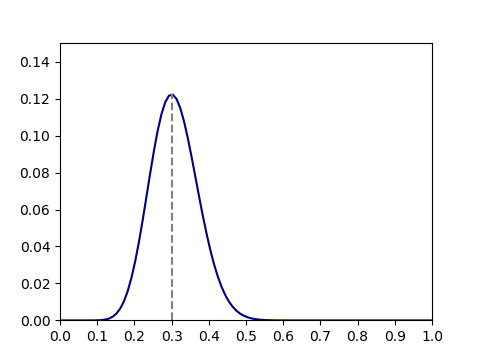
そこで、サンプルのパターンに対して母集団の確率を変化させてみると、以下のようになる。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
import numpy as np import matplotlib.pyplot as plt from scipy.stats import binom n = 50 k = 15 p = np.linspace(0, 1, 100) fig, ax = plt.subplots(figsize=(4.8, 3.6)) ax.plot(p, binom.pmf(k, n, p), c='navy') ax.plot((k/n, k/n), (0, binom.pmf(k, n, k/n)), c='gray', linestyle='dashed') ax.set_xlim(0, 1) ax.set_ylim(0, 0.15) ax.set_xticks(np.arange(0, 1.1, 0.1)) plt.show() |
グラフ上は、母集団確率が15/50=0.3のときにサンプルパターンの発生確率が最も高くなっている。
解析的に確率が最大となる母集団確率を求めるために、式(1)を![]() で微分してゼロとなる点を求める。
で微分してゼロとなる点を求める。
(3) 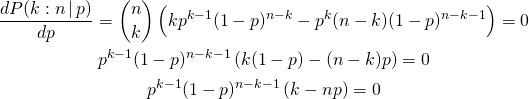
上式の解は![]() となるが、
となるが、![]() の場合は式(1)がゼロとなることから、確率が最大となるのは
の場合は式(1)がゼロとなることから、確率が最大となるのは![]() であることがわかる。
であることがわかる。
尤度関数と最尤法
母集団の確率分布を![]() 、母集団のパラメータを
、母集団のパラメータを![]() 、得られたサンプルセットを
、得られたサンプルセットを![]() とすると、パラメーターが
とすると、パラメーターが![]() である確率は
である確率は
(4) ![]()
このとき、パラメーター![]() に関する尤度関数は以下のように定義される。
に関する尤度関数は以下のように定義される。
(5) ![]()
通常、尤度関数が最大となるパラメーターを求めるためには対数尤度関数が用いられる。
(6) ![]()
サンプルの質と尤度
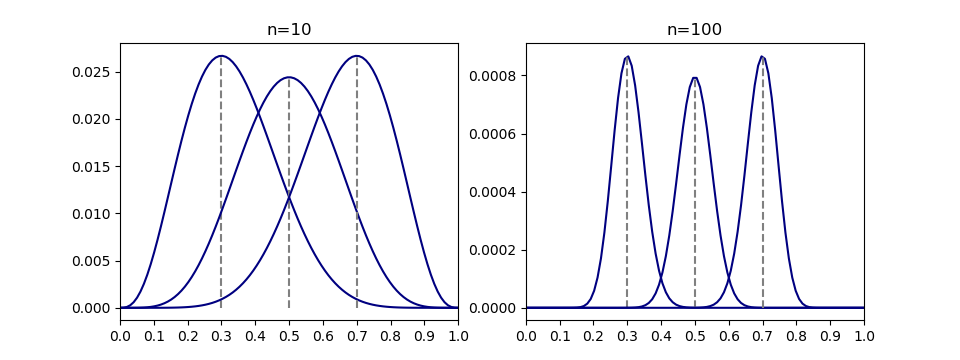
先のコインの問題で、試行数が10回の場合と100回の場合を比べてみる。それぞれについて、表の確率が0.3、0.5、0.7に対応する回数は試行回数が10回の場合は3回、5回、7回、試行回数100回に対しては30回、50回、70回である。それぞれの表の階数に対して、母集団確率の尤度関数を描くと以下のようになる。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 |
import numpy as np import matplotlib.pyplot as plt from functools import reduce def comb(n, k): numer = reduce(lambda x,y:x*y, range(n - k + 1, n)) denom = reduce(lambda x,y:x*y, range(1, k + 1)) return numer // denom def binom(n, k, p): return comb(n, k) * p**k * (1 - p)**(n - k) n = [10, 100] k = [np.array([3, 5, 7]), np.array([30, 50, 70])] p = np.linspace(0, 1, 100) fig, axs = plt.subplots(1, 2, figsize=(9.6, 3.6)) for ax, n, k in zip(axs, n, k): ax.set_title("n={}".format(n)) for t in k: p_mle = t / n prob = binom(n, t, p) ax.plot(p, prob, c='navy') ax.plot((p_mle, p_mle), (0, binom(n, t, p_mle)), c='gray', linestyle='dashed') ax.set_xlim(0, 1) ax.set_xticks(np.arange(0, 1.1, 0.1)) plt.show() |
試行回数が100回の場合には分布が尖っており、最尤推定されたパラメーターの確度が高いが、10回の場合には分布がなだらかで、最尤推定された値以外のパラメーターの確率も高くなっている。
最尤推定の場合、サンプルの規模が推定値の信頼度に関わってくる。