分散の定義
標本分散・母分散は、標本値や確率変数の平均からの偏差の自乗平均で定義される。
(1) 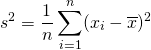
(2) 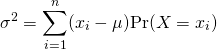
(3) ![]()
分散の定義の一般形は以下の通りで、母集団の確率分布によらない。
(4) ![]()
証明
(5) 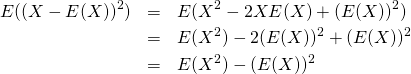
分散の性質
分散には以下の性質がある。
(6) ![]()
(7) ![]()
(8) ![]()
定数加算
標本値、確率変数に定数を加えても、分散の値は変わらない。これは、分散が各標本値・確率変数の平均からの偏差の平均であり、定数のバイアスはキャンセルアウトされることから明らかでもある。
![]()
証明
(9) 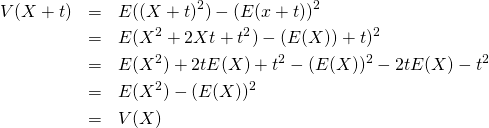
定数倍
標本値、確率変数を定数倍した場合、分散の値は定数の自乗倍になる。これは、分散の定義の形からも明らか。
![]()
証明
(10) 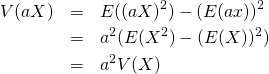
和の分散
2変数の場合
二つの標本値の組や確率変数を加えた場合の分散は、それぞれの分散の和に双方の共分散を加えた値になる。平均のような線形性がなく、2変数の和の2乗を展開した形と類似している。
![]()
証明
(11) 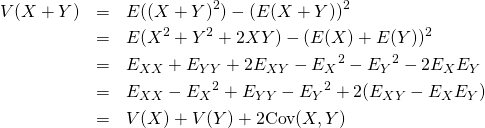
上式で![]() などと置き換えている。
などと置き換えている。
3変数の場合
3つ確率変数の和の場合は以下の通りで、3つの変数の和の2乗を展開した形と類似している。
(12) ![]()
証明
(13) 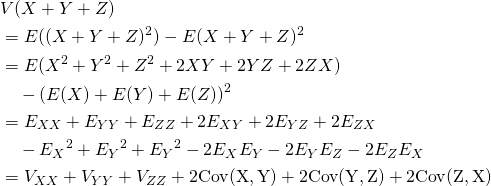
和の分散~独立な場合
確率変数![]() と
と![]() が独立なとき、次項で示すように共分散がゼロとなり、以下が成り立つ。
が独立なとき、次項で示すように共分散がゼロとなり、以下が成り立つ。
(14) ![]()
共分散の定義
2つの標本値、確率変数の共分散は以下で定義される。
(15) 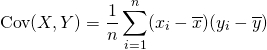
これは以下のようにも表現できる。
(16) ![]()
証明
(17) 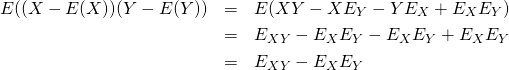
共分散は、2つの標本値、確率変数に正の相関が強い場合に生となり、負の相関が強い場合に負となる。また、相関が弱い場合にゼロに近くなる。
共分散の性質
定数加算
共分散の変数に定数を加えても、加える前の共分散と同じ値になる。定数をいずれの変数に加えても同じ。
(18) 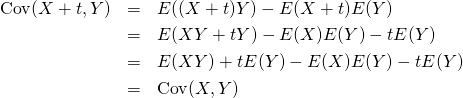
定数倍
共分散の変数を定数倍すると、もとの共分散の定数倍になる。両方の変数を定数倍すると、もとの共分散に双方の定数の積を乗じた値になる。
(19) 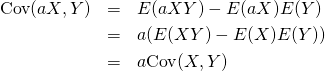
和の共分散
標本値、確率変数の和は、加える前の個々の共分散の和になる。すなわち、共分散においては分配法則が成り立つ。
(20) ![]()
証明
(21) 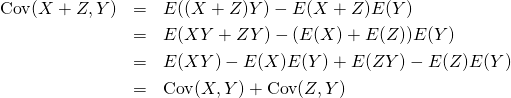
独立事象の共分散
2つの確率変数の事象が独立な場合、共分散はゼロとなる。
証明:離散型確率変数
![]() と
と![]() が独立ならば、その同時生起確率はそれぞれの確率の積となるので。
が独立ならば、その同時生起確率はそれぞれの確率の積となるので。
(22) ![]()
これより
(23) 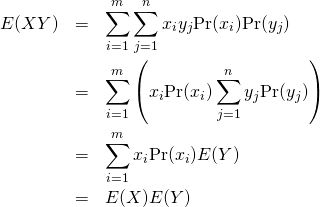
これを定義式に適用して![]() が確認できる。
が確認できる。
証明:連続型確率変数
![]() と
と![]() が独立なとき、その確率密度はそれぞれの確率密度の積となる。
が独立なとき、その確率密度はそれぞれの確率密度の積となる。
(24) ![]()
これより
(25) 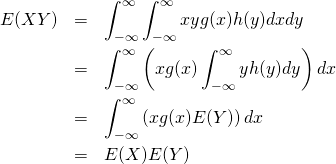
これを定義式に適用して![]() が確認できる。
が確認できる。
線形関係の場合の共分散
XとYが完全な線形関係にある場合の共分散は、XまたはY(いずれでもよい)の分散の定数倍になる。
証明
(26) 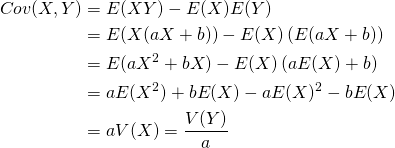
大学院試を控えている学部生の者です。非常に参考にさせて頂きました。
3変数の分散の計算のところにおいて、E[X]をExと表記するならば、Exx-Ex^2=Vxと書く方が表記に則っているように思えて、違和感がありました。
駄文失礼致しました。
ご指摘ありがとうございます。
仰る通りだと思います。
ちょっと前のものですが、共分散との並びで敢えてこう書きました。
たくさんの変数が出てくるような場合には、そもそもの変数の意味だとか計算過程ができるだけ直感で分かるように、自分の理解用の書き方を考えたりしています。
ここでは変数も少ないし他との並びからみてもきれいではないですね。