不偏推定量
標本平均の期待値、分散について考える。イメージとして、母集団からn個の標本値を取り出して期待値![]() を計算し、これを繰り返した場合の
を計算し、これを繰り返した場合の![]() の平均と分散を求めることになる。
の平均と分散を求めることになる。
まず、![]() の期待値については以下のように計算され、標本平均の期待値が母平均の不偏推定量であることがわかる。
の期待値については以下のように計算され、標本平均の期待値が母平均の不偏推定量であることがわかる。
(1) 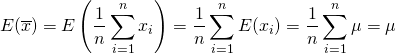
次に![]() の分散は以下のように計算される。
の分散は以下のように計算される。
(2) 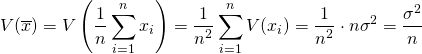
ここで、xiはそれぞれ独立に選ばれることから、V(x1, …, xn)は線形に分解できる。
標本平均![]() の分散がXの母分散をnで割った値となっているのは、標本平均を計算する項数が多いほど期待値に対する誤差が小さくなることを示唆している。
の分散がXの母分散をnで割った値となっているのは、標本平均を計算する項数が多いほど期待値に対する誤差が小さくなることを示唆している。
式(2)は、次のように偏差の自乗和の期待値でも表現できる。
(3) ![]()
確率分布
標本X1, …, Xnの母集団が正規分布N(μ, σ2)に従うとき、標本の和X1 + ··· + Xnは正規分布N(nμ, nσ2)に従い標本平均![]() はN(μ, σ2/n)に従うことが知られている。
はN(μ, σ2/n)に従うことが知られている。
また母集団の分布が正規分布でないとしても、中心極限定理により、標本の数(この場合は平均を取り出す回数)を多くすれば、その平均は正規分布に従う。
確率分布の解説のところで、
…標本平均X(bar)はN(μ, nσ2/n)に従うことが知られている。
とありますが、
N(μ, σ2/n)に従う
なのではないでしょうか。
当方の勘違いかもしれませんが、確認をお願いします。
ご指摘をいただいて感謝します。
恥ずかしながら私の誤記でした。
文字抜けも含めて修正いたしました。
ありがとうございました。