概要
ある試行において起こり得る事象が2通りしかない場合、このような試行をベルヌーイ試行(Bernoulli trial)という。たとえばコインを投げた時に表が出るか裏が出るか、くじ引きを引いたときに当たりが出るかはずれが出るか、など。
ベルヌーイ試行の2つの事象を確率変数![]() で表し、
で表し、![]() となる確率が
となる確率が![]() であるとする。
であるとする。
(1) ![]()
このようなベルヌーイ試行を![]() 回繰り返したとき、
回繰り返したとき、![]() が生じる回数の確率分布が二項分布(Binomial distribution)で、
が生じる回数の確率分布が二項分布(Binomial distribution)で、![]() のように表示される。二項分布の例には以下のようなものがある。
のように表示される。二項分布の例には以下のようなものがある。
- コインの表/裏が出る確率が等しく1/2のとき、このコインを10回投げた時に表がでる回数の分布
- 打率3割の打者が4回打席に立って2安打以上打つ確率
確率分布
![]() 回のベルヌーイ試行のうち、
回のベルヌーイ試行のうち、![]() が
が![]() 回起こるケースは、
回起こるケースは、![]() 通りなので、二項分布の確率は以下のように表せる。
通りなので、二項分布の確率は以下のように表せる。
(2) ![]()
全事象
![]() の確率の和が全事象の確率であり、二項定理から、
の確率の和が全事象の確率であり、二項定理から、
(3) 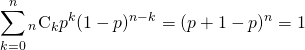
平均と分散
二項分布![]() の平均と分散は、以下のようになる。
の平均と分散は、以下のようになる。
(4) ![]()
二項分布の形
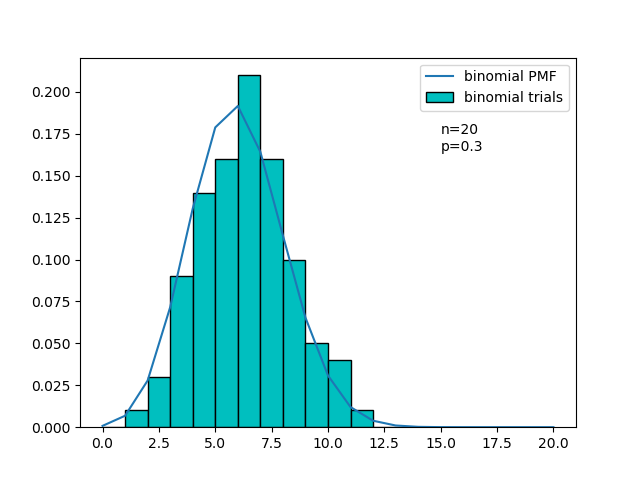
![]() の二項分布のグラフをPythonで描くと以下のようになる。
の二項分布のグラフをPythonで描くと以下のようになる。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 |
import numpy as np from scipy.stats import binom from scipy.stats import norm import matplotlib.pyplot as plt np.random.seed(0) n = 20 p = 0.3 min_k = 0 max_k = n data = np.random.binomial(n, p, size=100) k = np.arange(min_k, max_k + 1) binom_pmf = binom.pmf(k, n, p) fig = plt.figure() ax = fig.add_subplot(111) ax.plot(k, binom_pmf, label="binomial PMF") ax.hist(data, bins=20, range=(min_k, max_k), density=True, color='c', edgecolor='k', label="binomial trials") ax.legend(loc="upper right") ax.text(15, 0.175, "n={}".format(n)) ax.text(15, 0.165, "p={}".format(p)) plt.show() |
正規分布近似
二項分布![]() は、
は、![]() が十分大きいとき(具体的には5より大きいとき)、平均
が十分大きいとき(具体的には5より大きいとき)、平均![]() 、分散
、分散![]() の正規分布で近似できる(ド・モアブル-ラプラスの定理)。
の正規分布で近似できる(ド・モアブル-ラプラスの定理)。
(5) ![]()
これは、二項分布の1回の試行において成功する場合をXi = 1、失敗する場合をXi = 0として、成功回数![]() の平均と分散がnp, np(1 − p)であることからわかる。
の平均と分散がnp, np(1 − p)であることからわかる。
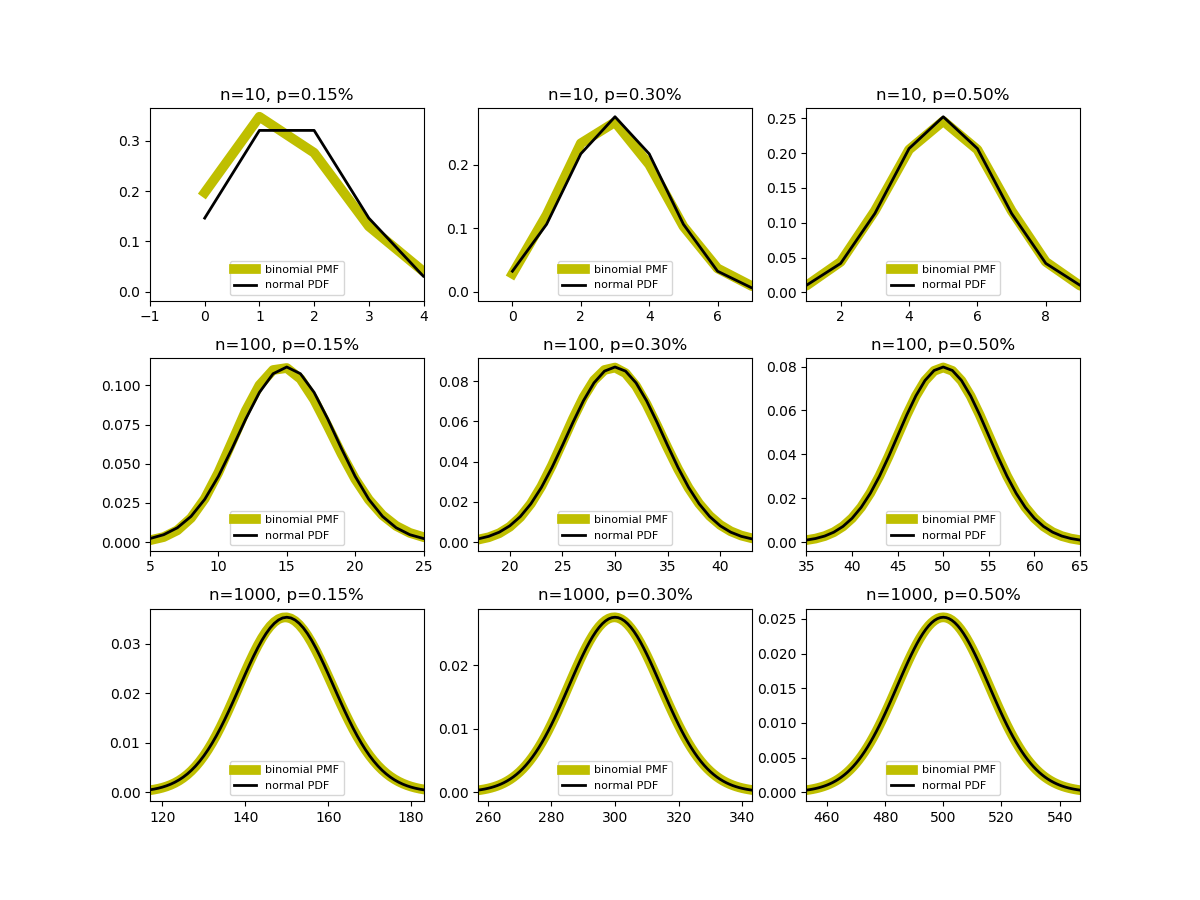
以下は、![]() の3つずつの組み合わせに対する、二項分布と正規分布の一致具合を比べたもの。表示範囲は、正規分布とみなしたときの
の3つずつの組み合わせに対する、二項分布と正規分布の一致具合を比べたもの。表示範囲は、正規分布とみなしたときの![]() に対応する範囲で設定している。
に対応する範囲で設定している。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 |
import numpy as np from scipy.stats import binom from scipy.stats import norm import matplotlib.pyplot as plt np.random.seed(0) fig = plt.figure(figsize=(12, 9)) fig.subplots_adjust(hspace=0.3) n_subplot = 0 for n in [10, 100, 1000]: for p in [0.15, 0.3, 0.5]: n_subplot += 1 k = np.arange(0, n + 1) mu = n * p sig = np.sqrt(n * p * (1 - p)) binom_pmf = binom.pmf(k, n, p) norm_pdf = norm.pdf(k, loc=mu, scale=sig) ax = fig.add_subplot(3, 3, n_subplot) ax.set_xlim(np.ceil(mu - 3*sig), np.floor(mu + 3*sig)) ax.plot(k, binom_pmf, color='y', linewidth=7, label="binomial PMF") ax.plot(k, norm_pdf, color='k', linewidth=2, label="normal PDF") ax.legend(loc="lower center", fontsize=8) ax.set_title("n={}, p={:.2f}%".format(n, p)) plt.show() |
母集団確率の最尤推定
二項分布の母集団確率の最尤推定量は![]() である。
である。
実用例
適用例
二項確率が与えられたときの、発生回数や個体数の予測。
- 当たりの確率がpの掛けの、掛け回数nと当たりの回数k
- 故障率pの部品について、n個の部品のうちの故障数k
- 罹患率pの病気について、n人のうちの罹患者数k
- 支持率pの政党に対して、n人のうちの支持者数k
分析例
上記と逆に、nサンプルから事象がk回発生したときの確率を推定。