概要
matplotlib.pyplot.quiver()はベクトル場を可視化する。基本的なパラメーターは以下の通り。
quiver(X, Y, U, V, [C])X, Yはベクトルの開始点、U, Vはベクトルの成分、Cはベクトルの大きさに応じたカラーマップ上の色をつけるための配列。
単一のベクトルの描画例
以下の例では、始点の位置と成分を1つずつ指定してベクトルを描画している。デフォルトではベクトルのスケールは描画領域に対して自動的に調節されるが、ここでは描画領域のスケールと同じになるようパラメーターを設定している。
matplotlibのドキュメントでは、scale_unitsのところに以下のように書かれている。
“To plot vectors in the x-y plane, with u and v having the same units as x and y, use angles='xy', scale_units='xy', scale=1”
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
import numpy as np import matplotlib.pyplot as plt fig, ax = plt.subplots() ax.quiver(1, 2, color='blue', angles='xy', scale_units='xy', scale=1) ax.quiver(1, 2, 2, -1, color='red', angles='xy', scale_units='xy', scale=1) ax.set_xlim(0, 3) ax.set_ylim(0, 3) ax.set_xticks(np.arange(0, 4, 1)) ax.set_yticks(np.arange(0, 4, 1)) ax.grid() ax.set_aspect('equal') plt.show() |
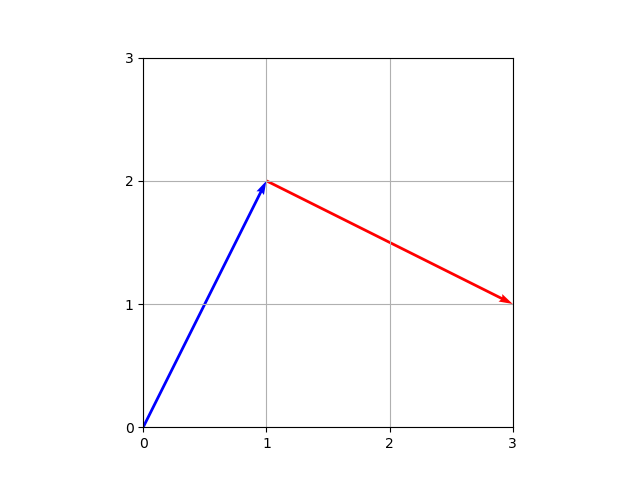
ベクトル場の描画例
以下の例では、xy平面上の位置に応じた成分を持つベクトルを描画している。関数のgradientのイメージ。
描画にあたって、開始点の座標とベクトルの成分をmeshgridで生成している。
1つ目の図は単に開始点と成分を与えただけで、単一の色で、ベクトルのスケールは自動調節されている。
2つ目の図はスケールと色付けのための配列を指定し、ベクトルの大きさに応じてcolormapで色を付けている。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 |
import numpy as np import matplotlib.pyplot as plt x = y = np.arange(-5, 6) u = 2 * x v = 3 * y x, y = np.meshgrid(x, y) u, v = np.meshgrid(u, v) fig, axes = plt.subplots(1, 2, figsize=(12, 4.8)) lim = 8 for ax in axes: ax.set_xlim(-lim, lim) ax.set_ylim(-lim, lim) ax.set_xticks(np.arange(-lim, lim, 1)) ax.set_yticks(np.arange(-lim, lim, 1)) ax.grid() ax.set_aspect('equal') C = np.sqrt(u * u + v * v) axes[0].quiver(x, y, u, v) axes[1].quiver(x, y, u, v, C, scale=100, cmap='Blues') plt.show() |
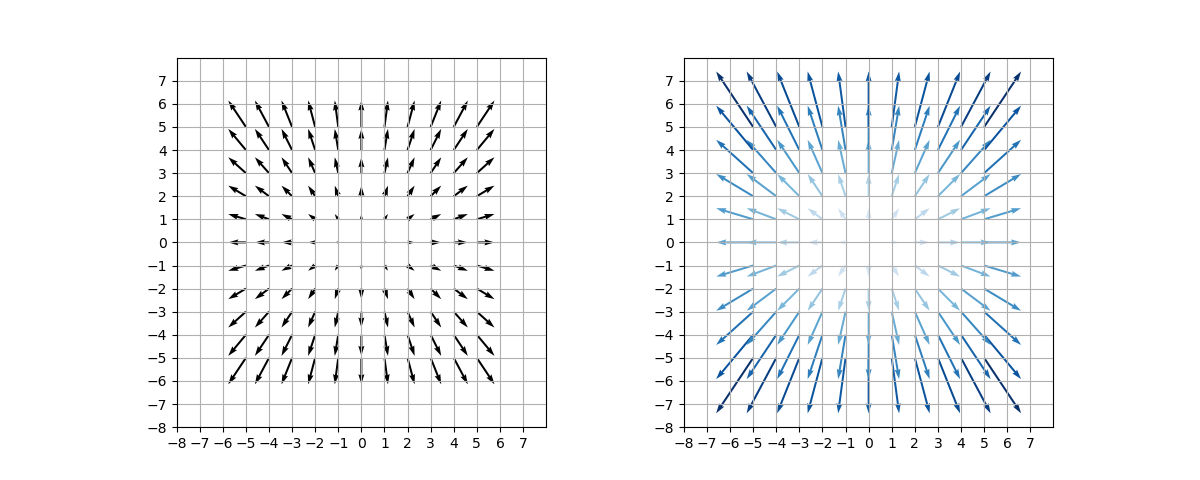
コメント失礼します。
わかりやすい解説とても参考にさせて戴いております。
こちら、プログラミング初心者です。
現在プログラミングを大学で教わっているのですが、2次元平面に(0,0)を始点に乱数ベクトルを2つプロットし、できるならグラムシュミット直交化せよ。という課題があり、こちらのコードをサンプルにさせていただいて乱数ベクトルをプロットさせることはできたのですが直交化がうまくいかなくて悩んでおります。よろしければアドバイスなどいただいてもよろしいでしょうか?
コメントありがとうございます。
グラムシュミット直行化というのは不勉強で存じませんでした。
勉強になりました。
ネットで調べてみると、線形独立なベクトル群から正規直行基底のベクトル群を作り出す方法のようですね。
2次元の場合の手順はこんな感じでしょうか。
(1) 2つのベクトルa1, a2のうち1つ、たとえばa1を選んで正規化(長さ1にする)。
u1 = a1 / |a1|
(2-1) 2つ目のベクトルa2からu1(a1)に平行な成分を除く。結果はa2の方向からu1(a1)の成分のみがない(つまりu1(a1)に直交した)ベクトルに変形される。
v2 = (a2・u1)u1
(2-2) 得られたv2を正規化
u2 = v1 / |v2|
この(u1, u2)が正規直行基底になります。
Pythonの場合はimport mathとしておいて、ベクトルa1 = (a1x, a1y)とすると、
|a1| = sqrt(a1x * a1 + a1y * a1y)
u1 = (u1x, u1y) = (u1x / |a1|, u1y / |a1|)
・・・
といった手順でしょうか。
内積a2・u1は各要素の積の和で計算ですね。
念には念を入れるなら、乱数で生成した2つのベクトルが線形独立かどうかのチェックはお好みで。
この際、ベクトルのクラスを定義して絶対値や内積計算を実装してもいいし、numpyを使うと配列をベクトルとみなして内積や絶対値(norm)を計算する関数が用意されているようです。
課題の趣旨によって、ライブラリーを使うか、計算の内容も問われているなら地道にコードを書くか選択されるとよいのでは。
それから目的によりますが、quiverはメッシュ状の多数のベクトルの分布を描くものなので、簡単に2次元のベクトルを描くだけならplotだけでもいいかもしれないですね。
課題頑張ってください。
わざわざ調べていただいてお手数おかけしました。
ありがとうございます。
参考とさせていただきます。