概要
scikit-learnの主成分分析モデル(PCA)をBiston housing pricesデータに適用して、その挙動を確認する。
主成分が適切に発見されてよい相関が得られることを期待したが、IrisデータやBreast cancerデータの場合のようなクラス分類データにおける良好な結果は得られなかった。
ただし、Boston housing pricesデータはIrisやcancerのデータよりも複雑な社会行動に関するものであり、その指標も限定されていることから、これをもってPCAが回帰系のデータに不向きとまでは言い切れない。
なお、Boston housing pricesデータの特徴量には属性データ(カテゴリーデータ、クラスデータ)が含まれることから、DataFrameのget_dummis()メソッドによるone-hot encodingを行っている。
計算の手順
- 必要なパッケージをインポート
- Boston housing pricesデータセットを準備
- データセットをスケーリング/エンコーディング
- 属性データの列を取り出して、get_dummiesでone-hot化
StandardScalerで残りの特徴量データを標準化- 上記2つを結合して前処理済みデータとして準備
- PCAモデルのインスタンスを生成
- 引数
n_components=2として、2つの特徴量について計算
- 引数
fit()メソッドにより、モデルにデータを学習させる- 主成分やその寄与率を確認
- 主成分は
PCA.comonents_を、寄与率はPCA.explained_variance_ratio_を確認
- 主成分は
transform()メソッドによって、主成分に沿ってデータを変換- 3つの主成分について3次元可視化
- 2つの主成分について2次元可視化
前処理
特徴量のうちの1つCHASについては、「チャールズ川に関するダミー変数(1:川沿い、0:それ以外)」~”Charles River dummy variable (= 1 if tract bounds river; 0 otherwise)“となっていて、0か1の属性変数である。この変数をDataFrameのget_dummies()メソッドでone-hot化する。
また、その他のデータについてはStandardScalerで標準化する。
CHASのデータのみone-hot化CHASの列を除いたデータをStandardScalerで標準化- 上記2つのデータを
join()で結合
|
1 2 3 4 5 |
df_chas_encoded = pd.get_dummies(df['CHAS'], prefix='CHAS') df_wo_chas = df.drop('CHAS', axis=1) df_wo_chas_scaled = pd.DataFrame( StandardScaler().fit_transform(df_wo_chas), columns=df_wo_chas.columns) df_preprocessed = df_wo_chas_scaled.join(df_chas_encoded) |
可視化
2次元
ここではまず、2次元可視化の結果を確認する。
クラス分類の場合は2次元で2つの主成分を確認できるが、回帰データの場合はターゲットの量を確認する必要があるため、グラフの軸を1つ消費する。このため、2次元による表現では1つの主成分による説明性を確認することになる。
- 各点の色や大きさをターゲットの値によって変化させ、2つの軸を2つの主成分に割り当てる方法も考えられるが、直感的にとらえにくくなる。
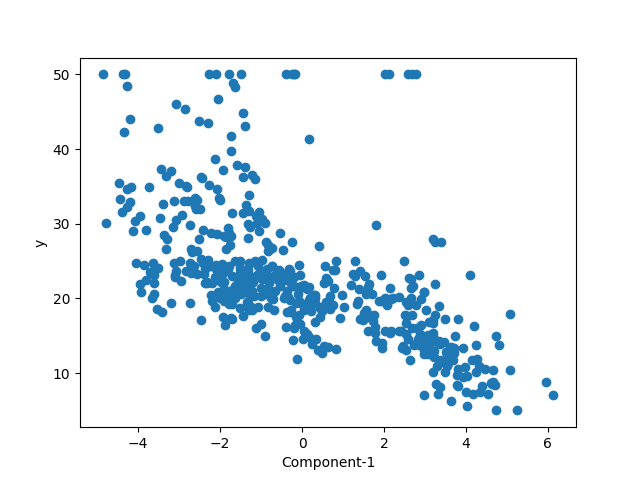
この結果を見る限り、あまり美しい結果とはなっていない。データを俯瞰した際、各特徴量であまりいい説明ができなかったが、その中でもある程度関係がみられたMDEVやLSTATとの相関と変わらないくらい。
3次元
そこで3次元の可視化にして、2つの主成分による説明性を確認する。
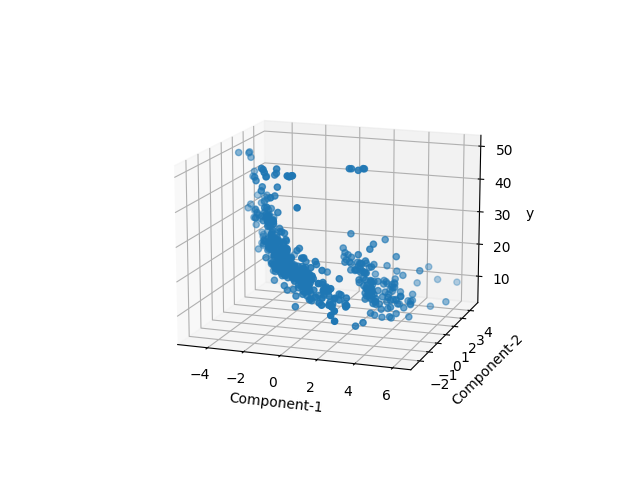
これでもあまりいい結果にならない。ただしグラフを見ると、大きく2つの塊に分かれているように見える。ターゲットである住居価格とは別に、特徴量の組み合わせに隠れている、性質の違うグループがあるのかもしれない。
主成分と寄与率
2つの主成分と寄与率について表示させてみる。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
Components: feature comp_0 comp_1 0 CRIM 0.251012 0.399530 1 ZN -0.256281 0.436197 2 INDUS 0.346630 -0.109264 3 NOX 0.342782 -0.169987 4 RM -0.189333 0.063747 5 AGE 0.313601 -0.318114 6 DIS -0.321462 0.331591 7 RAD 0.319816 0.381156 8 TAX 0.338513 0.318517 9 PTRATIO 0.205059 0.182159 10 B -0.203023 -0.333020 11 LSTAT 0.309817 -0.027564 12 CHAS_0.0 -0.001091 0.035239 13 CHAS_1.0 0.001091 -0.035239 Explained :[0.50514047 0.1109301 ] |
寄与率は第1主成分が50%程度で低いため高い相関が出ないといえるかもしれない。だが、Breast cancerデータセットのクラス分類では第1主成分の寄与率が40%台だが、明確なクラス分類ができていた。やはり回帰系の問題にはPCAは不向きなのかもしれない。
主成分の要素について、先の散布図が第1主成分と負の相関があることから、第1主成分の各特徴量は価格低下に寄与するものはプラス、価格上昇に寄与するものはマイナスとなるはずである。
たとえばZNやRMがマイナスなのは頷けるが、DISがマイナスなのは微妙。TAXやPRATIOがプラスなのも逆のような気がする。
先にも書いたが、Boston housing pricesデータセットで取りそろえられた特徴量は、住居の価格以外の何かを特徴づける傾向が強いのかもしれない。