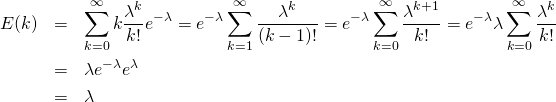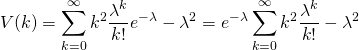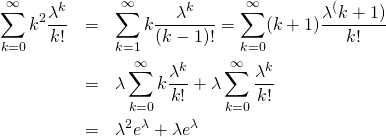投稿者: tau

R – ベクトルのソート

/ tau / コメントする

sort()関数

sort()関数で引数にベクトルを指定して、その要素をソートできる。デフォルトで昇順、decreasing属性で降順にもできる。

partial属性は、指定した位置の要素より小さい要素をその要素より前に、大きい要素を後ろに移動させる(完全なソートはしない)。

以下の例では、3番目の要素(5)より小さな要素を前へ、大きな要素を後ろへ移動させている。5の前の要素の列、後ろの列は、それぞれ必ずしもソートされない。

partial属性をベクトルで与えた場合、複数の位置の要素の前後に各要素が集められる。以下の例では、5番目の要素(5)と10番目の要素(11)が基準となり、5より小さい要素群、5と11の間の要素群、11より大きい要素群に分けられるが、それぞれは必ずしもソートされない。

ちなみにこの指定の仕方で、基準となる要素の大小関係が逆転していると、よくわからない結果になる。

rank()関数

ベクトルの要素を昇順でソートしたときの順序を要素とするベクトルを返す。

 

 

R – ベクトルの演算

/ tau / コメントする

数値演算

ベクトル同士の数値演算

同じ長さのベクトル同士の演算は、要素ごとにその演算が実行される。

ベクトルの長さが違う場合は、短い方の要素が循環して利用される。ただし長い方の要素数が短い方の要素数の整数倍になっていないと警告メッセージが出る。

ベクトルの各要素への同じ演算の適用

要素数1のベクトルを用いると、ベクトルの全要素に同じ演算を施すことができる。

比較演算

数値演算と同じく、要素ごとの比較演算も可能。要素数が違う場合も同じように循環適用される。

結果は論理型ベクトルとして返される。

数学関数

数学関数の引数にベクトルを使うと、各要素にその関数が適用される。

集合演算

ベクトルを集合とみなして、集合演算を行うことができる。

 

R – ベクトルの操作

/ tau / コメントする

要素の取得・部分ベクトルの抽出

単一要素の取得

ベクトルの要素は[]で添字を指定して参照

  • 先頭要素は(0番目ではなく)1番目
  • 要素数より大きい数を指定した場合はNAが返される
  • 0を指定した場合はnumeric(0)～0を0個並べたベクトルが返される

複数要素からなるベクトルを抽出

複数の要素をベクトル化して指定した場合は、それらの位置の要素からなるベクトルが返される。返り値のベクトルの要素の順番は引数のベクトルで指定した順番になる。

要素を除外したベクトルを取得

負の数を指定した場合は、その絶対値の位置の要素を除いたベクトルが返される。

  • 複数の要素を除外したい場合は、除外したい位置の添字をベクトル化して指定
  • 除外要素の指定は順不同
  • 返り値のベクトルの要素の順番は元のベクトルに準ずる
  • 負数を使う場合は正数は混在できない
  • 0は使えるが意味を持たない

条件を指定した要素・ベクトルの抽出

要素の代わりに条件式を指定すると、その条件に合った要素からなるベクトルが返される。

条件式を変数として書くこともできて、

  • 条件を満たす要素位置がTRUE、満たさない要素位置がFALSEという要素からなるベクトルが返される
  • そのベクトルを元のベクトルの引数として指定すると、TRUEの位置の要素からなるベクトルが返される

要素の追加・ベクトルの結合

既存のベクトルの長さ以上の要素を指定して値を代入すると、ベクトルが拡張されて値が代入される。

間が空いていればNAが代入される。

c()関数の中でベクトルと要素を列記して結合できる。複数の要素とベクトルを混在させることが可能。

append(v1, v2, after=n)関数は、v1のn番目の要素の後ろにv2を挿入。

また、以下のように現在の要素数 + 1の要素に値をセットすると要素が追加される。

要素・ベクトルの置換

replace()関数で指定位置の要素を指定した要素で置き換える。

  • 複数要素を置き換える場合は、指定位置と置き換え要素をベクトルで指定
    • 指定位置の数と置き換え要素の数が等しいこと
  • 指定位置の要素をベクトルで置き換えることはできない模様

条件を指定して、その条件を満足する要素のみ置換することも可能。

 

 

R – ベクトルの生成

/ tau / コメントする

値を直接指定して生成する

c(...)の関数の中に要素を列挙する。

同じ値が繰り返されるベクトル

要素が値の場合。

ベクトルを与えると、そのベクトルの要素が繰り返される。

ベクトルの要素を要素ごとに繰り返す。

要素ごとに繰り返しながら全体を繰り返す。timesとeachの指定順は関係しない。

一定値で増減するベクトル

1ずつ増減

[開始値]:[終了値]で指定する。

seq()関数を使っても同じ。

seq()関数の本来の表現。

1以外のステップ値で増減するベクトル

seq()関数の”by=”引数でステップ値を指定。

単に引数を3つ指定した場合は、3つ目の値が”by=”の値とみなされる。

終了値がジャストでない場合は手前まで。

ただし要素の変化方向と増減値の符号が逆の場合はエラー。

ベクトルの長さ(要素数)を指定

length.out属性で指定。

length.outの代わりにlength、lenとしてもよい。

seq_len()関数は、非負の整数で長さを与えて数列を生成。

sequence()関数

seq()関数とは違う。

引数に整数値を持つベクトルc(n1, n2, …)を指定して、各要素を終了値としたベクトル1:n1、1:n2、…を結合したベクトルを返す。

乱数列の生成

Rでは、様々な確率分布に従う乱数列を生成することができる。

基本形はr<name>(n, <parameters>)の形を取り、<name>で確率分布を、<parameters>で確率分布に対応したパラメータを指定する。

一様分布

runif(n, min=a, max=b)

(a, b)の一様分布に従う乱数をn個生成する。

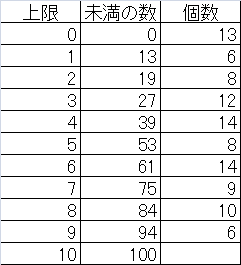
二項分布

rbinom(n, size=s, prob=p)

確率pの二項分布に従う乱数を生成する。たとえば不良品率pの部品からs個のサンプルを取り出し、不良品の数を数えるという試行をn回繰り返す、などの例に相当する。

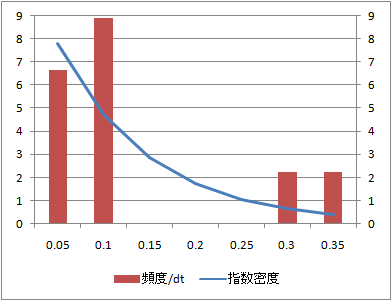
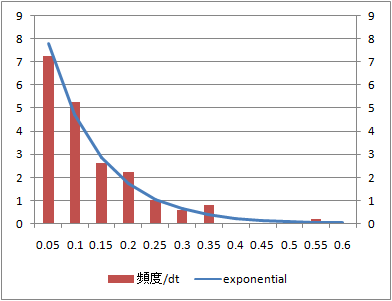
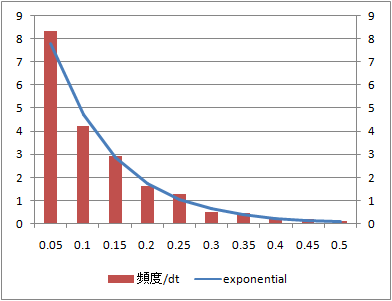
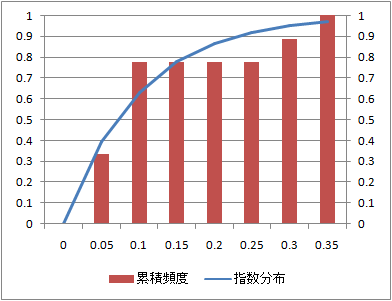
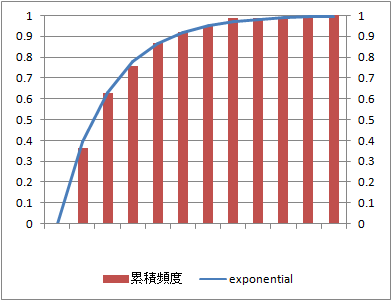
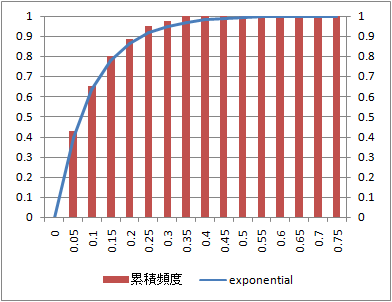
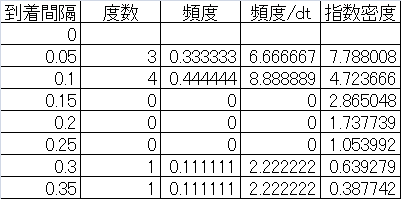
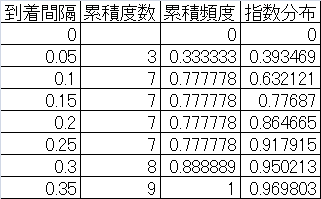
指数分布

rexp(n, rate=l)

l=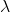\lambdaの指数分布に従う乱数を生成する。

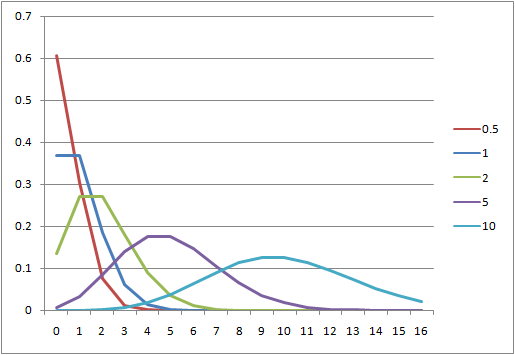
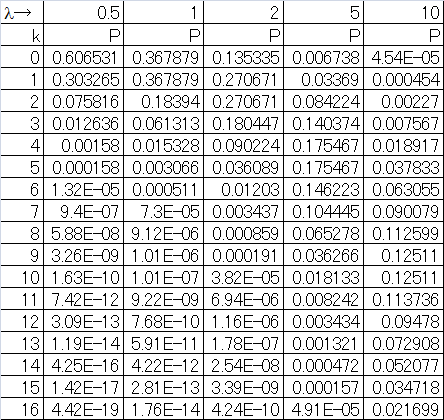
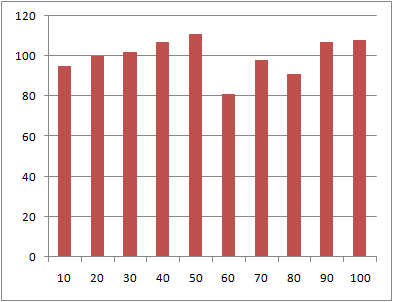
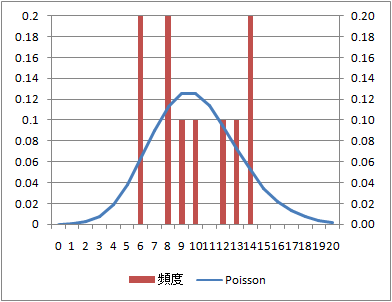
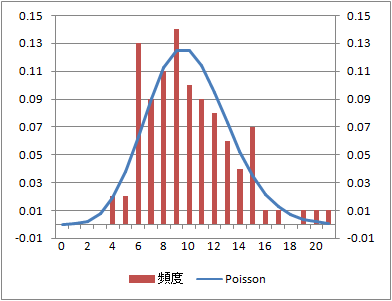
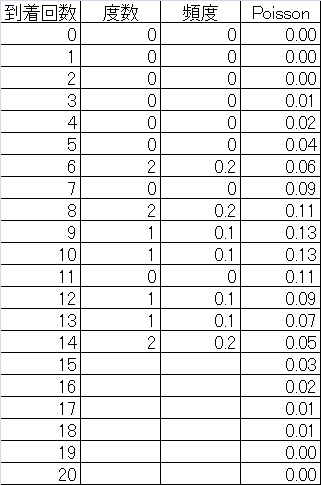
ポアソン分布

rpois(n, lambda=l)

l=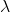\lambdaのポアソン分布に従う乱数を生成する。

正規分布

rnorm(n, mean=m, sd=s)

平均m、標準偏差sの正規分布に従う乱数を生成する。

 

R – 演算子

/ tau / コメントする

算術演算子

四則演算は他の言語と同じ。正数除算(%/%)と剰余(%%)は独特。

演算の優先順位は、

  1. ()
  2. ^
  3. %/%, %%
  4. *, /
  5. +, –

比較演算子

他の言語と同じだが、数値の同一性は一定の誤差より小さい場合に「等しい」と判定される。

論理演算子

数値に対しては他の言語と同じ

 

 

ポアソン過程について

/ tau / コメントする

概要

次のような条件で、客の到着、トランザクションやトラブルの発生といったランダム事象の発生を考える。

  • 各事象は、その前の事象の発生から影響を受けたり、その次の事象に影響を与えたりしない(無記憶性)
  • 各事象が単位時間あたりに発生する数には偏りがない(均質性)

この場合、事象の発生は時間軸上で一様分布と考えられ、定常ポアソン過程／ポアソン到着と呼ばれる。

ポアソン過程の到着数

単位時間当たりの到着数が\lambdaで与えられたとき、観測時間tの間にk回の到着が観測される確率は、以下のPoisson分布で与えられる。

(1)   \begin{equation*} P_n (X = k; t; \lambda) = \frac{(\lambda t)^k}{k!} e^{- \lambda t} \end{equation*}

この導出は”ポアソン過程の到着数～ポアソン分布“に示すが、その概略は、観測時間tを有限・等間隔の微小時間間隔\Delta tに分け、到着数がk回となる組み合わせの数を考慮しながら確率を計算し、\Delta t \to \inftyの極限をとるという操作。

このとき、到着回数の平均と分散は以下のようになるが、その導出はPoisson分布の説明を参照。

(2)   \begin{equation*} E(k) = \lambda = {\rm const} \end{equation*}

(3)   \begin{equation*} V(k) = \lambda = {\rm const} \end{equation*}

ポアソン過程の到着時間間隔

単位時間当たりの到着数が\lambdaで与えられたとき、ある到着から次の到着までの時間間隔tは指数分布に従い、その確率密度f(t)と確率分布F(t \le T)は以下のように与えられる。

(4)   \begin{equation*} f(t) = \lambda e^{- \lambda t} \end{equation*}

(5)   \begin{equation*} F(t \le T) = 1 - e^{- \lambda T} \end{equation*}

この導出は”ポアソン過程の到着間隔～指数分布“に示すが、その概略は上のPoisson分布と同じく、観測時間tを微小時間間隔に分けて、その極限をとるという操作。

このとき、到着時間間隔の平均と分散は以下のようになるが、その導出は指数分布の説明を参照。

(6)   \begin{equation*} E(k) = \frac{1}{\lambda} \end{equation*}

(7)   \begin{equation*} V(k) = \frac{1}{\lambda ^2} \end{equation*}

このほか、それぞれの確率分布の形状や考察についても、Poisson分布の説明、指数分布の説明にまとめた。

ポアソン過程のシミュレーションと確認

一様分布による到着のシミュレーション

”ポアソン過程～一様分布によるシミュレーション“で、一様分布に従う乱数を発生させて、その到着時間間隔／到着回数が指数分布／Poisson分布に従っているか確認した。

 

 

ポアソン過程～一様分布によるシミュレーション

/ tau / コメントする

概要

一様分布をとる乱数によってランダムな到着をシミュレートし、ポアソン過程の時間間隔や到着回数を理論上の確率分布と比較してみた。

手順

  1. 表計算ソフトで0 ～1の間で平均して10個の発生するように乱数を発生させる
    • 0～1で10個
    • 0～10で100個
    • 0～100で1000個
  2. その値を昇順にソート(到着事象の到着時刻順にあたる)
  3. 到着時刻の分布を確認
  4. 到着時間間隔の分布と指数分布の比較
    1. 各到着時刻間の時間間隔を計算
    2. 時間間隔データの頻度(確率密度に相当)を棒グラフで表示し、指数分布の密度関数のグラフを重ねて比較
    3. 時間間隔データの累積頻度(確率分布に相当)を棒グラフで表示し、指数分布関数のグラフを重ねて表示
  5. 到着回数の分布とPoisson分布の比較

指数分布のデータを得る手順については、 (参考)データ数10個の場合到着時間間隔の計算手順を参照。

Poisson分布のデータを得る手順については、(参考)データ数100個の場合の到着数の計算手順を参照。

以下、データ数10、100、1000の場合の到着時刻の分布、到着間隔の確率密度と確率分布について比較していく。

到着時刻の分布の比較

データ数10、100、1000に対する到着時刻の分布を以下に示す。

データ数が多くなるほどグラフは平滑になるが、1000個と比較的多くのデータでもばらつきが見られる。

データ数：10
random-arrival-verification-duration0010

データ数：100
random-arrival-verification-duration0100

データ数：1000
random-arrival-verification-duration1000

到着時間間隔と指数分布の比較

頻度(確率密度)

データ数10、100、1000に対する到着時間間隔の頻度分布とこれに相当する指数分布の確率密度関数を比較する。

到着時刻の分布に比べてデータ数100からシミュレーション値と理論値がよく整合している。

データ数：10
random-arrival-verification-exp-density0010

データ数100
random-arrival-verification-exp-density0100

データ数1000
random-arrival-verification-exp-density1000

累積頻度(確率分布)

同じデータの累積頻度とこれに相当する指数分布の確率分布関数を比較する。

確率分布に関しては、データ数10と少ないデータでも理論値と類似している。

データ数：10
random-arrival-verification-exp-prob0010

データ数：100
random-arrival-verification-exp-prob0100

データ数：1000
random-arrival-verification-exp-prob1000

到着数の分布とPoisson分布の比較

到着数の分布をみるためには、データ数10個の場合はデータセットにならないため、データ数100、1000で比較してみる。データ数100を10組に、データ数100は100組のデータセットを得ることができる。

到着数の分布と理論上のPoisson分布との整合性は、データセット数100でもそれほどよくない。

データ数：100(データセット数：10)
random-arrival-verification-poisson-prob0100

データ数：1000(データセット数100)
random-arrival-verification-poisson-prob1000

(参考)データ数10個の場合到着時間間隔の計算手順

以下の表は、0～1の範囲で10個の乱数を発生させ、それらを昇順にソートして発生間隔を計算したもの。

statistics-random-arrival-verification-1

まず、これらの発生時刻を、一定の階級幅で度数分布に分ける。データ数が10個の場合はばらつきが大きいが、データ数が多くなると、これが一様分布に近づくと期待される。

statistics-random-arrival-verification-2

次に、到着時間間隔の度数分布とその頻度を計算する。これを指数分布の密度関数と比較するため、時間間隔dtで除している。一番右の欄は、到着率10の指数分布の密度関数の値。

statistics-random-arrival-verification-3

最後に、指数分布の確率関数と比較をするため、到着間隔の累積度数と頻度を計算する。一番右の欄は、到着率10の確率分布関数の値。

statistics-random-arrival-verification-4

(参考)データ数100個の場合の到着数の計算手順

元データは、到着時刻を昇順にソートしたもの。

 random-arrival-verification-poisson1

これらのデータの、0以上1未満、1以上2未満、・・・・、9以上10未満の10組ごとのデータ数を数える。

random-arrival-verification-poisson2

これらについて、到着回数ごとの頻度分布に整理する。下表一番右の欄は、到着率10に対するPoisson確率値。

random-arrival-verification-poisson3

 

ポアソン過程の到着数～ポアソン分布

/ tau / コメントする

単位時間当たりの到着率\lambdaのポアソン過程において、t時間の間にk回の到着が発生する確率を考える。

tをn等分し、\Delta t = t / nとする。この間にk回の到着が発生し、(n - k)回は到着が発生しないとすると、その確率は次の二項分布で表される。

(1)   \begin{equation*} P(k;t;n) = {}_n C_k (\lambda \Delta t)^k (1 - \lambda \Delta t)^{n-k} \end{equation*}

この式を、以下のように展開しておく。

(2)   \begin{eqnarray*} P(k;t;n) &=& \frac{n!}{k! (n-k)!} (\lambda \Delta t)^k (1 - \lambda \Delta t)^{n - k} \\ &=& \frac{n(n - 1) \cdots (n - k + 1)}{k!} \left( \frac{\lambda t}{n} \right)^k \left(1 - \frac{\lambda t}{n} \right)^{n - k} \end{eqnarray*}

ここでn \to \infty (\Delta t \rightarrow 0)の極限を考える。まず前2項については、

(3)   \begin{eqnarray*} &&\lim_{n \to \infty} \frac{n(n - 1) \cdots (n - k + 1)}{k!} \left( \frac{\lambda t}{n} \right)^k \\ &=& \lim_{n \to \infty} \frac{1 \cdot \left(1 - \cfrac{1}{n} \right) \cdots \left(1 - \cfrac{k - 1}{n} \right)}{k!} (\lambda t)^k \\ &=& \frac{(\lambda t)^k}{k!} \end{eqnarray*}

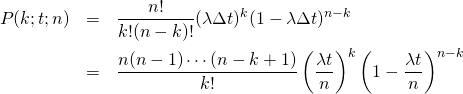
また3項目については-n / \lambda t = r \to \inftyとおいて、

(4)   \begin{equation*} \lim_{r \to \infty} \left( 1 + \frac{1}{r} \right)^{- r \lambda t - k} = \lim_{r \to \infty}\left[ \left(1 + \frac{1}{r} \right)^{- r \lambda t} \left( 1 + \frac{1}{r} \right)^{-k} \right] = e^{- \lambda t} \end{equation*}

通常、Poisson分布の表現は上式において\lambda t \to \lambdaとして表現されるが、この場合の\lambdaは観測時間内の平均到着数として考える。ここでは、単位時間あたりの到着率\lambdaと観測時間tを明確にするため\lambda tと表現した。

以上から、到着率\lambdaのポアソン過程において、観測時間tの間にk回の到着が発生する確率は以下のPoisson分布で与えられる。

(5)   \begin{equation*} P(k; t; \lambda) = \frac{(\lambda t)^k}{k!} e^{- \lambda t} \end{equation*}

 

 

ポアソン過程の到着間隔～指数分布

/ tau / コメントする

離散的な方法による確認

単位時間あたりの到着率\lambdaのポアソン過程において、時刻0に到着が発生した後、次の到着があるまでの時間間隔がt以下である確率を考える。

tをn等分し、\Delta t = t / nとすると、到着間隔がt以下なので、連続して到着しなかった後に到着が発生する事象を重ね合わせて、以下のように表せる。

(1)   \begin{eqnarray*} P(\tau \le t) &=& \lambda \Delta t + (1 - \lambda \Delta t)\lambda \Delta t + \cdots + (1 - \lambda \Delta t)^{n-1} \lambda \Delta t \\ &=& \lambda \Delta t \frac{1 - (1 - \lambda \Delta t)^n}{1 - (1 - \lambda \Delta t)} \\ &=& 1 - \left( 1 - \frac{\lambda t}{n} \right) \end{eqnarray*}

ここで-n/\lambda t = rとおいてr \to \inftyの極限をとると、

(2)   \begin{equation*} \lim_{r \to \infty} 1 - \left( 1 + \frac{1}{r} \right)^{-r \lambda t} = 1 - e^{- \lambda t} \end{equation*}

となって指数分布の確率分布関数を得る。

確率密度関数を直接求める方法

到着時間間隔の確率密度関数をf(x)とし、0 \sim tの間は到着が発生せず、t \sim t + \Delta tで到着が発生する場合を考える。

(3)   \begin{equation*} f(t) \Delta t = \left( 1 - \int_0^t f(t) dt \right) \lambda \Delta t \end{equation*}

これより、

(4)   \begin{equation*} f(t) = \lambda - \lambda \int_0^t f(t) dt \end{equation*}

両辺をtで微分して、

(5)   \begin{equation*} f'(t) = - \lambda f(t) \end{equation*}

この微分方程式の解は、

(6)   \begin{equation*} f(t) = C e^{- \lambda t} \end{equation*}

確率密度関数なので、全定義域の積分値が1となることから、

(7)   \begin{equation*} \int_0^\infty C e^{- \lambda t} dt = \left[ - \frac{C}{\lambda} e^{- \lambda t} \right]_0^\infty = 1 \end{equation*}

これよりC = \lambdaを得るので、確率密度関数は以下のように得られる。

(8)   \begin{equation*} f(t) = \lambda e^{- \lambda t} \end{equation*}

Poisson分布から導く方法

ポアソン過程に関して、以下のPoisson分布を考える。

(9)   \begin{equation*} P(X = k) = \frac{(\lambda t)^k}{k!} e^{- \lambda t} \end{equation*}

ここで、時刻T = 0 \sim tの間に全く到着がない確率はその時間の間k = 0であるから、

(10)   \begin{equation*} F(T > t) = e^{- \lambda t} \end{equation*}

ここで、到着時間間隔がt以下である確率は、T = 0 \sim tの間に1回以上到着がある事象の和であり、「1回も到着がない」事象の余事象でもある。これより、以下の指数分布の分布関数を得る。

(11)   \begin{equation*} F(T \le t) = 1 - e^{- \lambda t} \end{equation*}

 

ポアソン分布

/ tau / コメントする

Poisson分布の標準形

ポアソン過程の到着数に現れる、離散確率分布。

(1)   \begin{equation*} P(k; \lambda) = \frac{\lambda ^ k}{k!} e^{- \lambda} \end{equation*}

全事象の確率が1となることの確認

(2)   \begin{equation*} \sum_{k=0}^{\infty} \frac{\lambda ^ k}{k!} e^{- \lambda} = e^{\lambda} e^{-\lambda} = 1 \end{equation*}

平均

(3)   \begin{eqnarray*} E(k) &=& \sum_{k=0}^{\infty} k \frac{\lambda ^ k}{k!} e^{- \lambda} = e^{-\lambda} \sum_{k=1}^{\infty} \frac{\lambda ^ k}{(k - 1)!} = e^{-\lambda} \sum_{k=0}^{\infty} \frac{\lambda ^ {k + 1}}{k!} = e^{-\lambda} \lambda \sum_{k=0}^{\infty} \frac{\lambda ^ {k}}{k!} \\ &=& \lambda e^{-\lambda} e^{\lambda} \\ &=& \lambda \end{eqnarray*}

この過程で以下のようになっていることに留意。

(4)   \begin{eqnarray*} \sum_{k=0}^{\infty} k \frac{\lambda ^ k}{k!} &=& 0\cdot \frac{\lambda ^0}{0!} + 1 \cdot \frac{\lambda ^1}{1!} + 2 \cdot \frac{\lambda ^2}{1 \cdot 2} + 3 \cdot \frac{\lambda ^3}{1 \cdot 2 \cdot 3} + \cdots + k\frac{\lambda ^k}{1 \cdots k} + \cdots \\ &=& \frac{\lambda ^1}{1} + \frac{\lambda ^2}{1} + \frac{\lambda ^3}{1 \cdot 2} + \cdots + \frac{\lambda ^k}{1 \cdots (k-1)} + \cdots \left( = \sum_{k=1}^{\infty} \frac{\lambda ^ k}{(k - 1)!} \right) \\ &=& \frac{\lambda ^1}{0!} + \frac{\lambda ^2}{1!} + \frac{\lambda ^3}{2!} + \cdots + \frac{\lambda ^{k}}{k-1} + \cdots \left( = \sum_{k=0}^{\infty} \frac{\lambda ^ {k + 1}}{k!} \right) \\ &=& \lambda \sum_{k=0}^{\infty} \frac{\lambda ^k}{k!} \end{eqnarray*}

分散

(5)   \begin{equation*} V(k) &=& \sum_{k=0}^{\infty} k^2 \frac{\lambda ^k}{k!} e^{- \lambda} - \lambda^2 = e^{- \lambda} \sum_{k=0}^{\infty} k^2 \frac{\lambda ^k}{k!} - {\lambda}^2 \end{equation*}

第一項の和の部分については、

(6)   \begin{eqnarray*} \sum_{k=0}^{\infty} k^2 \frac{\lambda ^k}{k!} &=& \sum_{k=1}^{\infty} k \frac{\lambda ^k}{(k - 1)!} = \sum_{k=0}^{\infty} (k + 1) \frac{\lambda ^(k + 1)}{k!} \\ &=& \lambda \sum_{k=0}^{\infty} k \frac{\lambda ^k}{k!} + \lambda \sum_{k=0}^{\infty} \frac{\lambda ^k}{k!} \\ &=& \lambda ^2 e^\lambda + \lambda e^\lambda \end{eqnarray*}

したがって分散は以下のように得られる。

(7)   \begin{equation*} V(k) = \lambda \end{equation*}

確率分布の形状と考察

Poisson分布の形状の特徴は以下の通り。

  • \lambda < 1のときは単調減少
  • \lambda = 1のときk = 0, 1に対する確率が等しく、約0.368
  • \lambda > 1でピークが現れる。

statistics-poisson-distribution

statistics-poisson-table

\lambda < 1は、その観測期間内に平均して1回も来ないようなケース。たとえば\lambda = 0.5だと、平均して20分に1度来訪者が来ているとき次の10分に何人来そうか？といったイメージで、全く来ない確率が約60%、1人来る確率が約30%、2人以上来る確率が1割程度となる。ランダム事象と仮定したときの、災害に当てはめても興味深い。

\lambda = 1は、単位時間あたりの到着率に観測時間を乗じた値が1ということであり、平均的にその観測時間内に1回到着しそうな状況にあたる。このような状況でも全く到着がない確率と1回到着する確率が等しく約37%、2回以上到着する確率が25%強となる。

\lambda > 1の場合、\lambdaの値に近いところで確率が最大となり、\lambdaの値が大きくなるにしたがって高さは低く、裾野が広くなり対称形に近くなる。