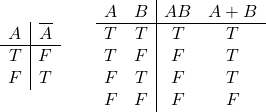
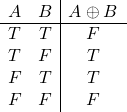
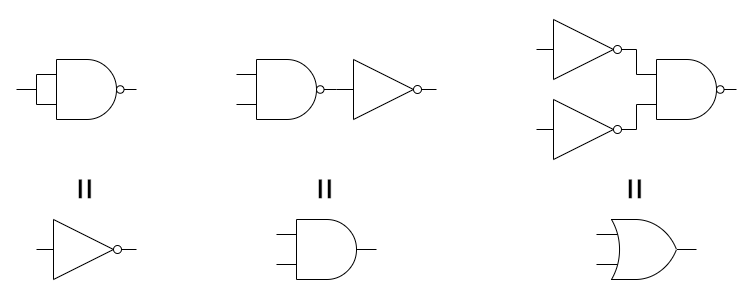
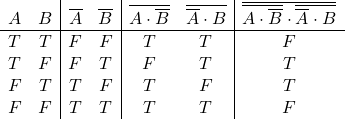
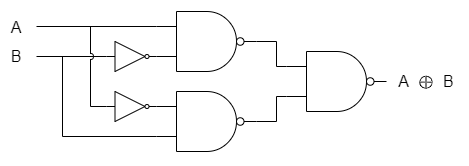
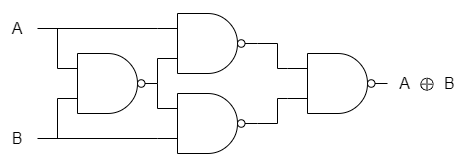
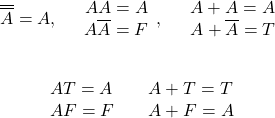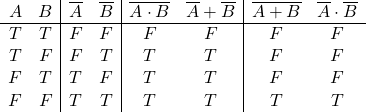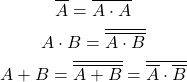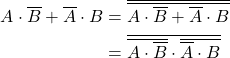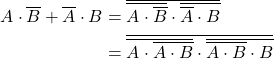Java – 配列 – 多次元配列

2021-06-03 / tau / コメントする

初期化

多次元配列の型はtype[][]...で表し、1次元と同じくイニシャライザーやnewで初期化できる。

newとイニシャライザーを使うと、要素配列を個別に定義することが可能。

import java.util.Arrays;

public class ArrayMultiDimensional {
  public static void main(String[] args) {
    // イニシャライザーによる初期化
    int[][] intArray = {{0, 1}, {2, 3, 4}};
    System.out.println(Arrays.deepToString(intArray));
    // [[0, 1], [2, 3, 4]]

    // newとイニシャライザーによる初期化
    intArray = new int[][] {{5, 6, 7}, {8, 9}};
    System.out.println(Arrays.deepToString(intArray));
    // [[5, 6, 7], [8, 9]]

    // newとイニシャライザーによる要素配列ごとの初期化
    intArray = new int[3][];
    intArray[0] = new int[] {1, 2, 3};
    intArray[1] = new int[] {4, 5, 6};
    intArray[2] = new int[] {7, 8, 9};
    System.out.println(Arrays.deepToString(intArray));
    // [[1, 2, 3], [4, 5, 6], [7, 8, 9]]
  }

}

import java.util.Arrays;

public class ArrayMultiDimensional {

public static void main(String[] args) {

// イニシャライザーによる初期化

int[][] intArray = {{0, 1}, {2, 3, 4}};

System.out.println(Arrays.deepToString(intArray));

// [[0, 1], [2, 3, 4]]

// newとイニシャライザーによる初期化

intArray = new int[][] {{5, 6, 7}, {8, 9}};

System.out.println(Arrays.deepToString(intArray));

// [[5, 6, 7], [8, 9]]

// newとイニシャライザーによる要素配列ごとの初期化

intArray = new int[3][];

intArray[0] = new int[] {1, 2, 3};

intArray[1] = new int[] {4, 5, 6};

intArray[2] = new int[] {7, 8, 9};

System.out.println(Arrays.deepToString(intArray));

// [[1, 2, 3], [4, 5, 6], [7, 8, 9]]

}

内容表示

多次元配列を表示するには、ループで回すかArrays.deepToString()を使う(Java – 配列 – 内容表示)。

import java.util.Arrays;

public class ArrayMultiDim {
  public void display() {
    int[][] intArray = {{0, 1}, {2, 3, 4}};

    for (int[] subarray: intArray) {
      for (int e: subarray) {
        System.out.print(e + " ");
      }
      System.out.println();
    }
    // 0 1 
    // 2 3 4 

    System.out.println(Arrays.deepToString(intArray));
    // [[0, 1], [2, 3, 4]]
  }

  public static void main(String[] args) {
    ArrayMultiDim app = new ArrayMultiDim();
    app.display();
  }
}

import java.util.Arrays;

public class ArrayMultiDim {

public void display() {

int[][] intArray = {{0, 1}, {2, 3, 4}};

for (int[] subarray: intArray) {

for (int e: subarray) {

System.out.print(e + " ");

}

System.out.println();

}

// 0 1

// 2 3 4

System.out.println(Arrays.deepToString(intArray));

// [[0, 1], [2, 3, 4]]

}

public static void main(String[] args) {

ArrayMultiDim app = new ArrayMultiDim();

app.display();

}

Java – 配列 – 内容表示

2021-06-03 / tau / コメントする

そのままだとオブジェクトの表示

Javaの配列をそのまま表示しようとすると、参照値が表示される。

int[] intArray = {0, 2, 4, 6};

System.out.println(intArray);
// [I@7637f22

int[] intArray = {0, 2, 4, 6};

System.out.println(intArray);

// [I@7637f22

Arrays.toString()

配列の内容を文字列として表現するには、java.util.ArraysのtoString()メソッドを使う。

System.out.println(java.util.Arrays.toString(intArray));
// [0, 2, 4, 6]

1 2	System.out.println(java.util.Arrays.toString(intArray)); // [0, 2, 4, 6]

多次元配列の場合

多次元配列の親配列をtoString()で表示しても下位次元までは適切に表示してくれない。

String[][] twoDimArray = {{"zero", "one", "two"}, {"three", "four", "five"}};

System.out.println(java.util.Arrays.toString(twoDimArray));
// [[Ljava.lang.String;@3830f1c0, [Ljava.lang.String;@39ed3c8d]

String[][] twoDimArray = {{"zero", "one", "two"}, {"three", "four", "five"}};

System.out.println(java.util.Arrays.toString(twoDimArray));

// [[Ljava.lang.String;@3830f1c0, [Ljava.lang.String;@39ed3c8d]

ループによる表示

ループを回して表示させることは考えられる。

for (String[] subarray: twoDimArray) {
  System.out.println(java.util.Arrays.toString(subarray));
}
// [zero, one, two]
// [three, four, five]

for (String[] subarray: twoDimArray) {

System.out.println(java.util.Arrays.toString(subarray));

}

// [zero, one, two]

// [three, four, five]

Arrays.deepToString()

Arrays.deepToString()メソッドを使うと、多次元配列の内容を手軽に表示できる。

String[][] twoDimArray = {{"zero", "one", "two"}, {"three", "four", "five"}};

System.out.println(java.util.Arrays.deepToString(twoDimArray));
// [[zero, one, two], [three, four, five]]

String[][] twoDimArray = {{"zero", "one", "two"}, {"three", "four", "five"}};

System.out.println(java.util.Arrays.deepToString(twoDimArray));

// [[zero, one, two], [three, four, five]]

Java – 配列 – 長さ(サイズ)

2021-06-03 / tau / コメントする

配列の長さ(サイズ)はlengthプロパティーで得られる。Stringの場合のlength()メソッドと異なるので注意。

String[] strArray = {"one", "two", "three", "four"};
System.out.println(strArray.length);
// 4

String[] strArray = {"one", "two", "three", "four"};

System.out.println(strArray.length);

// 4

多次元配列の場合、親の配列の長さは子配列の数になる。

int[][] intArray = {{1, 2, 3}, {4, 5, 6, 7}};

System.out.println(intArray.length);    // 2
System.out.println(intArray[0].length); // 3
System.out.println(intArray[1].length); // 4

int[][] intArray = {{1, 2, 3}, {4, 5, 6, 7}};

System.out.println(intArray.length); // 2

System.out.println(intArray[0].length); // 3

System.out.println(intArray[1].length); // 4

Java – 配列 – 初期化

2021-06-03 / tau / コメントする

イニシャライザーによる初期化

全要素が同じ型の配列をイニシャライザーで初期化する書き方。typeはプリミティブ型でも参照型でもよい。

type[] arrayName = {emelent1, emenent2, ...};

import java.util.Arrays;

public class ArrayInit {
  public void initializer() {
    int[] intArray = {0, 2, 4, 6};
    System.out.println(Arrays.toString(intArray));
    // [0, 2, 4, 6]

    String[] stringArray = {"zero", "two", "four", "six"};
    System.out.println(Arrays.toString(stringArray));
    // [zero, two, four, six]
  }

  public static void main(String[] args) {
    ArrayInit app = new ArrayInit();
    app.initializer();
  }
}

import java.util.Arrays;

public class ArrayInit {

public void initializer() {

int[] intArray = {0, 2, 4, 6};

System.out.println(Arrays.toString(intArray));

// [0, 2, 4, 6]

String[] stringArray = {"zero", "two", "four", "six"};

System.out.println(Arrays.toString(stringArray));

// [zero, two, four, six]

}

public static void main(String[] args) {

ArrayInit app = new ArrayInit();

app.initializer();

}

newによる初期化

newによる配列インスタンスの生成の書き方。typeはプリミティブ型でも参照型でもよい。

type[] arrayName = new type[length];

以下の例では、配列を生成した後に一つずつ要素を定義している。

import java.util.Arrays;

public class ArrayInit {
  public void initByNew() {
    int[] intArray = new int[4];

    intArray[0] = 0;
    intArray[1] = 2;
    intArray[2] = 4;
    intArray[3] = 6;

    System.out.println(Arrays.toString(intArray));
    // [0, 2, 4, 6]
  }

  public static void main(String[] args) {
    ArrayInit app = new ArrayInit();
    app.initByNew();
  }
}

import java.util.Arrays;

public class ArrayInit {

public void initByNew() {

int[] intArray = new int[4];

intArray[0] = 0;

intArray[1] = 2;

intArray[2] = 4;

intArray[3] = 6;

System.out.println(Arrays.toString(intArray));

// [0, 2, 4, 6]

}

public static void main(String[] args) {

ArrayInit app = new ArrayInit();

app.initByNew();

}

newによる初期化直後の値はプリミティブ型ならそれぞれのデフォルト値、参照型ならnullになる。

import java.util.Arrays;

public class ArrayInit {
  public void defaultValues() {
    boolean[] boolArray = new boolean[4];
    System.out.println(Arrays.toString(boolArray));
    // [false, false, false, false]

    int[] intArray = new int[4];
    System.out.println(Arrays.toString(intArray));
    // [0, 2, 4, 6]

    double[] dblArray = new double[4];
    System.out.println(Arrays.toString(dblArray));
    // [0.0, 0.0, 0.0, 0.0]

    char[] charArray = new char[4];
    System.out.println(Arrays.toString(charArray));
    // [, , , ]

    String[] strArray = new String[4];
    System.out.println(Arrays.toString(strArray));
    // [null, null, null, null]

    Object[] objArray = new Object[4];
    System.out.println(Arrays.toString(objArray));
    // [null, null, null, null]
  }

  public static void main(String[] args) {
    ArrayInit app = new ArrayInit();
    app.defaultValues();
  }
}

import java.util.Arrays;

public class ArrayInit {

public void defaultValues() {

boolean[] boolArray = new boolean[4];

System.out.println(Arrays.toString(boolArray));

// [false, false, false, false]

int[] intArray = new int[4];

System.out.println(Arrays.toString(intArray));

// [0, 2, 4, 6]

double[] dblArray = new double[4];

System.out.println(Arrays.toString(dblArray));

// [0.0, 0.0, 0.0, 0.0]

char[] charArray = new char[4];

System.out.println(Arrays.toString(charArray));

// [, , , ]

String[] strArray = new String[4];

System.out.println(Arrays.toString(strArray));

// [null, null, null, null]

Object[] objArray = new Object[4];

System.out.println(Arrays.toString(objArray));

// [null, null, null, null]

}

public static void main(String[] args) {

ArrayInit app = new ArrayInit();

app.defaultValues();

}

newによる初期化とイニシャライザー

配列宣言時ではなく、宣言済みの配列変数をイニシャライザーで初期化する書き方。

単にイニシャライザーで代入しようとするとエラーになるので、newによる配列の生成とイニシャライザーによる定義を同時に行う。

1つ目のint[]に関してはイニシャライザーによる初期化と同じだが、2つ目のString[]のように一度宣言された変数に対して新たな配列で初期化する場合に有効。

import java.util.Arrays;

public class ArrayInit {
  public void newWithInitializer() {
    int[] intArray = new int[] {0, 1, 2};
    System.out.println(Arrays.toString(intArray));
    // [0, 1, 2]

    String[] strArray = null;
    strArray = new String[] {"A", "B", "C"};
    System.out.println(Arrays.toString(strArray));
    // [A, B, C]
  }

  public static void main(String[] args) {
    ArrayInit app = new ArrayInit();
    app.newWithInitializer();
  }
}

import java.util.Arrays;

public class ArrayInit {

public void newWithInitializer() {

int[] intArray = new int[] {0, 1, 2};

System.out.println(Arrays.toString(intArray));

// [0, 1, 2]

String[] strArray = null;

strArray = new String[] {"A", "B", "C"};

System.out.println(Arrays.toString(strArray));

// [A, B, C]

}

public static void main(String[] args) {

ArrayInit app = new ArrayInit();

app.newWithInitializer();

}

Java – プリミティブ型のリテラル

2021-06-03 / tau / コメントする

論理型

論理型のリテラルはtrue、falseの2つ。

System.out.println(true);           // true
System.out.println(false);          // false
System.out.println(!true);          // false
System.out.println(!false);         // true
System.out.println(true && false);  // false
System.out.println(true || false);  // true

System.out.println(true); // true

System.out.println(false); // false

System.out.println(!true); // false

System.out.println(!false); // true

System.out.println(true && false); // false

System.out.println(true || false); // true

整数型

int/short/byte

各基数による表現

intの範囲以内の整数は10進、2進、8進、16進で表現可能。

8進表現は頭に’0‘を付ける。以下の表現は8進で表現できない値を指定していることになって、エラーになる。10進や16進表現で要注意。

08、09→範囲外
0a、0bなど→構文エラー

基数	例	範囲
10進	63	-2147483648～2147483647
2進	0b111111	`0b0`～ `0b11111111111111111111111111111111`
8進	077	`00`～`037777777777`？
16進	0x3f	`0x0`～`0ffffffff`

型

整数系のリテラルは、各型で表現できる範囲とビットパターンとの関係で注意が必要。

たとえばbyte型の表現範囲は−128～127で、当然以下のような代入は可能だが、これを超える値は代入できない。

byte b;
b = -128;
b = 127;
b = -129; // コンパイルエラー
b = 128;  // コンパイルエラー

byte b;

b = -128;

b = 127;

b = -129; // コンパイルエラー

b = 128; // コンパイルエラー

一方、2進や16進で表現した場合のリテラルは、型によって解釈の仕方が変わるため、代入結果の値に注意が必要。

たとえば2進数0b1111|1111(16進数0xff)は、byte型なら2の補数表現で−1、short型やint型など9ビット以上を扱えるなら、9ビット目以上が0で埋められて255となる。

short s = 0b11111111; System.out.println(s);      // 255
byte b = (byte)0b11111111; System.out.println(b); // -1

1 2	short s = 0b11111111; System.out.println(s); // 255 byte b = (byte)0b11111111; System.out.println(b); // -1

最上位ビットが8ビット目や16ビット目でそれが1の場合、正数で解釈できる型になり、敢えて補数でマイナス表現としたいときには(byte)などでキャストする必要がある。

符号

各表現に+/-をつけることができて、−をつけると負数になる。

System.out.println(-63);       // -63
System.out.println(-0b111111); // -63
System.out.println(-077);      // -63
System.out.println(-0x3f);     // -63

System.out.println(-63); // -63

System.out.println(-0b111111); // -63

System.out.println(-077); // -63

System.out.println(-0x3f); // -63

各基数による表現を正規表現で表すと以下のような感じか。

10進	`^[+-]?[1-9][0-9]*$`(ただし範囲内)
2進	`^[+-]?0b0*1[01]{0,31}$`
8進	`^[+-]?0+[1-4]?[0-7]{0,10}$`
16進	`^[+-]?0x0*[0-9A-Fa-f]{0,8}$`

long

long型の整数は末尾にl/Lをつける。

int型の範囲内の数でも末尾にLをつけるとlong型になる
int型の範囲を超える数は末尾にLが必須。

System.out.println(1L);           // int以下の範囲でもL/lをつけるとlong型
System.out.println(2147483647);   // intの最大値
System.out.println(2147483648L);  // intの範囲を超える場合はL/lが必要
System.out.println(0xffffffff);   // 2進/16進表記の限界、intでは-1
System.out.println(0xffffffffL);  // long型を明示すると正数の4294967295
System.out.println(0x100000000L); // intの範囲を超える場合はL/lが必要(4294967296)
System.out.println(9223372036854775807L);  // longの最大値(L/lは必須)
// System.out.println(9223372036854775808L);  // longの範囲外は扱えない

System.out.println(1L); // int以下の範囲でもL/lをつけるとlong型

System.out.println(2147483647); // intの最大値

System.out.println(2147483648L); // intの範囲を超える場合はL/lが必要

System.out.println(0xffffffff); // 2進/16進表記の限界、intでは-1

System.out.println(0xffffffffL); // long型を明示すると正数の4294967295

System.out.println(0x100000000L); // intの範囲を超える場合はL/lが必要(4294967296)

System.out.println(9223372036854775807L); // longの最大値(L/lは必須)

// System.out.println(9223372036854775808L); // longの範囲外は扱えない

8進表記の不思議

8進数の場合が不規則。以下の様に2進表記の32ビットを3ビットごとに区切れば8進表示となる。

0b01|11-1|111|-111|1-11|11-1|111|-111|1-11|11-1|111
= 017777777777

0b11|11-1|111|-111|1-11|11-1|111|-111|1-11|11-1|111
= 037777777777

これから、8進表示の整数リテラルの上限は037777777777(10進で−1)となりそうだが、実際には047777777777まで通る。

System.out.println(07777777777);  // 1073741823
System.out.println(017777777777); // 2147483647
System.out.println(020000000000); // -2147483648
System.out.println(020000000001); // -2147483647
System.out.println(037777777777); // -1
System.out.println(040000000000); // 0
System.out.println(040000000001); // 1
System.out.println(047777777777); // 1073741823
// System.out.println(050000000000); // 範囲外エラー

System.out.println(07777777777); // 1073741823

System.out.println(017777777777); // 2147483647

System.out.println(020000000000); // -2147483648

System.out.println(020000000001); // -2147483647

System.out.println(037777777777); // -1

System.out.println(040000000000); // 0

System.out.println(040000000001); // 1

System.out.println(047777777777); // 1073741823

// System.out.println(050000000000); // 範囲外エラー

実数型

double/float

Javaの実数型は浮動小数点形式のfloatとdoubleの2つ。

小数点表示をした場合はdoubleとして解釈され、これにfをつけるとfloatで解釈される。

System.out.println(1 / 3);    // 0
System.out.println(1.0 / 3);  // 0.3333333333333333
System.out.println(1.0f / 3); // 0.33333334

System.out.println(1 / 3); // 0

System.out.println(1.0 / 3); // 0.3333333333333333

System.out.println(1.0f / 3); // 0.33333334

小数点と整数部か小数部のいずれかがあれば実数型に解釈される。

System.out.println(1. / 3);   // 0.3333333333333333
System.out.println(.1 / 3);   // 0.03333333333333333
System.out.println(1.f / 3);  // 0.33333334
System.out.println(.1f / 3);  // 0.033333335

System.out.println(1. / 3); // 0.3333333333333333

System.out.println(.1 / 3); // 0.03333333333333333

System.out.println(1.f / 3); // 0.33333334

System.out.println(.1f / 3); // 0.033333335

整数表現にfをつけるとfloat、dをつけるとdoubleに解釈される。

System.out.println(1f / 3);   // 0.33333334
System.out.println(1d / 3);   // 0.3333333333333333

1 2	System.out.println(1f / 3); // 0.33333334 System.out.println(1d / 3); // 0.3333333333333333

文字型

char

文字指定

文字リテラルは、1文字をシングルクォート(')で囲む。全角文字もそのまま。2文字以上はエラー。

System.out.println('K');    // K
System.out.println('あ');   // あ
System.out.println('KLM');  // エラー：文字定数が無効

System.out.println('K'); // K

System.out.println('あ'); // あ

System.out.println('KLM'); // エラー：文字定数が無効

ダブルクォートで囲まれた場合は文字列(String)であり、char型ではない。charはプリミティブ型、Stringは参照型なのでキャストもできない。

System.out.println("M");  // M→Stringとして表示されている
char c = "M";             // 型の不一致: String から char には変換できません

1 2	System.out.println("M"); // M→Stringとして表示されている char c = "M"; // 型の不一致: String から char には変換できません

エスケープ

シングルクォートや改行コード、タブコードなどの特殊文字はエスケープして定義する。

System.out.print('\'');
System.out.print('1');
System.out.print('\t');
System.out.print('2');
System.out.println('\'');
// '1  2'

System.out.print('\'');

System.out.print('1');

System.out.print('\t');

System.out.print('2');

System.out.println('\'');

// '1 2'

ユニコード指定

文字リテラルは、ユニコードのコードポイントでも指定可能。その場合、シングルクォートの中で\uでコードポイントを指定する。

ただしシングルクォートのコードポイント\u0027を指定すると文字定数が無効のエラーになる。ユニコードがコンパイルされたときに'''というリテラルになるためか。

System.out.println('\u004b'); // K
System.out.println('\u3042'); // あ
//  System.out.println('\u0027'); // エラー：文字定数が無効

System.out.println('\u004b'); // K

System.out.println('\u3042'); // あ

// System.out.println('\u0027'); // エラー：文字定数が無効

Java – プリミティブ型

2021-06-03 / tau / コメントする

論理型

boolean

true/falseの二値。2値を表すのには1ビットで十分だが、実装上の内部表現については明確に定められていないらしい。

リテラル表現はtrue、false
比較式の評価結果は論理値を持つ
他の型へはキャストできない

boolean boolTrue = true;
boolean boolFalse = false;

System.out.println(boolTrue);   // true
System.out.println(boolFalse);  // false

System.out.println(1 == 1);     // true
System.out.println(1 == 0);     // false。

boolean boolTrue = true;

boolean boolFalse = false;

System.out.println(boolTrue); // true

System.out.println(boolFalse); // false

System.out.println(1 == 1); // true

System.out.println(1 == 0); // false。

数値型(整数型)

byte

8ビットの符号付き2進数で表現可能な整数で、範囲は−128～127。内部表現のサイズは1バイト。

byte型で表現可能な最大値127を超えると8ビット目が1となって負数になる
byte型で表現された−1(0b11111111)の演算結果がこれを超える場合、9ビット目以上が無視される
符号なしで8ビット目が1となるリテラル(0b1000000、0x80)以上の数はint型で解釈され、byte型へのキャストが必要
- 8ビット目が1のリテラルをbyte型にキャストした場合、負数とみなされる

byte b = 0;               // 0はそのままbyteとして解釈される
System.out.println(b);    // 0

b = 0b01111111;           // byte型の正数上限
System.out.println(b);    // 127
System.out.println(++b);  // byte型では負数となり-128

b = (byte)0b11111111;     // int型の正数として解釈→キャストが必要
System.out.println(b);    // -1
System.out.println(++b);  // byte型の範囲で循環して0

byte b = 0; // 0はそのままbyteとして解釈される

System.out.println(b); // 0

b = 0b01111111; // byte型の正数上限

System.out.println(b); // 127

System.out.println(++b); // byte型では負数となり-128

b = (byte)0b11111111; // int型の正数として解釈→キャストが必要

System.out.println(b); // -1

System.out.println(++b); // byte型の範囲で循環して0

short

16ビットの符号付き2進数で表現可能な整数で、範囲は−32768～32767(約3万)。内部表現のサイズは2バイト。

short型で表現可能な最大値32767を超えると16ビット目が1となって負数になる
short型で表現された−1(0bffff)の演算結果がこれを超える場合、17ビット目以上が無視される
符号なしで16ビット目が1となるリテラル(0x8000)以上の数はint型で解釈され、short型へのキャストが必要
- 16ビット目が1のリテラルをshort型にキャストした場合、負数とみなされる

short s = 0;              // 0はそのままshortとして解釈される
System.out.println(s);    // 0

s = 0x7fff;               // short型の正数上限
System.out.println(s);    // 32767
System.out.println(++s);  // short型では負数となり-32768

s = (short)0xffff;        // int型の正数として解釈→キャストが必要
System.out.println(s);    // -1
System.out.println(++s);  // short型の範囲で循環して0

short s = 0; // 0はそのままshortとして解釈される

System.out.println(s); // 0

s = 0x7fff; // short型の正数上限

System.out.println(s); // 32767

System.out.println(++s); // short型では負数となり-32768

s = (short)0xffff; // int型の正数として解釈→キャストが必要

System.out.println(s); // -1

System.out.println(++s); // short型の範囲で循環して0

int

32ビットの符号付き2進数で表現可能な整数で、範囲は−2147483648～2147483647(約21億、10⁹オーダー)。内部表現のサイズは4バイト。

int型で表現可能な最大値2147483647を超えると最上位ビットが1となって負数になる
int型で表現された−1(0bffffffff)の演算結果がこれを超える場合、33ビット目以上が無視される
符号なしで32ビット目が1となるリテラル(0x80000000)以上の数は、そのままint型の負数として解釈される

int i = 0;                // 0はそのままintとして解釈される
System.out.println(i);    // 0

i = 0x7fffffff;           // int型の正数上限
System.out.println(i);    // 2147483647
System.out.println(++i);  // int型では負数となり-2147483648

i = 0xffffffff;            // int型の負数として解釈
System.out.println(i);    // -1
System.out.println(++i);  // int型の範囲で循環して0

int i = 0; // 0はそのままintとして解釈される

System.out.println(i); // 0

i = 0x7fffffff; // int型の正数上限

System.out.println(i); // 2147483647

System.out.println(++i); // int型では負数となり-2147483648

i = 0xffffffff; // int型の負数として解釈

System.out.println(i); // -1

System.out.println(++i); // int型の範囲で循環して0

long

64ビットの符号付き2進数で表現可能な整数で、範囲は−9223372036854775808～9223372036854775807(約920京、10¹⁸オーダー)。内部表現のサイズは8バイト。

与えるリテラルが16ビット以内の数値の場合、int型で解釈され、負数の場合は負数として64ビットに拡張される
与えるリテラルが17ビット以上の数値の場合、リテラルには末尾にL/lを付ける必要がある
与えるリテラルが65ビット以上の数値を扱うことはできない
long型で表現可能な最大値9223372036854775807を超えると最上位ビットが1となって負数になる
long型で表現された−1(0bffffffffffffffff)の演算結果がこれを超える場合、65ビット目以上が無視される

long lng = 0xffffffff;      // 16ビット以内の数はint型で解釈
System.out.println(lng);    // -1
System.out.println(Long.toHexString(lng)); // ffffffffffffffff

lng = 0x100000000L;          // 17ビット以上の数は末尾にL/lをつけないと範囲外エラー
System.out.println(lng);    // 4294967296

lng = 0x7fffffffffffffffL;  // long型の正数上限
System.out.println(lng);    // 9223372036854775807
System.out.println(++lng);  // long型で負数となり-9223372036854775808

lng = 0xffffffffffffffffL;  // long型の負数として解釈
System.out.println(lng);    // -1
System.out.println(++lng);  // long型の範囲で循環して0

// lng = 0x10000000000000000L;
// 65ビット以上の整数は扱えない

long lng = 0xffffffff; // 16ビット以内の数はint型で解釈

System.out.println(lng); // -1

System.out.println(Long.toHexString(lng)); // ffffffffffffffff

lng = 0x100000000L; // 17ビット以上の数は末尾にL/lをつけないと範囲外エラー

System.out.println(lng); // 4294967296

lng = 0x7fffffffffffffffL; // long型の正数上限

System.out.println(lng); // 9223372036854775807

System.out.println(++lng); // long型で負数となり-9223372036854775808

lng = 0xffffffffffffffffL; // long型の負数として解釈

System.out.println(lng); // -1

System.out.println(++lng); // long型の範囲で循環して0

// lng = 0x10000000000000000L;

// 65ビット以上の整数は扱えない

数値型(実数型)

float

32ビット(4バイト)の浮動小数点数で、−3.4028235×10³⁸～−1.4×10⁻⁴⁵、1.4×10⁻⁴⁵～3.4028235×10³⁸の範囲の実数を扱える。

内部表現はIEEE754、符号1ビット、指数部8ビット、仮数部23ビット
最大値はFloat.MAX、最小値はFloat.MINで取得できる
最大値を超える値はInfinity、絶対値が最小値を下回る値は0.0となる

double

64 ビット(8バイト)の浮動小数点数で、−1.7976931348623157×10³⁰⁸～−4.9×10⁻³²⁴、4.9×10⁻³²⁴～1.7976931348623157×10³⁰⁸の範囲の実数を扱える。

内部表現はIEEE754、符号1ビット、指数部11ビット、仮数部52ビット
最大値はDouble.MAX、最小値はDouble.MINで取得できる
最大値を超える値はInfinity、絶対値が最小値を下回る値は0.0となる

文字型

char

16ビットのユニコード1文字を扱う。シングルクォートで囲んだ1文字のほか、ユニコードなら\u0000～\uffff、10進数なら0～65535。

    for (char c = '!'; c <= '~'; c++) {
      System.out.print(c);
    }
    // !"#$%&'()*+,-./0123456789:;<=>?@ABCDEFGHIJKLMNOPQRSTUVWXYZ[\]^_`abcdefghijklmnopqrstuvwxyz{|}~

    System.out.println();
    for (char c = 0x0021; c <= 0x007e; c++) {
      System.out.print(c);
    }
    // !"#$%&'()*+,-./0123456789:;<=>?@ABCDEFGHIJKLMNOPQRSTUVWXYZ[\]^_`abcdefghijklmnopqrstuvwxyz{|}~

    System.out.println();
    for (char c = 'ぁ'; c <= 'ん'; c++) {
      System.out.print(c);
    }
    // ぁあぃいぅうぇえぉおかがきぎくぐけげこごさざしじすずせぜそぞただちぢっつづてでとどなにぬねのはばぱひびぴふぶぷへべぺほぼぽまみむめもゃやゅゆょよらりるれろゎわゐゑをん

    System.out.println();
    for (char c = 0x3041; c <= 0x03093; c++) {
      System.out.print(c);
    }
    // ぁあぃいぅうぇえぉおかがきぎくぐけげこごさざしじすずせぜそぞただちぢっつづてでとどなにぬねのはばぱひびぴふぶぷへべぺほぼぽまみむめもゃやゅゆょよらりるれろゎわゐゑをん

    System.out.println();

for (char c = '!'; c <= '~'; c++) {

System.out.print(c);

}

// !"#$%&'()*+,-./0123456789:;<=>?@ABCDEFGHIJKLMNOPQRSTUVWXYZ[\]^_`abcdefghijklmnopqrstuvwxyz{|}~

System.out.println();

for (char c = 0x0021; c <= 0x007e; c++) {

System.out.print(c);

}

// !"#$%&'()*+,-./0123456789:;<=>?@ABCDEFGHIJKLMNOPQRSTUVWXYZ[\]^_`abcdefghijklmnopqrstuvwxyz{|}~

System.out.println();

for (char c = 'ぁ'; c <= 'ん'; c++) {

System.out.print(c);

}

// ぁあぃいぅうぇえぉおかがきぎくぐけげこごさざしじすずせぜそぞただちぢっつづてでとどなにぬねのはばぱひびぴふぶぷへべぺほぼぽまみむめもゃやゅゆょよらりるれろゎわゐゑをん

System.out.println();

for (char c = 0x3041; c <= 0x03093; c++) {

System.out.print(c);

}

System.out.println();

MySQL – CSVファイルのインポートでエラー

2021-06-01 / tau / 1件のコメント

概要

MySQLでデータベースにCSVファイルをインポートしようとしたときに以下のようなエラーが出た。

mysql> LOAD DATA LOCAL INFILE "~/share/rounds.csv"
    -> INTO TABLE rounds FIELDS TERMINATED BY ',';
ERROR 3948 (42000): Loading local data is disabled; this must be enabled on both the client and server sides

mysql> LOAD DATA LOCAL INFILE "~/share/rounds.csv"

-> INTO TABLE rounds FIELDS TERMINATED BY ',';

ERROR 3948 (42000): Loading local data is disabled; this must be enabled on both the client and server sides

MySQLのバージョンが新しいと出るらしく、メッセージにあるようにサーバーとクライアントの双方で許可を与える必要があるそうだ。

手順

クライアント側の指定

mysqlのログイン時にオプションでローカルの入力ファイルを許可する。オプションの書き方は以下2通りのいずれか

--enable-local-infile
--local_infile=1またはon

$ mysql -u root -p --enable-local-infile

1	$ mysql -u root -p --enable-local-infile

これを設定しておかないと、後述のグローバルパラメーターを有効にしても、LOAD DATA実行時に以下のようなエラーが出る。

ERROR 2068 (HY000): LOAD DATA LOCAL INFILE file request rejected due to restrictions on access.

1	ERROR 2068 (HY000): LOAD DATA LOCAL INFILE file request rejected due to restrictions on access.

サーバー側の指定

MySQLにログイン後、以下のコマンドでサーバーのlocal_infileの設定を確認すると0(無効)になっている。

mysql> select @@local_infile;
+----------------+
| @@local_infile |
+----------------+
|              0 |
+----------------+
1 row in set (0.00 sec)

mysql> select @@local_infile;

+----------------+

| @@local_infile |

+----------------+

| 0 |

+----------------+

1 row in set (0.00 sec)

local_infileを有効にして、設定が反映されていることを確認。

mysql> SET GLOBAL local_infile=on;
Query OK, 0 rows affected (0.00 sec)

mysql> select @@local_infile;
+----------------+
| @@local_infile |
+----------------+
|              1 |
+----------------+
1 row in set (0.00 sec)

mysql> SET GLOBAL local_infile=on;

Query OK, 0 rows affected (0.00 sec)

mysql> select @@local_infile;

+----------------+

| @@local_infile |

+----------------+

| 1 |

+----------------+

1 row in set (0.00 sec)

読み込み成功

mysql> LOAD DATA LOCAL INFILE "~/share/rounds.csv"
    -> INTO TABLE rounds
    -> FIELDS TERMINATED BY ','
    -> LINES TERMINATED BY "\r\n";
Query OK, 1 row affected (0.01 sec)
Records: 1  Deleted: 0  Skipped: 0  Warnings: 0

mysql> LOAD DATA LOCAL INFILE "~/share/rounds.csv"

-> INTO TABLE rounds

-> FIELDS TERMINATED BY ','

-> LINES TERMINATED BY "\r\n";

Query OK, 1 row affected (0.01 sec)

Records: 1 Deleted: 0 Skipped: 0 Warnings: 0

論理演算

2021-05-30 / tau / コメントする

記号定義

以降の議論で以下の様に記号を定義する。

変数Aの否定(not)→ $\overline{A}$
変数AとBの論理積(and)→ $AB$ または $A \cdot B$
変数AとBの論理和(or)→ $A + B$
変数AとBの吐いた論理和(xor)→ $A \oplus B$

基本演算の真理値表

not/and/or

not、and、orの真理値表は以下のとおり。T、FはTrue(真)、False(偽)を表す。

$\begin{align*} \begin{array}{c|c} A & \overline{A} \\ \hline T & F \\ F & T \end{array} \qquad \begin{array}{cc|cc} A & B & AB& A+B \\ \hline T & T & T & T\\ T & F & F & T\\ F & T & F & T\\ F & F & F & F\\ \end{array} \end{align}$

排他論理和(exclusive or)

2つの変数の真偽値が「異なるときに真、同じ時に偽」となる演算。

$\begin{align*} \begin{array}{cc|c} A & B & A \oplus B \\ \hline T & T & F \\ T & F & T \\ F & T & T \\ F & F & F \end{array} \end{align}$

各種法則

基本

(1) $\begin{align*} \overline{\overline{A}} = A ,\quad \begin{array}{c} AA = A \\ A \overline{A} = F \end{array} ,\quad \begin{array}{c} A + A = A \\ A + \overline{A} = T \end{array} \end{align*} \begin{align*} \begin{array}{l} AT =A \\ AF =F \end{array} \quad \begin{array}{l} A + T = T \\ A + F = A \end{array} \end{align*}$

交換法則

(2) $\begin{align*} AB = BA \quad A + B = B + A \end{align*}$

結合法則

(3) $\begin{gather*} (AB)C = A(BC) \\ (A + B) + C = A + (B + C) \end{gather*}$

＜確認＞

$\begin{align*} \begin{array}{ccc|cc|cc} A & B & C & AB & (AB)C & (BC) & A(BC)\\ \hline T & T & T & T &T & T & T\\ T & T & F & T & F & F & F\\ T & F & T & F & F & F & F\\ T & F & F & F & F & F & F\\ F & T & T & F & F & T & F\\ F & T & F & F & F & F & F\\ F & F & T & F & F & F & F\\ F & F & F & F & F & F & F\\ \end{array} \end{align} \begin{align*} \begin{array}{ccc|cc|cc} A & B & C & A+B & (A+B)+C & (B+C) & A+(B+C)\\ \hline T & T & T & T & T & T & T\\ T & T & F & T & T & T & T\\ T & F & T & T & T & T & T\\ T & F & F & T & T & F & T\\ F & T & T & T & T & T & T\\ F & T & F & T & T & T & T\\ F & F & T & F & T & T & T\\ F & F & F & F & F & F & F\\ \end{array} \end{align}$

分配法則

(4) $\begin{align*} A(B + C) = AB + AC \end{align*}$

＜確認＞

$\begin{align*} \begin{array}{ccc|cc|ccc} A & B & C & B+C & A(B+C) & AB & AC & AB+AC\\ \hline\hline T & T & T & T & T & T & T & T\\ T & T & F & T & T & T & F & T\\ T & F & T & T & T & F & T & T\\ T & F & F & F & F & F & F & F\\ F & T & T & T & F & F & F & F\\ F & T & F & T & F & F & F & F\\ F & F & T & F & F & F & F & F\\ F & F & F & F & F & F & F & F\\ \end{array} \end{align}$

ド・モルガンの法則(De Morgan’s laws)

ド・モルガンの法則はandとorの相互変換に関するもので、論理式の変形の基本手順として使われる。

(5) $\begin{align*} \overline{A \cdot B} = \overline{A} + \overline{B} ,\quad \overline{A+B} = \overline{A} \cdot \overline{B} \end{align*}$

＜確認＞

$\begin{align*} \begin{array}{cc|cc|cc|cc} A & B & \overline{A} & \overline{B} & \overline{A \cdot B} & \overline{A} + \overline{B} & \overline{A + B} & \overline{A} \cdot \overline{B} \\ \hline T & T & F & F & F & F & F & F \\ T & F & F & T & T & T & F & F \\ F & T & T & F & T & T & F & F \\ F & F & T & T & T & T &T & T \end{array} \end{align}$

ド・モルガンの法則による式変形

変形の基本

ド・モルガンの法則を利用して論理式を変形していくのに、以下の変形手順が用いられる。

＜否定の否定＞

(6) $\begin{align*} \begin{array}{l} A \cdot B = \overline{\overline{A \cdot B}} = \overline{\overline{A} + \overline{B}} \\ A + B = \overline{\overline{A + B}} = \overline{\overline{A} \cdot \overline{B}} \\ \end{array} \end{align*}$

＜Falseとのor＞

(7) $\begin{align*} A \cdot \overline{B} = A \cdot \overline{B} + A \cdot \overline{A} = A (\overline{B} + \overline{A}) \end{align*}$

NANDゲート化

NANDゲートは、A、B2つの入力のandのnotを出力するゲートで、任意の論理回路をNANDゲートの組み合わせで実装できる(完全性：completeness)。

例えばnot、and、or、xorの基本演算を、ド・モルガンの低利で変形してNANDゲートのみで表してみる。

(8) $\begin{gather*} \overline{A} = \overline{A \cdot A} \\ A \cdot B = \overline{\overline{A \cdot B}} \\ A + B = \overline{\overline{A + B}} = \overline{\overline{A} \cdot \overline{B}} \end{gather*}$

これらをゲート図で表すと以下のようになる。

真偽表の変換

変換の考え方

排他論理和(XOR)の演算をNANDゲートで構成することを考える。AとBに対するTrue、Falseの組み合わせのうち結果がTrueとなるものだけを抜き出すと、(A, B) = (T, F), (F, T)。それぞれの入力に対して結果がTrueとなるためには以下のいずれか満たされる必要がある。

(9) $\begin{equation*} \left\{ \begin{array}{l} A \cdot \overline{B} = T \\ \overline{A} \cdot B = T \end{array} \end{equation*}$

これらのいずれかが成立すれば(左辺の論理和を取れば)Trueの結果となり、Falseとなる結果は論理和をとっても変わらないので、XORの出力は以下のように表現される。

(10) $\begin{equation*} A \oplus B = A \cdot \overline{B} +\overline{A} \cdot B \end{equation*}$

この式に真偽値表の組み合わせを入れると、XORの結果になることが確認できる。

NANDゲートへの変換1

この式をド・モルガンの定理を使って変形すると以下のようになる。

(11) $\begin{align*} A \cdot \overline{B} +\overline{A} \cdot B &= \overline{\overline{A \cdot \overline{B} +\overline{A} \cdot B}} \\ &= \overline{ \overline{A \cdot \overline{B}} \cdot \overline{\overline{A} \cdot B}} \end{align*}$

真理値表の確認。

$\begin{gather*} \begin{array}{cc|cc|cc|c} A & B & \overline{A} & \overline{B} & \overline{A \cdot \overline{B}} & \overline{\overline{A} \cdot B} & \overline{ \overline{A \cdot \overline{B}} \cdot \overline{\overline{A} \cdot B}}\\ \hline T & T & F & F & T & T & F \\ T & F & F & T & F & T & T \\ F & T & T & F & T & F & T \\ F & F & T & T & T & T & F \end{array} \end{gather}$

式(11)をNANDゲートによる回路図で表すと以下の通り。2つのNOTはNANDゲートで作ることができ、5つのNANDゲートを使う。

NANDゲートへの変換2

一方、式(11)の2つのNANDの中を以下のように変形する。

(12) $\begin{align*} A \cdot \overline{B} &= A \cdot \overline{B} + A \cdot \overline{A} = A \cdot (\overline{A} + \overline{B}) = A \cdot \overline{A \cdot B} \\ \overline{A} \cdot B &= \overline{B} \cdot B + \overline{A} \cdot B = (\overline{A} + \overline{B}) \cdot B = \overline{A \cdot B} \cdot B \end{align*}$

これらにより、XORは以下のようにも表せる。

(13) $\begin{align*} A \cdot \overline{B} +\overline{A} \cdot B &= \overline{ \overline{A \cdot \overline{B}} \cdot \overline{\overline{A} \cdot B}} \\ &= \overline{\overline{A \cdot \overline{A \cdot B}} \cdot \overline{\overline{A \cdot B} \cdot B}} \end{align*}$

式(12)をNANDゲートによる回路図で表すと以下の通り。式(11)の場合に比べてNANDゲートが4つですむ。

Rails – ページネーション～kaminari

2021-04-18 / tau / コメントする

概要

Gemのkaminariを利用してページネーションを実装する手順。最も基本的な手順は以下の通り。

kaminariをインストールする
コントローラーにpageメソッドを記述
ビューにpaginateメソッドを記述

基本手順

kaminariのインストール

Gemfileに以下の1行を追加し、bundle install

gem 'kaminari'

1	gem 'kaminari'

準備

ダミーデータの準備

200個のPostデータをページネートすることとし、seeds.rbで初期データを生成する。

標準の表示

コントローラー

class PostsController < ApplicationController
    def kaminari
      @posts = Post.all.order(id: "desc")
    end
end

class PostsController < ApplicationController

def kaminari

@posts = Post.all.order(id: "desc")

end

ビュー

<h1>kaminari test</h1>

<% @posts.each do |post| %>
  <p><%= post.id %> : <%= post.comment %></p>
<% end %>

<h1>kaminari test</h1>

<% @posts.each do |post| %>

<% end %>

この状態だと、200個の投稿データが全て表示され、スクロールしなければならなくなる。

ページネーションの追加

コントローラーで、表示するモデルデータにpageメソッドとperメソッドを追加。

kaminariによってparamsにビューで表示しているページが追加される
pageに引数として表示させるページを渡す
perで1ページあたりの表示数を指定する

class PostsController < ApplicationController
    def kaminari
      @posts = Post.all.order(id: "desc").page(params[:page]).per(20)
    end
end

class PostsController < ApplicationController

def kaminari

@posts = Post.all.order(id: "desc").page(params[:page]).per(20)

end

ビューにpagenateメソッドを追加し、ページ操作の表示をさせる。

<h1>kaminari test</h1>

<%= paginate @posts %>

<% @posts.each do |post| %>
  <p><%= post.id %> : <%= post.comment %></p>
<% end %>

<h1>kaminari test</h1>

<%= paginate @posts %>

<% @posts.each do |post| %>

<% end %>

Rails – データベースの初期データ

2021-04-17 / tau / コメントする

概要

Railsで準備されているseeds.rbファイルを使って、データベースの初期データを準備する手順。

Railsであらかじめdbディレクトリー下にseeds.rbファイルが準備されている。

# This file should contain all the record creation needed to seed the database with its default values.
# The data can then be loaded with the rails db:seed command (or created alongside the database with db:setup).
#
# Examples:
#
#   movies = Movie.create([{ name: 'Star Wars' }, { name: 'Lord of the Rings' }])
#   Character.create(name: 'Luke', movie: movies.first)

# This file should contain all the record creation needed to seed the database with its default values.

# The data can then be loaded with the rails db:seed command (or created alongside the database with db:setup).

# Examples:

# movies = Movie.create([{ name: 'Star Wars' }, { name: 'Lord of the Rings' }])

# Character.create(name: 'Luke', movie: movies.first)

このファイルに初期データをセットするコードを書き、コンソールでrails db:seedを実行すると、そのコードが実行される。

操作例

たとえばPostモデルで200件のダミーデータを準備する場合。

Postモデル

commentフィールドだけを持つPostモデルを準備する。

class CreatePosts < ActiveRecord::Migration[5.1]
  def change
    create_table :posts do |t|
      t.string :comment

      t.timestamps
    end
  end
end

class CreatePosts < ActiveRecord::Migration[5.1]

def change

create_table :posts do |t|

t.string :comment

t.timestamps

end

seeds.rbファイル

seeds.rbファイルに、200個のPostデータを書き込むコードを書く。

db/seeds.rb

200.times do |i|
  Post.create(comment:"#{i}番目の投稿")
end

200.times do |i|

Post.create(comment:"#{i}番目の投稿")

end

Railsコマンド実行

以下のRailsコマンドでseeds.rbファイルを実行し、データベースにデータを書き込む。

[vagrant@vagrant gem_test]$ rails db:seed

1	[vagrant@vagrant gem_test]$ rails db:seed

結果

以下のとおりデータが書き込まれる。

mysql> select * from posts;
+-----+--------------------+---------------------+---------------------+
| id  | comment            | created_at          | updated_at          |
+-----+--------------------+---------------------+---------------------+
|   1 | 0番目の投稿        | 2021-04-17 02:34:36 | 2021-04-17 02:34:36 |
|   2 | 1番目の投稿        | 2021-04-17 02:34:36 | 2021-04-17 02:34:36 |
|   3 | 2番目の投稿        | 2021-04-17 02:34:36 | 2021-04-17 02:34:36 |
|   4 | 3番目の投稿        | 2021-04-17 02:34:36 | 2021-04-17 02:34:36 |
|   5 | 4番目の投稿        | 2021-04-17 02:34:36 | 2021-04-17 02:34:36 |

.....

| 196 | 195番目の投稿      | 2021-04-17 02:34:36 | 2021-04-17 02:34:36 |
| 197 | 196番目の投稿      | 2021-04-17 02:34:37 | 2021-04-17 02:34:37 |
| 198 | 197番目の投稿      | 2021-04-17 02:34:37 | 2021-04-17 02:34:37 |
| 199 | 198番目の投稿      | 2021-04-17 02:34:37 | 2021-04-17 02:34:37 |
| 200 | 199番目の投稿      | 2021-04-17 02:34:37 | 2021-04-17 02:34:37 |
+-----+--------------------+---------------------+---------------------+
200 rows in set (0.00 sec)

mysql> select * from posts;

+-----+--------------------+---------------------+---------------------+

+-----+--------------------+---------------------+---------------------+

| 1 | 0番目の投稿 | 2021-04-17 02:34:36 | 2021-04-17 02:34:36 |

| 2 | 1番目の投稿 | 2021-04-17 02:34:36 | 2021-04-17 02:34:36 |

| 3 | 2番目の投稿 | 2021-04-17 02:34:36 | 2021-04-17 02:34:36 |

| 4 | 3番目の投稿 | 2021-04-17 02:34:36 | 2021-04-17 02:34:36 |

| 5 | 4番目の投稿 | 2021-04-17 02:34:36 | 2021-04-17 02:34:36 |

.....

| 196 | 195番目の投稿 | 2021-04-17 02:34:36 | 2021-04-17 02:34:36 |

| 197 | 196番目の投稿 | 2021-04-17 02:34:37 | 2021-04-17 02:34:37 |

| 198 | 197番目の投稿 | 2021-04-17 02:34:37 | 2021-04-17 02:34:37 |

| 199 | 198番目の投稿 | 2021-04-17 02:34:37 | 2021-04-17 02:34:37 |

| 200 | 199番目の投稿 | 2021-04-17 02:34:37 | 2021-04-17 02:34:37 |

+-----+--------------------+---------------------+---------------------+

200 rows in set (0.00 sec)