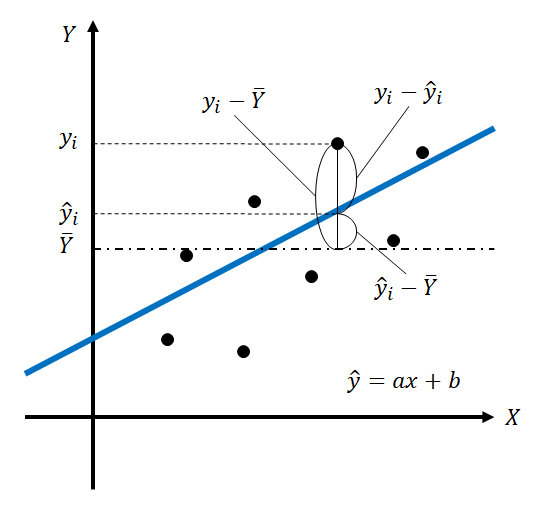
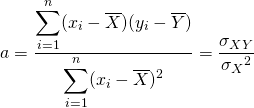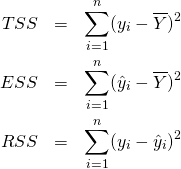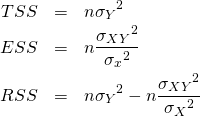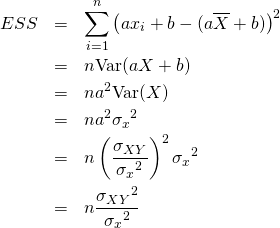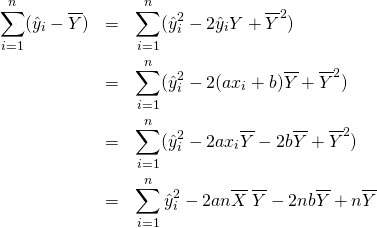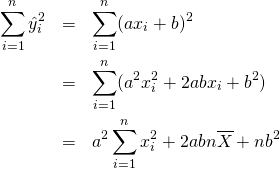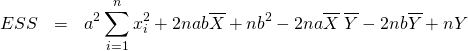要素に対するスカラー演算
配列の要素に対するスカラー演算は、それぞれの要素に作用。
|
1 2 3 4 5 6 7 8 9 10 |
v = np.array([1, 2, 3]) print(v + 1) print(v - 1) print(v * 2) print(v / 2) # [2 3 4] # [0 1 2] # [2 4 6] # [0.5 1. 1.5] |
二次元配列も同じ。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
m = np.array([[1, 2, 3], [4, 5, 6]]) print(m1 + 1) print(m1 - 1) print(m1 * 2) print(m1 / 2) # [[2 3 4] # [5 6 7]] # [[0 1 2] # [3 4 5]] # [[ 2 4 6] # [ 8 10 12]] # [[0.5 1. 1.5] # [2. 2.5 3. ]] |
なお、配列が後ろに来ても要素ごとに演算。
|
1 2 3 4 5 6 |
v = np.array([1, 2, 3]) print(1 - v) print(2 / v) # [ 0 -1 -2] # [2. 1. 0.66666667] |
要素ごとの演算
同じ形状の配列同士の演算は、それぞれの要素ごとの演算。
|
1 2 3 4 5 6 7 8 9 10 11 |
v1 = np.array([1, 2, 3]) v2 = np.array([4, 5, 6]) print(v2 + v1) print(v2 - v1) print(v2 * v1) print(v2 / v1) # [5 7 9] # [3 3 3] # [ 4 10 18] # [4. 2.5 2. ] |
要素ごとの比較
配列同士の比較は、要素ごとの比較結果の配列。
|
1 2 3 4 5 6 7 |
v1 = np.array([0, 1, 2, 3]) v2 = np.array([0, 2, 2, 0]) print(v1 == v2) print(v1 > v2) # [ True False True False] # [False False False True] |
関数演算
numpyの関数の引数が配列の場合、要素ごとの演算結果となる。
|
1 2 3 4 5 6 |
v = np.array([1, 2, 3]) print(np.sqrt(v)) print(np.log(v)) # [1. 1.41421356 1.73205081] # [0. 0.69314718 1.09861229] |
![Rendered by QuickLaTeX.com \begin{equation*} \left[ \begin{array}{c} a \\ b \end{array} \right] = \left[ \begin{array}{c} \dfrac{n S_{xy} - S_x S_y}{n S_{xx} - {S_x}^2} \\ \dfrac{S_{xx} S_y - S_x S_{xy}}{n S_{xx} - {S_x}^2} \end{array} \right] \end{equation*}](http://taustation.com/wp1/wp-content/ql-cache/quicklatex.com-5ab9943a0ccf9c81304d639401e154d8_l3.png)