概要
![]() のデータからなる複数の標本に対して、線形式で最も説明性の高いものを求める。
のデータからなる複数の標本に対して、線形式で最も説明性の高いものを求める。
そのために、各データの![]() に線形式を適用して得られた値
に線形式を適用して得られた値![]() と
と![]() の差(残差)の平方和が最小となるような係数
の差(残差)の平方和が最小となるような係数![]() を求める(最小二乗法)。
を求める(最小二乗法)。
定式化
(1) 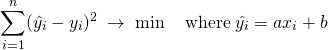
ここで残差を最小化する![]() を求めるために、それぞれで偏微分する。
を求めるために、それぞれで偏微分する。
(2) 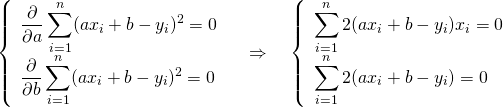
展開して
(3) 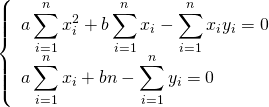
各和の記号を新たに定義し、行列表示で表すと、
(4) ![]()
回帰式の係数
式(4)を解くと以下を得る。
(5) ![Rendered by QuickLaTeX.com \begin{equation*} \left[ \begin{array}{c} a \\ b \end{array} \right] = \left[ \begin{array}{c} \dfrac{n S_{xy} - S_x S_y}{n S_{xx} - {S_x}^2} \\ \dfrac{S_{xx} S_y - S_x S_{xy}}{n S_{xx} - {S_x}^2} \end{array} \right] \end{equation*}](http://taustation.com/wp1/wp-content/ql-cache/quicklatex.com-5ab9943a0ccf9c81304d639401e154d8_l3.png)
あるいは式(5)については以下のようにも表せる。ただし以下の式で、![]() 、
、![]()
(6) 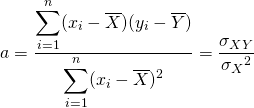
(7) ![]()
決定係数
全変動・回帰変動・残差変動
![]() の回帰式による推定値を
の回帰式による推定値を![]() で表す。
で表す。
ここで、![]() によって、以下の変動が定義される。
によって、以下の変動が定義される。
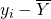
- 全変動。平均からのデータのばらつき。
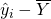
- 回帰変動。平均からのばらつきのうち、回帰式によって説明される部分。
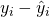
- 残差変動。平均からのばらつきのうち、回帰式によって説明されない部分。
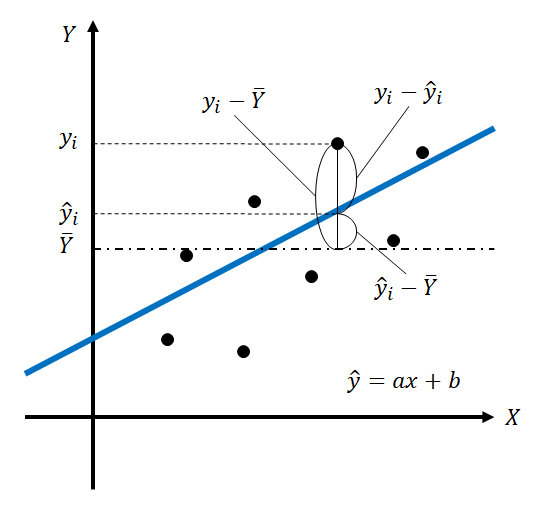
当然、[全変動]=[回帰変動]+[残差変動]となることはすぐに確認できる。
また、これら3つの変動の2乗和をTSS(Total Sum of Squares)、ESS(Explained Sum of Squares、RSS(Residual Sum of Squares)として、以下のように定義する。
(8) 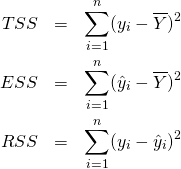
このとき、それぞれについて以下のように表せる。
(9) 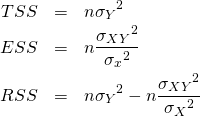
これらから、全変動・回帰変動・残差変動の2乗和についても、以下の関係が成り立つことがわかる。
(10) ![]()
補足~ESS
式(9) のESSの確認。以下のように、線形変換された分散から導ける。
(11) 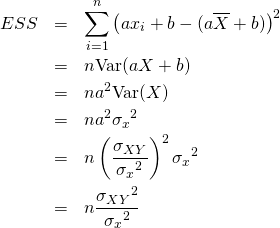
あるいは、以下のように地道に計算しても確認できる。
(12) 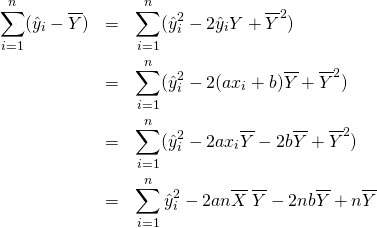
ここで
(13) 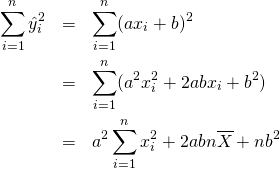
これを代入して、
(14) 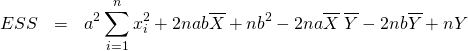
さらに![]() を考慮して、
を考慮して、
(15) 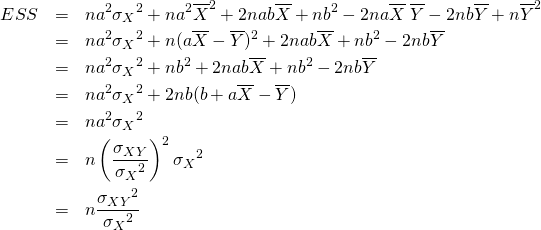
補足~RSS
式(9) のRSSの確認。
(16) 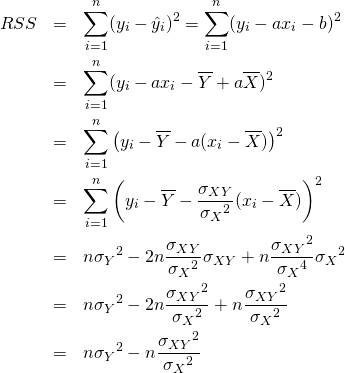
決定係数
決定係数は、全変動のうち回帰変動でどれだけ説明できるか(残差変動が少ないか)を表したもので、通常![]() で表される。
で表される。
(17) ![]()
この値は、残差変動が小さいほど1に近づき、![]() すなわち全変動が回帰変動で全く説明できないときに0となる。
すなわち全変動が回帰変動で全く説明できないときに0となる。