概要
ベイズの定理で典型例として説明される問題。ある病気の検査で陽性が出た場合に罹患している確率を求める。類似の問題として、鉱脈を探るのに試掘結果から鉱脈が存在する確率を求める問題がある。
ロジックとしては、「誤判定の可能性がある調査・検査の結果から、目的とする事実の確率を求める」という構図で共通している。
難病問題
病気の検査の問題を例示する。
ある難病の検査結果が陽性だったとき、その病気に罹患している確率を求めよ。ただし以下の情報が与えられている。
- その難病は1000人に1人が罹患している
- その難病にかかっている場合、90%の確率で検査結果は陽性になる
- その難病にかかっていなくても、20%の確率で検査結果は陽性になる
ここで以下の記号を定義する。
- 全体としての難病の罹患率→
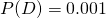
- 難病にかかっている場合に陽性になる確率→
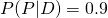
- 難病にかかっていない場合に陽性になる確率→
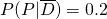
このとき、ベイズの定理により以下の確率を得る。
(1) 
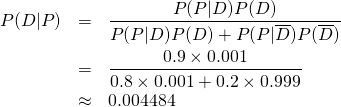
検査結果が陽性であっても、この難病にかかっている確率は0.5%未満ということになる。検査しなければ1000人に1人の罹患率なので0.1%なので、検査によってその確からしさが約4.5倍となるが、事前確率が小さい場合、検査の精度を上げても劇的な判定効果は望めない。
なお、この約4.5倍という値は
に相当し、事前確率
の値が小さいほど4.5に近づく(ベイズの定理の解釈参照)。
なお、2020年、世界的に大きな影響を及ぼしたCOVID-19（新型コロナウイルス）のPCR検査を題材にした記事をこちらにまとめている。