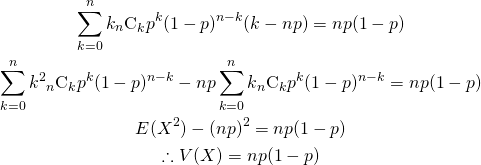概要
二項分布![]() の平均と分散は以下のようになる。
の平均と分散は以下のようになる。
(1) ![]()
これらを導くのに、有用なテクニックを使っているのでまとめておく。
直接定義式から導く方法
この方法は、平均、分散の定義式から直接導いていく過程で、意図的に二項展開の形に持ち込んでいく方法。
平均
平均の定義から、以下のように変形していく。
(2) 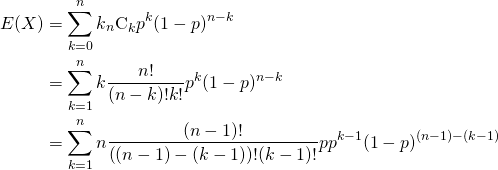
上式では、各項に![]() が乗じられていることから、以下の流れで変形している。
が乗じられていることから、以下の流れで変形している。
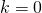 のとき1番目の項はゼロとなるので、和の開始値を
のとき1番目の項はゼロとなるので、和の開始値を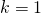 とする
とする- 分子にある
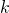 を使って、
を使って、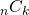 の分母において
の分母において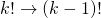 とする
とする - これに整合させるため、分母において
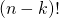 を
を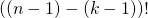 と変形
と変形 - さらに組み合わせの式に整合させるため分子を
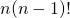 と変形し、最終的に
と変形し、最終的に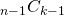 を引き出している。
を引き出している。 - 後に二項定理を使うため、
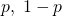 の指数も調整している
の指数も調整している
ここで![]() とおくと、カウンターの範囲は
とおくと、カウンターの範囲は![]() から
から![]() となることから、
となることから、
(3) 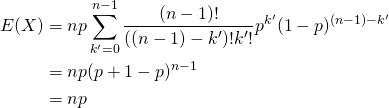
上式では、変形した和の部分が二項展開の形になっていることを利用している。
分散
分散については、![]() が各項に乗じられるが、これを
が各項に乗じられるが、これを![]() と変形して、階乗のランクを下げるところがミソ。
と変形して、階乗のランクを下げるところがミソ。
(4) ![Rendered by QuickLaTeX.com \begin{alignat*}{1} V(X) &= E(X^2) - [E(X)]^2 \\ &= \sum_{k=0}^n k^2 {}_n C_k p^k (1-p)^{n-k} - (np)^2 \\ &= \sum_{k=0}^n \left( k(k-1) + k \right) {}_n C_k p^k (1-p)^{n-k} - (np)^2 \\ &= \sum_{k=2}^n k(k-1) {}_n C_k p^k (1-p)^{n-k} + \sum_{k=1}^n k {}_n C_k p^k (1-p)^{n-k} - (np)^2 \\ \end{alignat*}](http://taustation.com/wp1/wp-content/ql-cache/quicklatex.com-443e6acf6b414d16761dcd5f2a012a8d_l3.png)
上式で、1項目は![]() が乗じられているのでカウンターを
が乗じられているのでカウンターを![]() から、2項目は同じく
から、2項目は同じく![]() からとしている。
からとしている。
ここで1項目について![]() と置いて、平均の時と同じ考え方で以下のように変形。
と置いて、平均の時と同じ考え方で以下のように変形。
(5) 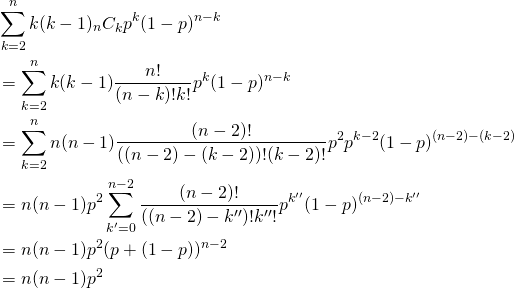
2項目については、![]() とおいて、
とおいて、
(6) 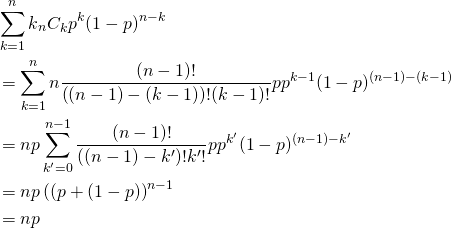
以上を併せて、
(7) ![]()
微分による方法
この方法は、![]() の形に着目して、全事象の式を微分する方法。式展開が素直であり、平均の式を微分した結果がそのまま分散の式になってしまうところが美しい。
の形に着目して、全事象の式を微分する方法。式展開が素直であり、平均の式を微分した結果がそのまま分散の式になってしまうところが美しい。
平均
二項分布の全確率の和は1となる。
(8) 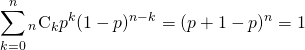
この式の両辺を![]() で微分する。
で微分する。
(9) 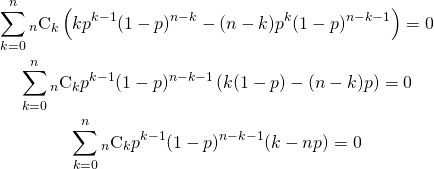
両辺に![]() をかける。
をかける。
(10) 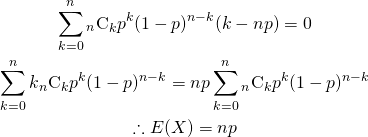
分散
式(10)をもう一度![]() で微分する。
で微分する。
(11) 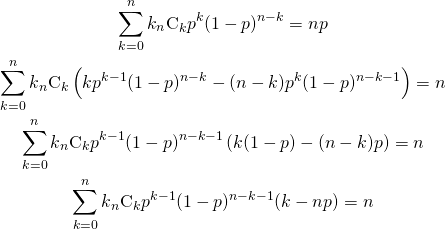
両辺に![]() をかける。
をかける。
(12)