概要
単回帰が![]() への線形関係を扱うのに対して、重回帰は複数の説明変数
への線形関係を扱うのに対して、重回帰は複数の説明変数![]() と
と![]() の線形関係を扱う。
の線形関係を扱う。
データ![]() に対して以下の線形式で最も説明性の高いものを求める。
に対して以下の線形式で最も説明性の高いものを求める。
(1) ![]()
そのために、データとその推測値の残差![]() の平方和が最小となるような係数
の平方和が最小となるような係数![]() を最小二乗法により求める。
を最小二乗法により求める。
定式化
説明変数とターゲットのデータセット![]() 組が次のように得られているとする。
組が次のように得られているとする。
(2) ![]()
残差の平方和については
(3) 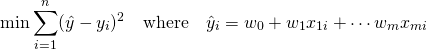
ここで残差を最小化する![]() を求めるために、それぞれで偏微分する。
を求めるために、それぞれで偏微分する。
(4) 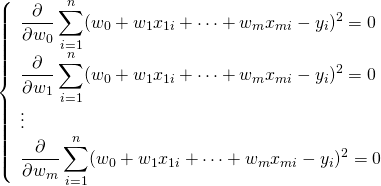
変形すると、
(5) 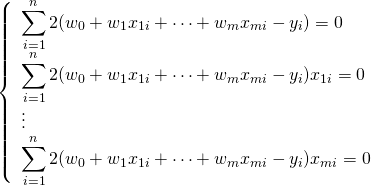
更にこれを展開するのに、![]() ,
, ![]() ,
, ![]() ,
, ![]() とおいて
とおいて
(6) 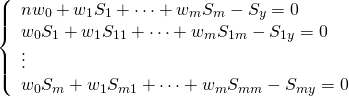
これを行列形式で表示すると
(7) 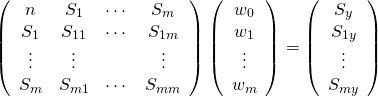
解の導出
式(7)の連立方程式を解けば各係数を得ることができる。ここで左辺の係数行列は以下のようにも表せる。
(8) 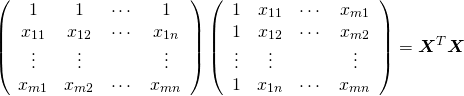
また右辺は次のように表せる。
(9) 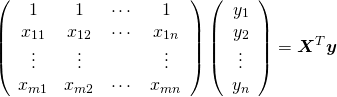
したがって式(7)は以下のように表せる。
(10) ![]()
これを解くと
(11) ![]()
ベクトル・行列による表現と解
定式化の段階からベクトル・行列を用いてみる。式(1)の各変数を全てベクトル形式で表すと以下のようになる。
(12) ![]()
ここで、
(13) 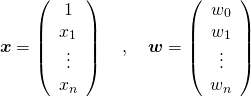
複数データからなるデータセットに対して、式(8)の行列表現を用いると、以下のように表現できる。
(14) ![]()
各データの残差については以下のようになる。
(15) ![]()
ここで残差の二乗和を損失関数Lとして、これを行列で表現すると以下のようになる。
(16) 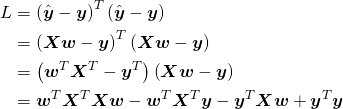
上式の第2項、第3項については以下のように整理できる。
(17) ![]()
損失関数Lはスカラーであり、これを最小にするためにベクトルwで微分し、それらの値がゼロとなるような方程式とする。
(18) ![]()
なお第1項については、式(7)と式(8)より![]() は対象行列なので転置しても同じ行列となり、行列の微分の公式から以下のようになることを利用している。
は対象行列なので転置しても同じ行列となり、行列の微分の公式から以下のようになることを利用している。
(19) ![]()
式(18)をwについて解いて以下を得る。
(20) ![]()
多重共線性
式(7)から![]() を消去する。
を消去する。
(21) 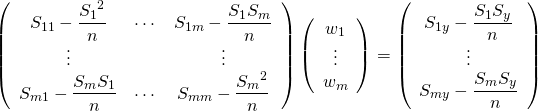
これを分散・共分散で表すと以下の通り。ただし以下で![]() 、
、![]() と表している。
と表している。
(22) 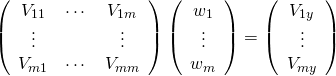
ここで![]() と2つの間に完全な線形関係がある場合、分散・共分散の性質から以下の関係が成り立つ。
と2つの間に完全な線形関係がある場合、分散・共分散の性質から以下の関係が成り立つ。
(23) ![]()
これらを式(22)の係数行列に適用すると、
(24) ![Rendered by QuickLaTeX.com \begin{align*} &\left[ \begin{array}{ccccccc} V_{11} & \cdots & V_{1i} & \cdots & V_{1j} & \cdots & V_{1m}\\ \vdots && \vdots && \vdots && \vdots\\ V_{i1} & \cdots & V_{ii} & \cdots & V_{ij} & \cdots & V_{im}\\ \vdots && \vdots && \vdots && \vdots\\ V_{j1} & \cdots & V_{ji} & \cdots & V_{jj} & \cdots & V_{jm}\\ \vdots && \vdots && \vdots && \vdots\\ V_{m1} & \cdots & V_{mi} & \cdots & V_{mj} & \cdots & V_{mm} \end{array} \right]\\ &= \left[ \begin{array}{ccccccc} V_{11} & \cdots & V_{1i} & \cdots & aV_{1i} & \cdots & V_{1m}\\ \vdots && \vdots && \vdots && \vdots\\ V_{i1} & \cdots & V_{ii} & \cdots & aV_{ii} & \cdots & V_{im}\\ \vdots && \vdots && \vdots && \vdots\\ aV_{i1} & \cdots & aV_{ii} & \cdots & a^2V_{ii} & \cdots & aV_{im}\\ \vdots && \vdots && \vdots && \vdots\\ V_{m1} & \cdots & V_{mi} & \cdots & aV_{mi} & \cdots & V_{mm} \end{array} \right] \end{align*}](http://taustation.com/wp1/wp-content/ql-cache/quicklatex.com-933b818b8ef3c6cf4b6a70d1805f71a8_l3.png)
係数行列の行(列)が一次従属となっていて、その行列式がゼロとなることから、連立方程式は解を持たない。変数間の関係が線形でなくても相関がかなり高い場合は行列式がゼロに近づき、解が不安定になる。