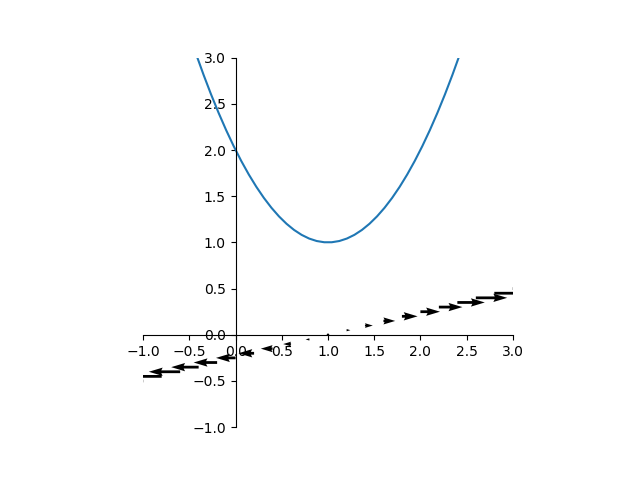
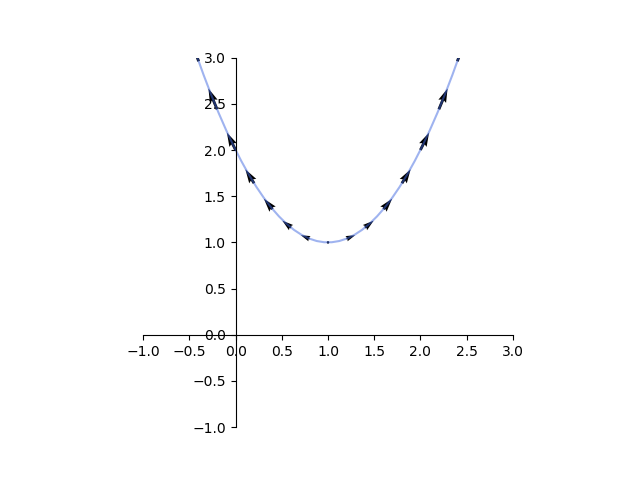
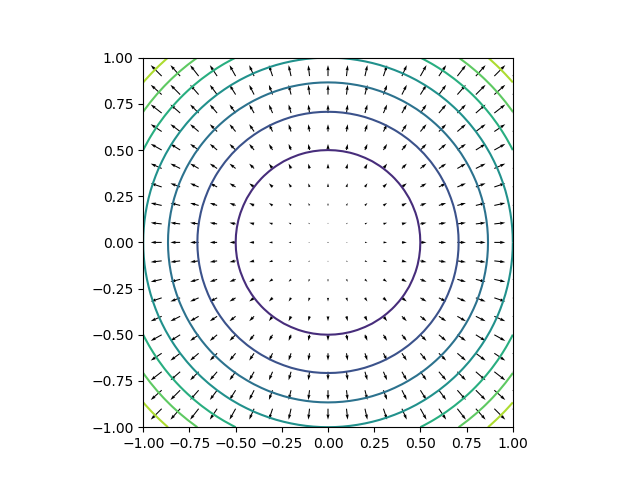
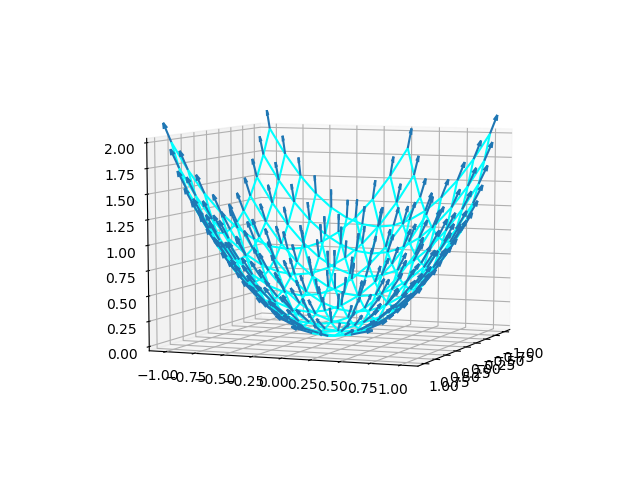
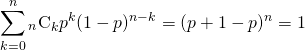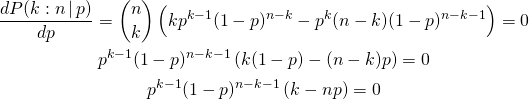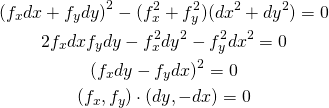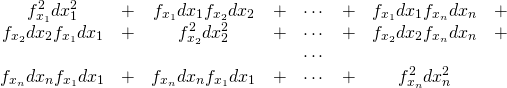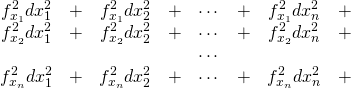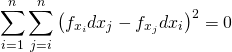概要
不等式制約条件を持つLagrangeの未定乗数法は以下のように表示される(等式条件の場合はこちらを参照)。
(1) ![]()
この場合、停留点が制約条件の範囲外にあれば等式条件と同じ問題となり、範囲内にあれば制約条件なしの通常の極値問題となる。
例題
停留点が制約条件の範囲内の場合
停留点が制約条件の境界内にある次のような問題を考える。
(2) 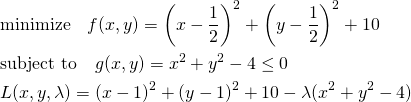
この問題を解くのに、まず停留点が制約条件の範囲内にあるかをチェックする。上の式で![]() と置いて最適化問題を解く。
と置いて最適化問題を解く。
(3) 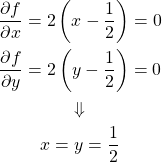
上記の解は制約条件![]() を満足する。この停留点が極値だということが分かっていれば、これが問題の解ということになる。
を満足する。この停留点が極値だということが分かっていれば、これが問題の解ということになる。
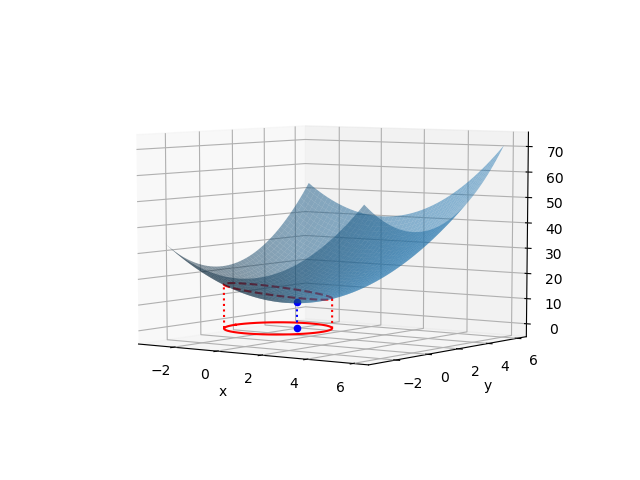
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 |
import numpy as np import matplotlib.pyplot as plt from mpl_toolkits.mplot3d import Axes3D def f(x, y, a, b): return (x - a)**2 + (y - b)**2 + 10 a, b = 1/2, 1/2 x = np.linspace(-3, 6) y = np.linspace(-3, 6) x, y = np.meshgrid(x, y) t = np.linspace(-np.pi, np.pi) xg = 2 * np.cos(t) yg = 2 * np.sin(t) x4min = 6 / np.sqrt(13) y4min = 4 / np.sqrt(13) fmin = f(x4min, y4min, a, b) x4max = - 6 / np.sqrt(13) y4max = - 4 / np.sqrt(13) fmax = f(x4max, y4max, a, b) fig = plt.figure() ax = fig.add_subplot(111, projection='3d') ax.plot_surface(x, y, f(x, y, a, b), alpha=0.5) ax.plot(xg, yg, 0, c='r') ax.plot(xg, yg, f(xg, yg, a, b), c='r', linestyle='dashed') ax.scatter(a, b, 10, c='b') ax.scatter(a, b, 0, c='b') ax.plot([a, a], [b, b], [0, 10], c='b', linestyle='dotted') ax.plot([x4min, x4min], [y4min, y4min], [0, fmin], c='r', linestyle='dotted') ax.plot([x4max, x4max], [y4max, y4max], [0, fmax], c='r', linestyle='dotted') ax.set_xlabel("x") ax.set_ylabel("y") print("f_max={:8.4f}, for x={:7.4f}, y={:7.4f}".format(fmax, x4max, y4max)) print("f_min={:8.4f}, for x={:7.4f}, y={:7.4f}".format(fmin, x4min, y4min)) plt.show() |
停留点が制約条件の範囲外の場合
今度は目的関数の停留点が制約条件の境界の範囲外にある問題を考えてみる。
(4) 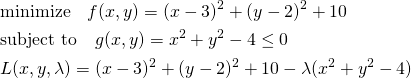
まず停留点が境界条件の範囲内にあるとして、![]() として問題を解いてみる。
として問題を解いてみる。
(5) 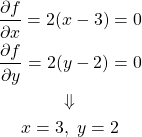
ところがこの解は制約条件![]() を満足しない。解は制約条件の境界上にあることになるので、
を満足しない。解は制約条件の境界上にあることになるので、![]() の条件でLagrangeの未定乗数法によって解く。
の条件でLagrangeの未定乗数法によって解く。
(6) 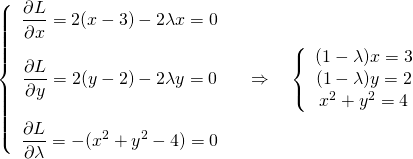
![]() として、
として、
(7) 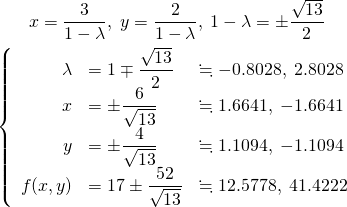
いずれの解も制約条件![]() を満たしており、このうち最小値となる解と目的関数の値は以下の通り。
を満たしており、このうち最小値となる解と目的関数の値は以下の通り。
(8) ![]()
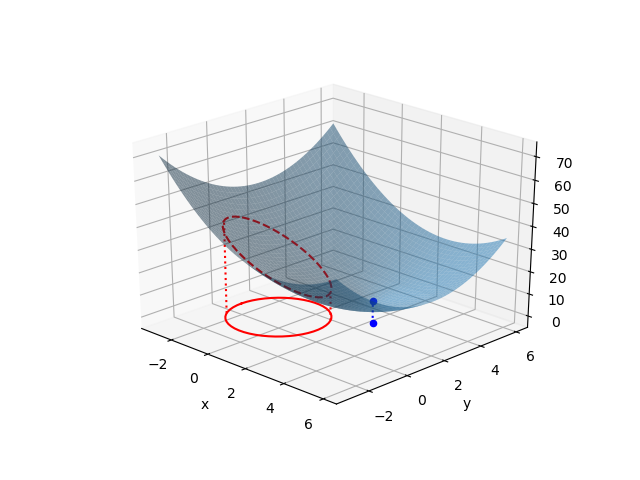
λの符号について
有界でない例
以下、制約条件が![]() で有界でない場合を考える。
で有界でない場合を考える。
最小化問題でgradientが逆向き(極値が制約条件外)
まず、目的関数を最小化する場合を考える。以下の問題では目的関数fの極値が制約条件の範囲外にあり、fとgのgradientがgの境界上で逆向きになる。
(9) 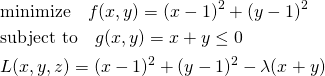
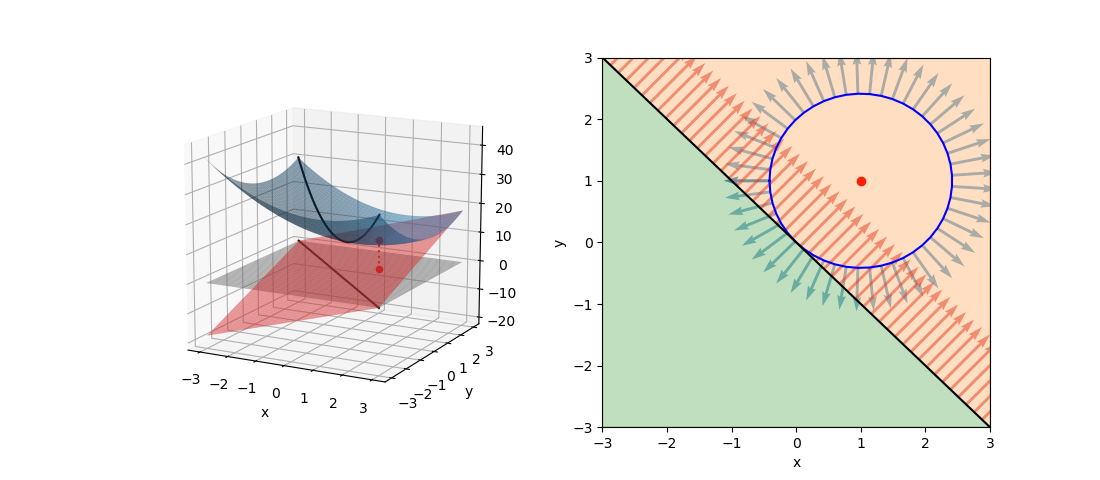
停留点は制約条件の境界上となることから、λ≠0として未定乗数法で解いて以下を得る。λ<0となり、gradientが逆向きであることが現れている(∇f = λ∇g)。
(10) ![]()
最小化問題でgradientが同じ向き(極値が制約条件内)
次の問題では極値が制約条件の範囲内にあり、fとgのgradientがgの境界上で同じ向きとなる。
(11) 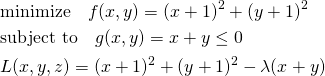
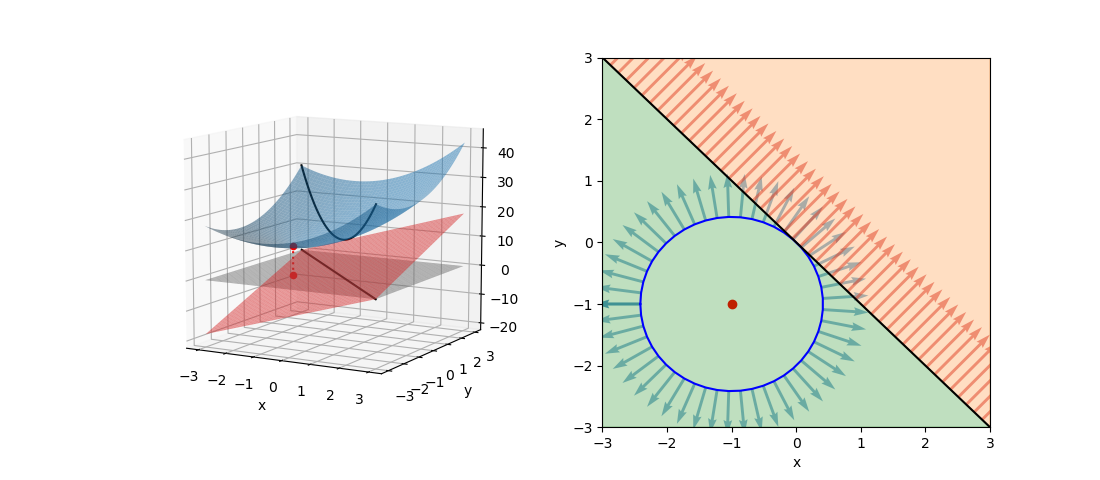
この場合、fの極値は制約条件(緑色)の範囲内にあり、fとgのgradientがgの境界上で同じ向きになる。停留点は制約条件内にあることから、λ=0として制約条件の効果をなくし、単純にfの極値問題を解いて以下を得る(∇f =0)。
(12) ![]()
最大化問題でgradientが同じ向き(極値が制約条件範囲外)
次に目的関数を最大化する場合を考える。以下の問題では目的関数fの極値が制約条件の範囲外にあり、fとgのgradientがgの境界上で同じ向きになる。
(13) 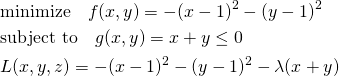
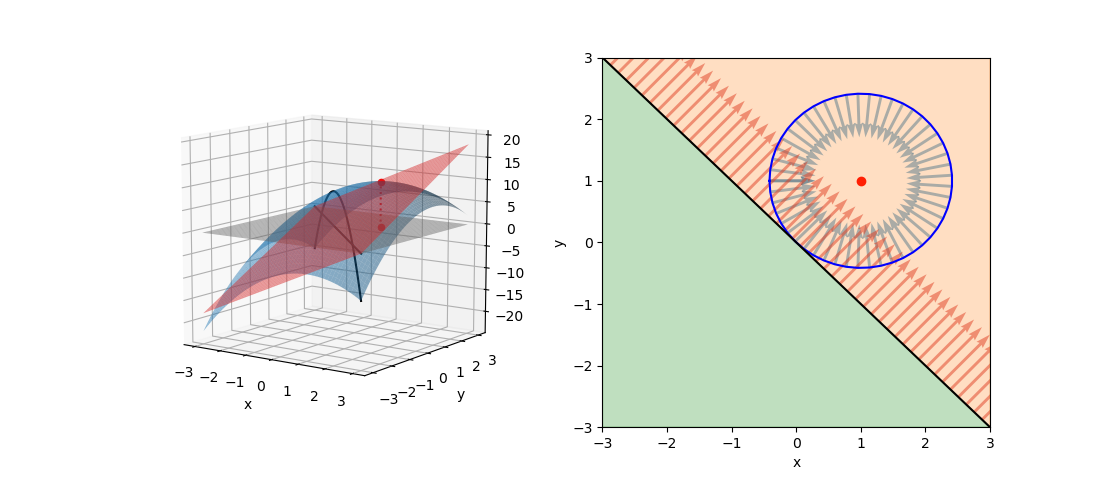
停留点は制約条件の境界上となることから、λ≠0として未定乗数法で解いて以下を得る。λ>0となり、gradientが同じ向きであることが現れている(∇f = λ∇g)。
(14) ![]()
最大化問題でgradientが逆向き(極値が制約条件範囲内)
次の問題では極値が制約条件の範囲内にあり、fとgのgradientがgの境界上で逆向きとなる。
(15) 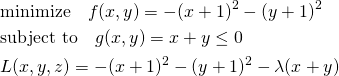
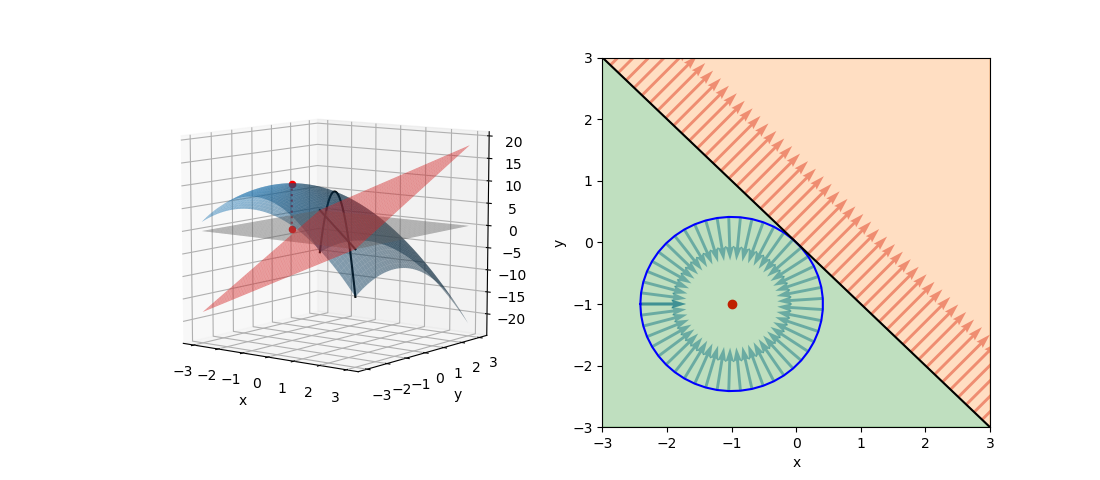
この場合、fの極値は制約条件(緑色)の範囲内にあり、fとgのgradientがgの境界上で逆向きになる。停留点は制約条件内にあることから、λ=0として制約条件の効果をなくし、単純にfの極値問題を解いて以下を得る(∇f =0)。
(16) ![]()
λの符号について
以上の4つのパターンをまとめると、以下のようになる。
| ∇fと∇gが同方向 | ∇fと∇gが逆方向 | |
| fを最小化 | 制約条件内 λ = 0, g(x, y) < 0 |
制約条件外(境界上) λ < 0, g(x, y) = 0 |
| fを最大化 | 制約条件外(境界上) λ > 0, g(x, y) = 0 |
制約条件内 λ = 0, g(x, y) < 0 |
たとえばfを最大化する場合の条件をまとめて書くと、
(17) ![]()
これがKKT条件と呼ばれるもの。
ただし上記の場合分けは、最小化問題か最大化問題かによってλの符号が異なっている。さらに未定乗数を求める関数をここではL = f − λgとしたが、L = f + λgとしている場合もあり、このときはまたλの不等号が逆になってややこしい。
KKT条件では、一般にλ ≥ 0とされるが、元の問題が最小化か最大化か、不等式制約条件を正とするか負とするか、未定乗数法の関数形がf − λgかf + λgか、設定条件によってこの符号が反転する。逆に言えば、もともとのKKT条件がλ ≥ 0と示されているので、最小化(あるいは最大化)に対して−∇gとしたり、L = f ± gを使い分けたり、g ⋚ 0の設定を選んだりしている節がある。
KKT条件
不等式制約条件付きの最適化問題において、Lagrangeの未定乗数法を適用する場合の条件は、一般にKKT条件(Karush-Kuhn-Tucker condition)として示されるが、問題設定の形式を明示する必要がある(あるいは最小化問題と最大化問題でλの不等号を反転させた形で示す)。
最大化問題を基本とし、不等式制約条件は0又は負とする。ラグランジュ関数の制約条件項の符号はマイナスとする。
(18) 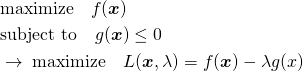
この時、ラグランジュ関数を最大化するKKT条件は
(19) 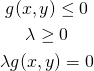
最小化問題の場合には、最大化問題となるように目的関数を反転する。
(20) 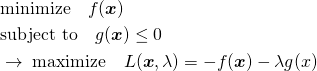
あるいは元のままの関数形として、最小化問題とKKT条件を以下のように設定してもよい。
(21) 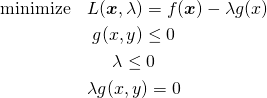
参考サイト
本記事をまとめるにあたって、下記サイトが大変参考になったことに感謝したい。
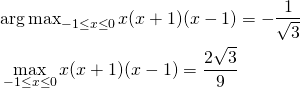
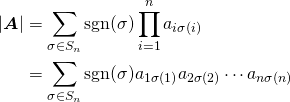
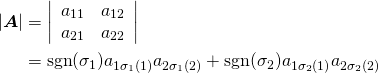
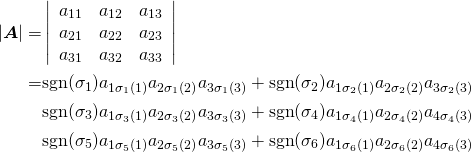
![Rendered by QuickLaTeX.com \begin{equation*} \boldsymbol{x} = \left[ \begin{array}{c} x_1 \\ \vdots \\ x_n \\ \end{array} \right] \end{equation*}](http://taustation.com/wp1/wp-content/ql-cache/quicklatex.com-ca095fba05bd6b51953489329a4dbed5_l3.png)
![Rendered by QuickLaTeX.com \begin{equation*} \boldsymbol{X} = \left[ \begin{array}{ccc} x_{11} & \ldots & x_{1n} \\ \vdots & x_{ij} & \vdots \\ x_{m1} & \ldots & x_{mn} \end{array} \right] \end{equation*}](http://taustation.com/wp1/wp-content/ql-cache/quicklatex.com-b789d485dcbf0314d7147eaf2ac533f1_l3.png)
![Rendered by QuickLaTeX.com \begin{equation*} \boldsymbol{f}(x) = \left[ \begin{array}{c} f_1(x) \\ \vdots \\ f_n(x) \end{array} \right] \end{equation*}](http://taustation.com/wp1/wp-content/ql-cache/quicklatex.com-0c143adda5de76e2ad2d9f369b269daa_l3.png)
![Rendered by QuickLaTeX.com \begin{equation*} \boldsymbol{f}(\boldsymbol{x}) =\ \left[ \begin{array}{c} f_1(x_1, \ldots, x_n) \\ \vdots \\ f_m(x_1, \ldots, x_n) \end{array} \right] \end{equation*}](http://taustation.com/wp1/wp-content/ql-cache/quicklatex.com-e1402f4bca526f4e708673a396a76432_l3.png)
![Rendered by QuickLaTeX.com \begin{equation*} \boldsymbol{F}(x) = \left[ \begin{array}{ccc} F_{11}(x) & \ldots & F_{1n}(x) \\ \vdots & F_{ij} & \vdots \\ F_{m1}(x) & \ldots & F_{mn}(x) \\ \end{array} \right] \end{equation*}](http://taustation.com/wp1/wp-content/ql-cache/quicklatex.com-11b648294a10e1e0bd969847ac5eca32_l3.png)
![Rendered by QuickLaTeX.com \begin{equation*} \frac{d \boldsymbol{f}(x)}{dx} = \left[ \begin{array}{c} \dfrac{d f_1(x)}{dx} \\ \vdots \\ \dfrac{d f_n(x)}{dx} \end{array} \right] \end{equation*}](http://taustation.com/wp1/wp-content/ql-cache/quicklatex.com-2a6538c824acdcefdc708eecff19c4c9_l3.png)
![Rendered by QuickLaTeX.com \begin{equation*} \frac{d \boldsymbol{F}(x)}{dx} = \left[ \begin{array}{ccc} \dfrac{dF_{11}(x)}{dx} & \ldots & \dfrac{dF_{1n}(x)}{dx} \\ \vdots & \dfrac{dF_{ij}(x)}{dx} & \vdots \\ \dfrac{dF_{m1}(x)}{dx} & \ldots & \dfrac{dF_{mn}(x)}{dx} \end{array} \right] \end{equation*}](http://taustation.com/wp1/wp-content/ql-cache/quicklatex.com-fcd4c19cbe8c45de7a76c60b7e7414be_l3.png)
![Rendered by QuickLaTeX.com \begin{equation*} \frac{df(\boldsymbol{x})}{d\boldsymbol{x}} = \left[ \begin{array}{c} \dfrac{\partial f}{\partial x_1} \\ \vdots \\ \dfrac{\partial f}{\partial x_m} \end{array} \right] \end{equation*}](http://taustation.com/wp1/wp-content/ql-cache/quicklatex.com-91df3f7d18edb4fce8d49b885fd8ba4d_l3.png)
![Rendered by QuickLaTeX.com \begin{equation*} \frac{d}{d\boldsymbol{x}}f(\boldsymbol{x}) = \left[ \begin{array}{c} \dfrac{\partial}{\partial x_1} \\ \vdots \\ \dfrac{\partial}{\partial x_m} \end{array}\right] f(\boldsymbol{x}) \end{equation*}](http://taustation.com/wp1/wp-content/ql-cache/quicklatex.com-4f4019636c967a53d820033d665ac0e0_l3.png)
![Rendered by QuickLaTeX.com \begin{equation*} \frac{df(\boldsymbol{X})}{d\boldsymbol{X}} = \left[ \begin{array}{ccc} \dfrac{\partial f}{\partial x_{11}} & \ldots & \dfrac{\partial f}{\partial x_{1n}} \\ \vdots & \dfrac{\partial f}{\partial x_{ij}} & \vdots \\ \dfrac{\partial f}{\partial x_{m1}} & \ldots & \dfrac{\partial f}{\partial x_{mn}} \\ \end{array} \right] \end{equation*}](http://taustation.com/wp1/wp-content/ql-cache/quicklatex.com-420e553422141fba601f4663078d0386_l3.png)
![Rendered by QuickLaTeX.com \begin{equation*} \frac{d}{d\boldsymbol{X}} f(\boldsymbol{X}) = \\ \left[ \begin{array}{ccc} \dfrac{\partial}{\partial x_{11}} & \ldots & \dfrac{\partial}{\partial x_{1n}} \\ \vdots & \dfrac{\partial}{\partial x_{ij}} & \vdots \\ \dfrac{\partial}{\partial x_{m1}} & \ldots & \dfrac{\partial}{\partial x_{mn}} \\ \end{array} \right] f(\boldsymbol{X}) \end{equation*}](http://taustation.com/wp1/wp-content/ql-cache/quicklatex.com-99d9e67383e94425fcf5d01ea0223e26_l3.png)
![Rendered by QuickLaTeX.com \begin{equation*} \frac{d\boldsymbol{f}(\boldsymbol{x})^T}{d\boldsymbol{x}} = \left[ \begin{array}{ccc} \dfrac{\partial f_1}{\partial x_1} & \ldots & \dfrac{\partial f_n}{\partial x_1} \\ \vdots & \dfrac{\partial f_j}{\partial x_i} & \vdots \\ \dfrac{\partial f_1}{\partial x_m} & \ldots & \dfrac{\partial f_n}{\partial x_m} \\ \end{array} \right] \end{equation*}](http://taustation.com/wp1/wp-content/ql-cache/quicklatex.com-311d88dd2427ed7067a39ffafa8dad8d_l3.png)
![Rendered by QuickLaTeX.com \begin{equation*} \frac{d}{d\boldsymbol{x}} \boldsymbol{f}(\boldsymbol{x})^T = \left[ \begin{array}{c} \dfrac{\partial}{\partial x_1} \\ \vdots \\ \dfrac{\parial}{\partial x_m} \end{array} \right] [ f_1(\boldsymbol{x}) \; \ldots \; f_n(\boldsymbol{x}) ] = \left[ \begin{array}{ccc} \dfrac{\partial f_1}{\partial x_1} & \cdots & \dfrac{\partial f_n}{\partial x_1} \\ & \dfrac{\partial f_j}{\partial x_i} &\\ \dfrac{\partial f_1}{\partial x_m} & \cdots & \dfrac{\partial f_n}{\partial x_m} \end{array} \right] \end{equation*}](http://taustation.com/wp1/wp-content/ql-cache/quicklatex.com-9a2aab5d164571bef0094ea7f1eaf975_l3.png)
![Rendered by QuickLaTeX.com \begin{align*} \frac{df}{dx_i} &= \frac{\partial f}{\partial u_1}\frac{\partial u_1}{\partial x_i} + \cdots + \frac{\partial f}{\partial u_j}\frac{\partial u_j}{\partial x_i} + \cdots + \frac{\partial f}{\partial u_n}\frac{\partial u_n}{\partial x_i} \\ \rightarrow \frac{df(\boldsymbol{u}(\boldsymbol{x}))}{d\boldsymbol{x}} &= \left[ \begin{array}{ccc} \dfrac{\partial u_1}{\partial x_1} & \cdots & \dfrac{\partial u_n}{\partial x_1} \\ \vdots && \vdots \\ \dfrac{\partial u_1}{\partial x_m} & \cdots & \dfrac{\partial u_n}{\partial x_m} \\ \end{array} \right] \left[ \begin{array}{c} \dfrac{\partial f}{\partial u_1} \\ \vdots \\ \dfrac{\partial f}{\partial u_n} \end{array} \right] \\ &= \left[ \begin{array}{c} \dfrac{\partial}{\partial x_1} \\ \vdots \\ \dfrac{\partial}{\partial x_m} \end{array} \right] [u_1 \; \cdots \; u_n] \left[ \begin{array}{c} \dfrac{\partial}{\partial u_1} \\ \vdots \\ \dfrac{\partial}{\partial u_n} \end{array} \right] f(\boldsymbol{u}) \end{align*}](http://taustation.com/wp1/wp-content/ql-cache/quicklatex.com-299db8ffb5c52904ccea0f0f44844cb4_l3.png)
![Rendered by QuickLaTeX.com \begin{align*} \frac{d(\boldsymbol{FG})}{dx} &= \frac{d}{dx}\left[\sum_{j=1}^m f_{ij} g_{jk}\right] = \left[\sum_{j=1}^m \left(\frac{df_{ij}}{dx} g_{jk} + f_{ij} \frac{dg_{jk}}{dx} \right)\right] \\ &= \left[ \sum_{j=1}^m \frac{df_{ij}}{dx} g_{jk} \right] + \left[ \sum_{j=1}^m f_{ij} \frac{dg_{jk}}{dx} \right] \end{align*}](http://taustation.com/wp1/wp-content/ql-cache/quicklatex.com-48367a30bf2176691b7825652e570751_l3.png)
![Rendered by QuickLaTeX.com \begin{equation*} \begin{align} & \frac{d}{d\boldsymbol{x}} \left[ \begin{array}{c} a_{11}x_1 + \cdots + a_{1j}x_j + \cdots + a_{1n}x_n \\ \vdots \\ a_{i1}x_1 + \cdots + a_{ij}x_j + \cdots + a_{in}x_n \\ \vdots \\ a_{m1}x_1 + \cdots + a_{mj}x_j + \cdots + a_{mn}x_n \\ \end{array} \right]^T \\ &= \left[ \begin{array}{c} \dfrac{\partial}{\partial x_1} \\ \vdots \\ \dfrac{\partial}{\partial x_j} \\ \vdots \\ \dfrac{\partial}{\partial x_n} \\ \end{array} \right] \left[ \begin{array}{c} a_{11}x_1 + \cdots + a_{1j}x_j + \cdots + a_{1n}x_n \\ \vdots \\ a_{i1}x_1 + \cdots + a_{ij}x_j + \cdots + a_{in}x_n \\ \vdots \\ a_{m1}x_1 + \cdots + a_{mj}x_j + \cdots + a_{mn}x_n \\ \end{array} \right]^T \\ &= \left[ \begin{array}{ccccc} a_{11} & \cdots & a_{i1} & \cdots & a_{m1} \\ \vdots && \vdots && \vdots \\ a_{1j} & \cdots & a_{ij} & \cdots & a_{mj} \\ \vdots && \vdots && \vdots \\ a_{1n} & \cdots & a_{in} & \cdots & a_{mn} \\ \end{array} \right] = \boldsymbol{A}^T \end{align} \end{equation*}](http://taustation.com/wp1/wp-content/ql-cache/quicklatex.com-ae74fc9540924803afe8d58422df0a6f_l3.png)
![Rendered by QuickLaTeX.com \begin{equation*} \left[ \begin{array}{c} \dfrac{\partial}{\partial x_1} \\ \vdots \\ \dfrac{\partial}{\partial x_n} \end{array} \right] [ x_1^2 + \cdots + x_n^2 ] = \left[ \begin{array}{c} 2x_1 \\ \vdots \\ 2x_n \end{array} \right] \end{equation*}](http://taustation.com/wp1/wp-content/ql-cache/quicklatex.com-9a4a53d35d99be2161876f0ebea4b973_l3.png)
![Rendered by QuickLaTeX.com \begin{align*} &\frac{d}{d \boldsymbol{x}} \left( [x_1 \; \cdots \; x_n] \left[ \begin{array}{ccc} a_{11} & \cdots & a_{1n} \\ \vdots & & \vdots \\ a_{n1} & \cdots & a_{nn} \\ \end{array} \right] \left[ \begin{array}{c} x_1 \\ \vdots \\ x_n \end{array} \right] \right)\\ &=\frac{d}{d \boldsymbol{x}} \left( [x_1 \; \cdots \; x_n] \left[ \begin{array}{c} a_{11} x_1 + \cdots + a_{1n} x_n \\ \vdots \\ a_{n1} x_1 + \cdots + a_{nn} x_n \end{array} \right] \right)\\ &= \frac{d}{d \boldsymbol{x}} \left( \left( a_{11} {x_1}^2 + \cdots + a_{1n} x_1 x_n \right) + \cdots + \left( a_{n1} x_n x_1 + \cdots + a_{nn} {x_n}^2 \right) \right) \end{array}\\ &=\left[ \begin{array}{c} \left( 2 a_{11} x_1 + \cdots + a_{1n} x_n \right) + a_{21} x_2 + \cdots + a_{n1} x_n \\ \vdots \\ a_{1n} x_1 + \cdots + a_{1n-1} x_{n-1} + \left( a_{n1} x_1 + \cdots + 2a_{nn} x_n \right) \end{array} \right] \\ &=\left[ \begin{array}{c} \left( a_{11} x_1 + \cdots + a_{1n} x_1 \right) + \left( a_{11} x_1 + \cdots + a_{n1} x_n \right) \\ \vdots \\ \left( a_{n1} x_1 + \cdots + a_{nn} x_n \right) + \left( a_{1n} x_1 + \cdots + a_{nn} x_n \right) \end{array} \right] \end{align*}](http://taustation.com/wp1/wp-content/ql-cache/quicklatex.com-deafe332adeef9ea5b9eb9c5cfbd1ef5_l3.png)
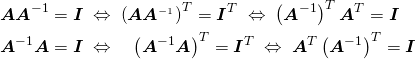
![Rendered by QuickLaTeX.com \begin{align*} \left( [ \boldsymbol{AB} ]_{ij} \right)^T = \left( \sum_k \boldsymbol{A}_{ik} \boldsymbol{B}_{kj} \right)^T = \sum_k \boldsymbol{B}_{jk} \boldsymbol{A}_{ki} =\boldsymbol{B}^T \boldsymbol{A}^T \end{align*}](http://taustation.com/wp1/wp-content/ql-cache/quicklatex.com-e0a675c84ad11bc2c66bd764f6b3dfeb_l3.png)
![Rendered by QuickLaTeX.com \begin{equation*} \left[ \begin{array}{ccc} a_{11} & \cdots & a_{1n} \\ \vdots & & \vdots \\ a_{m1} & \cdots & a_{mn} \\ \end{array} \right] \left[ \begin{array}{c} x_1 \\ \vdots \\ x_n \end{array} \right] = [x_1 \; \cdots \; x_n] \left[ \begin{array}{ccc} a_{11} & \cdots & a_{m1} \\ \vdots & & \vdots \\ a_{1n} & \cdots & a_{mn} \\ \end{array} \right] \end{equation*}](http://taustation.com/wp1/wp-content/ql-cache/quicklatex.com-47268abd1fb09618f4ac57dcd0edb815_l3.png)
![Rendered by QuickLaTeX.com \begin{equation*} [x_1 \; \cdots \; x_n] \left[ \begin{array}{c} x_1 \\ \vdots \\ x_n \end{array} \right] = x_1^2 + \cdots + x_n^2 \end{equation*}](http://taustation.com/wp1/wp-content/ql-cache/quicklatex.com-d7eb4031678ac7ca0faa0eefd7cb4318_l3.png)