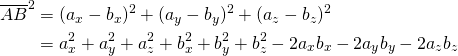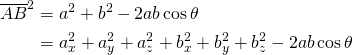カテゴリー: 科学・工学

ポアソン過程～一様分布によるシミュレーション

/ tau / コメントする

概要

一様分布をとる乱数によってランダムな到着をシミュレートし、ポアソン過程の時間間隔や到着回数を理論上の確率分布と比較してみた。

手順

  1. 表計算ソフトで0 ～1の間で平均して10個の発生するように乱数を発生させる
    • 0～1で10個
    • 0～10で100個
    • 0～100で1000個
  2. その値を昇順にソート(到着事象の到着時刻順にあたる)
  3. 到着時刻の分布を確認
  4. 到着時間間隔の分布と指数分布の比較
    1. 各到着時刻間の時間間隔を計算
    2. 時間間隔データの頻度(確率密度に相当)を棒グラフで表示し、指数分布の密度関数のグラフを重ねて比較
    3. 時間間隔データの累積頻度(確率分布に相当)を棒グラフで表示し、指数分布関数のグラフを重ねて表示
  5. 到着回数の分布とPoisson分布の比較

指数分布のデータを得る手順については、 (参考)データ数10個の場合到着時間間隔の計算手順を参照。

Poisson分布のデータを得る手順については、(参考)データ数100個の場合の到着数の計算手順を参照。

以下、データ数10、100、1000の場合の到着時刻の分布、到着間隔の確率密度と確率分布について比較していく。

到着時刻の分布の比較

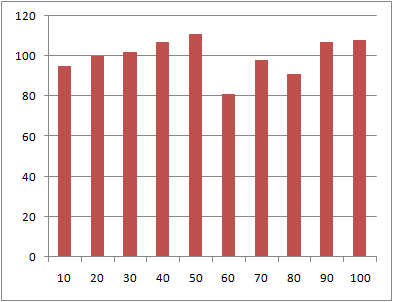
データ数10、100、1000に対する到着時刻の分布を以下に示す。

データ数が多くなるほどグラフは平滑になるが、1000個と比較的多くのデータでもばらつきが見られる。

データ数：10
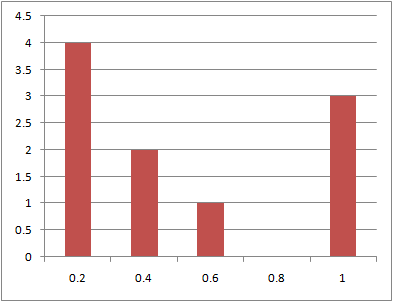
random-arrival-verification-duration0010

データ数：100
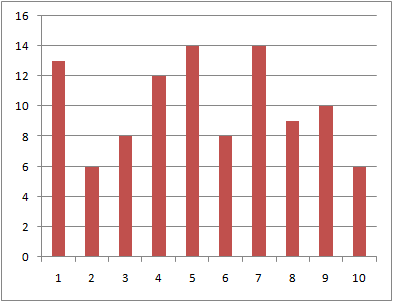
random-arrival-verification-duration0100

データ数：1000
random-arrival-verification-duration1000

到着時間間隔と指数分布の比較

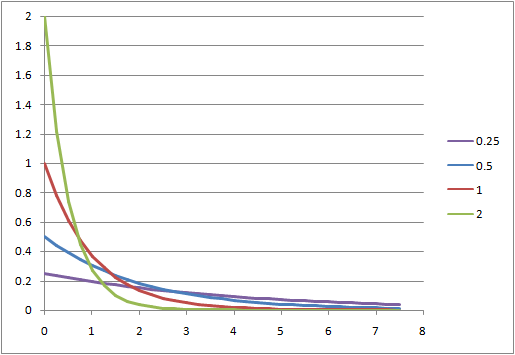
頻度(確率密度)

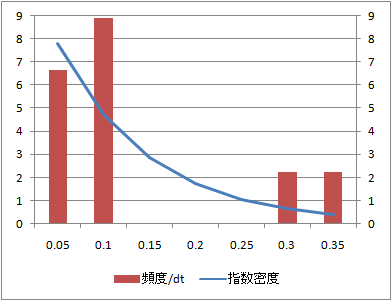
データ数10、100、1000に対する到着時間間隔の頻度分布とこれに相当する指数分布の確率密度関数を比較する。

到着時刻の分布に比べてデータ数100からシミュレーション値と理論値がよく整合している。

データ数：10
random-arrival-verification-exp-density0010

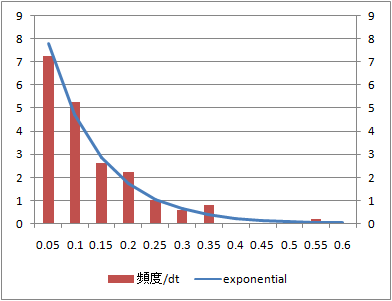
データ数100
random-arrival-verification-exp-density0100

データ数1000
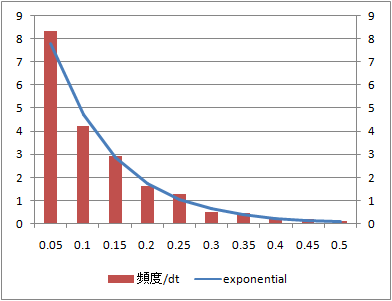
random-arrival-verification-exp-density1000

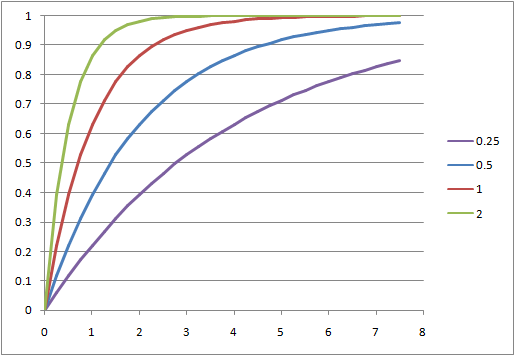
累積頻度(確率分布)

同じデータの累積頻度とこれに相当する指数分布の確率分布関数を比較する。

確率分布に関しては、データ数10と少ないデータでも理論値と類似している。

データ数：10
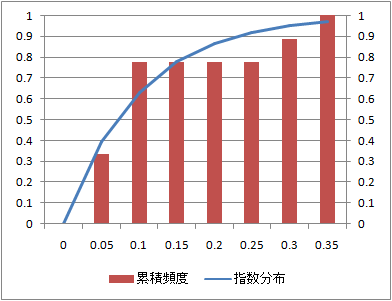
random-arrival-verification-exp-prob0010

データ数：100
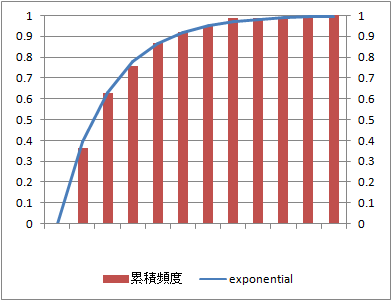
random-arrival-verification-exp-prob0100

データ数：1000
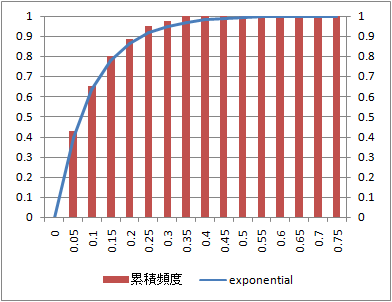
random-arrival-verification-exp-prob1000

到着数の分布とPoisson分布の比較

到着数の分布をみるためには、データ数10個の場合はデータセットにならないため、データ数100、1000で比較してみる。データ数100を10組に、データ数100は100組のデータセットを得ることができる。

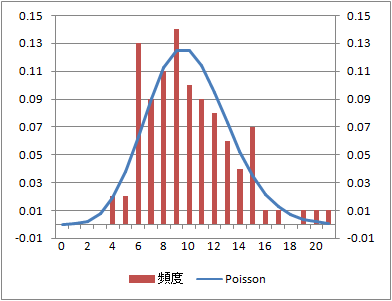
到着数の分布と理論上のPoisson分布との整合性は、データセット数100でもそれほどよくない。

データ数：100(データセット数：10)
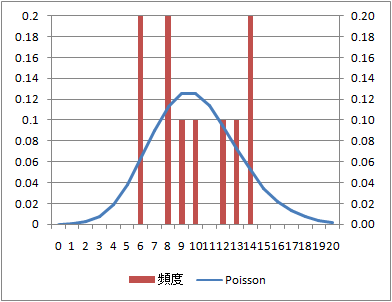
random-arrival-verification-poisson-prob0100

データ数：1000(データセット数100)
random-arrival-verification-poisson-prob1000

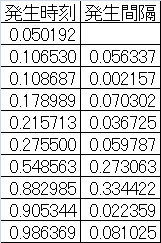
(参考)データ数10個の場合到着時間間隔の計算手順

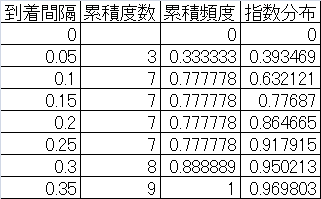
以下の表は、0～1の範囲で10個の乱数を発生させ、それらを昇順にソートして発生間隔を計算したもの。

statistics-random-arrival-verification-1

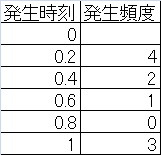
まず、これらの発生時刻を、一定の階級幅で度数分布に分ける。データ数が10個の場合はばらつきが大きいが、データ数が多くなると、これが一様分布に近づくと期待される。

statistics-random-arrival-verification-2

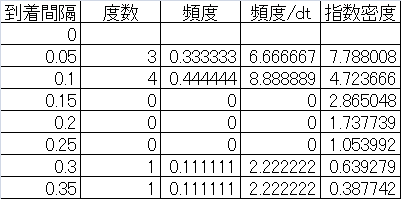
次に、到着時間間隔の度数分布とその頻度を計算する。これを指数分布の密度関数と比較するため、時間間隔dtで除している。一番右の欄は、到着率10の指数分布の密度関数の値。

statistics-random-arrival-verification-3

最後に、指数分布の確率関数と比較をするため、到着間隔の累積度数と頻度を計算する。一番右の欄は、到着率10の確率分布関数の値。

statistics-random-arrival-verification-4

(参考)データ数100個の場合の到着数の計算手順

元データは、到着時刻を昇順にソートしたもの。

 random-arrival-verification-poisson1

これらのデータの、0以上1未満、1以上2未満、・・・・、9以上10未満の10組ごとのデータ数を数える。

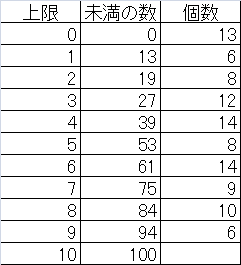
random-arrival-verification-poisson2

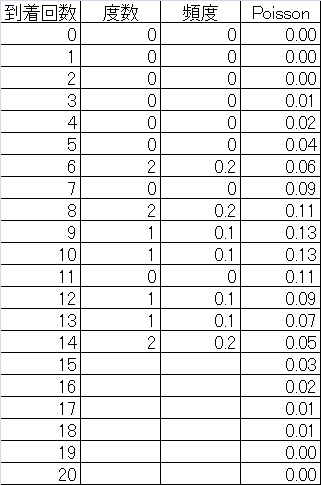
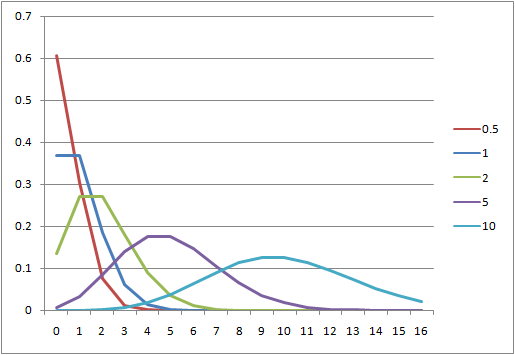
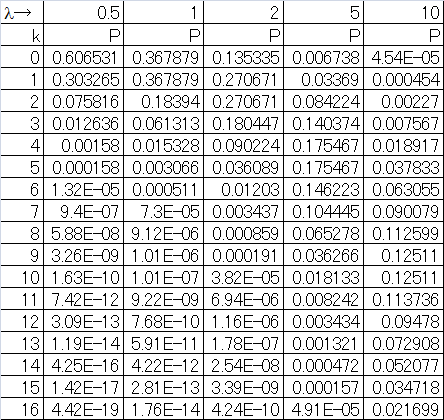
これらについて、到着回数ごとの頻度分布に整理する。下表一番右の欄は、到着率10に対するPoisson確率値。

random-arrival-verification-poisson3

 

ポアソン過程の到着数～ポアソン分布

/ tau / コメントする

単位時間当たりの到着率\lambdaのポアソン過程において、t時間の間にk回の到着が発生する確率を考える。

tをn等分し、\Delta t = t / nとする。この間にk回の到着が発生し、(n - k)回は到着が発生しないとすると、その確率は次の二項分布で表される。

(1)   \begin{equation*} P(k;t;n) = {}_n C_k (\lambda \Delta t)^k (1 - \lambda \Delta t)^{n-k} \end{equation*}

この式を、以下のように展開しておく。

(2)   \begin{eqnarray*} P(k;t;n) &=& \frac{n!}{k! (n-k)!} (\lambda \Delta t)^k (1 - \lambda \Delta t)^{n - k} \\ &=& \frac{n(n - 1) \cdots (n - k + 1)}{k!} \left( \frac{\lambda t}{n} \right)^k \left(1 - \frac{\lambda t}{n} \right)^{n - k} \end{eqnarray*}

ここでn \to \infty (\Delta t \rightarrow 0)の極限を考える。まず前2項については、

(3)   \begin{eqnarray*} &&\lim_{n \to \infty} \frac{n(n - 1) \cdots (n - k + 1)}{k!} \left( \frac{\lambda t}{n} \right)^k \\ &=& \lim_{n \to \infty} \frac{1 \cdot \left(1 - \cfrac{1}{n} \right) \cdots \left(1 - \cfrac{k - 1}{n} \right)}{k!} (\lambda t)^k \\ &=& \frac{(\lambda t)^k}{k!} \end{eqnarray*}

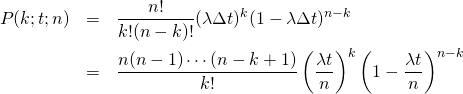
また3項目については-n / \lambda t = r \to \inftyとおいて、

(4)   \begin{equation*} \lim_{r \to \infty} \left( 1 + \frac{1}{r} \right)^{- r \lambda t - k} = \lim_{r \to \infty}\left[ \left(1 + \frac{1}{r} \right)^{- r \lambda t} \left( 1 + \frac{1}{r} \right)^{-k} \right] = e^{- \lambda t} \end{equation*}

通常、Poisson分布の表現は上式において\lambda t \to \lambdaとして表現されるが、この場合の\lambdaは観測時間内の平均到着数として考える。ここでは、単位時間あたりの到着率\lambdaと観測時間tを明確にするため\lambda tと表現した。

以上から、到着率\lambdaのポアソン過程において、観測時間tの間にk回の到着が発生する確率は以下のPoisson分布で与えられる。

(5)   \begin{equation*} P(k; t; \lambda) = \frac{(\lambda t)^k}{k!} e^{- \lambda t} \end{equation*}

 

 

ポアソン過程の到着間隔～指数分布

/ tau / コメントする

離散的な方法による確認

単位時間あたりの到着率\lambdaのポアソン過程において、時刻0に到着が発生した後、次の到着があるまでの時間間隔がt以下である確率を考える。

tをn等分し、\Delta t = t / nとすると、到着間隔がt以下なので、連続して到着しなかった後に到着が発生する事象を重ね合わせて、以下のように表せる。

(1)   \begin{eqnarray*} P(\tau \le t) &=& \lambda \Delta t + (1 - \lambda \Delta t)\lambda \Delta t + \cdots + (1 - \lambda \Delta t)^{n-1} \lambda \Delta t \\ &=& \lambda \Delta t \frac{1 - (1 - \lambda \Delta t)^n}{1 - (1 - \lambda \Delta t)} \\ &=& 1 - \left( 1 - \frac{\lambda t}{n} \right) \end{eqnarray*}

ここで-n/\lambda t = rとおいてr \to \inftyの極限をとると、

(2)   \begin{equation*} \lim_{r \to \infty} 1 - \left( 1 + \frac{1}{r} \right)^{-r \lambda t} = 1 - e^{- \lambda t} \end{equation*}

となって指数分布の確率分布関数を得る。

確率密度関数を直接求める方法

到着時間間隔の確率密度関数をf(x)とし、0 \sim tの間は到着が発生せず、t \sim t + \Delta tで到着が発生する場合を考える。

(3)   \begin{equation*} f(t) \Delta t = \left( 1 - \int_0^t f(t) dt \right) \lambda \Delta t \end{equation*}

これより、

(4)   \begin{equation*} f(t) = \lambda - \lambda \int_0^t f(t) dt \end{equation*}

両辺をtで微分して、

(5)   \begin{equation*} f'(t) = - \lambda f(t) \end{equation*}

この微分方程式の解は、

(6)   \begin{equation*} f(t) = C e^{- \lambda t} \end{equation*}

確率密度関数なので、全定義域の積分値が1となることから、

(7)   \begin{equation*} \int_0^\infty C e^{- \lambda t} dt = \left[ - \frac{C}{\lambda} e^{- \lambda t} \right]_0^\infty = 1 \end{equation*}

これよりC = \lambdaを得るので、確率密度関数は以下のように得られる。

(8)   \begin{equation*} f(t) = \lambda e^{- \lambda t} \end{equation*}

Poisson分布から導く方法

ポアソン過程に関して、以下のPoisson分布を考える。

(9)   \begin{equation*} P(X = k) = \frac{(\lambda t)^k}{k!} e^{- \lambda t} \end{equation*}

ここで、時刻T = 0 \sim tの間に全く到着がない確率はその時間の間k = 0であるから、

(10)   \begin{equation*} F(T > t) = e^{- \lambda t} \end{equation*}

ここで、到着時間間隔がt以下である確率は、T = 0 \sim tの間に1回以上到着がある事象の和であり、「1回も到着がない」事象の余事象でもある。これより、以下の指数分布の分布関数を得る。

(11)   \begin{equation*} F(T \le t) = 1 - e^{- \lambda t} \end{equation*}

 

ポアソン分布

/ tau / コメントする

Poisson分布の標準形

ポアソン過程の到着数に現れる、離散確率分布。

(1)   \begin{equation*} P(k; \lambda) = \frac{\lambda ^ k}{k!} e^{- \lambda} \end{equation*}

全事象の確率が1となることの確認

(2)   \begin{equation*} \sum_{k=0}^{\infty} \frac{\lambda ^ k}{k!} e^{- \lambda} = e^{\lambda} e^{-\lambda} = 1 \end{equation*}

平均

(3)   \begin{eqnarray*} E(k) &=& \sum_{k=0}^{\infty} k \frac{\lambda ^ k}{k!} e^{- \lambda} = e^{-\lambda} \sum_{k=1}^{\infty} \frac{\lambda ^ k}{(k - 1)!} = e^{-\lambda} \sum_{k=0}^{\infty} \frac{\lambda ^ {k + 1}}{k!} = e^{-\lambda} \lambda \sum_{k=0}^{\infty} \frac{\lambda ^ {k}}{k!} \\ &=& \lambda e^{-\lambda} e^{\lambda} \\ &=& \lambda \end{eqnarray*}

この過程で以下のようになっていることに留意。

(4)   \begin{eqnarray*} \sum_{k=0}^{\infty} k \frac{\lambda ^ k}{k!} &=& 0\cdot \frac{\lambda ^0}{0!} + 1 \cdot \frac{\lambda ^1}{1!} + 2 \cdot \frac{\lambda ^2}{1 \cdot 2} + 3 \cdot \frac{\lambda ^3}{1 \cdot 2 \cdot 3} + \cdots + k\frac{\lambda ^k}{1 \cdots k} + \cdots \\ &=& \frac{\lambda ^1}{1} + \frac{\lambda ^2}{1} + \frac{\lambda ^3}{1 \cdot 2} + \cdots + \frac{\lambda ^k}{1 \cdots (k-1)} + \cdots \left( = \sum_{k=1}^{\infty} \frac{\lambda ^ k}{(k - 1)!} \right) \\ &=& \frac{\lambda ^1}{0!} + \frac{\lambda ^2}{1!} + \frac{\lambda ^3}{2!} + \cdots + \frac{\lambda ^{k}}{k-1} + \cdots \left( = \sum_{k=0}^{\infty} \frac{\lambda ^ {k + 1}}{k!} \right) \\ &=& \lambda \sum_{k=0}^{\infty} \frac{\lambda ^k}{k!} \end{eqnarray*}

分散

(5)   \begin{equation*} V(k) &=& \sum_{k=0}^{\infty} k^2 \frac{\lambda ^k}{k!} e^{- \lambda} - \lambda^2 = e^{- \lambda} \sum_{k=0}^{\infty} k^2 \frac{\lambda ^k}{k!} - {\lambda}^2 \end{equation*}

第一項の和の部分については、

(6)   \begin{eqnarray*} \sum_{k=0}^{\infty} k^2 \frac{\lambda ^k}{k!} &=& \sum_{k=1}^{\infty} k \frac{\lambda ^k}{(k - 1)!} = \sum_{k=0}^{\infty} (k + 1) \frac{\lambda ^(k + 1)}{k!} \\ &=& \lambda \sum_{k=0}^{\infty} k \frac{\lambda ^k}{k!} + \lambda \sum_{k=0}^{\infty} \frac{\lambda ^k}{k!} \\ &=& \lambda ^2 e^\lambda + \lambda e^\lambda \end{eqnarray*}

したがって分散は以下のように得られる。

(7)   \begin{equation*} V(k) = \lambda \end{equation*}

確率分布の形状と考察

Poisson分布の形状の特徴は以下の通り。

  • \lambda < 1のときは単調減少
  • \lambda = 1のときk = 0, 1に対する確率が等しく、約0.368
  • \lambda > 1でピークが現れる。

statistics-poisson-distribution

statistics-poisson-table

\lambda < 1は、その観測期間内に平均して1回も来ないようなケース。たとえば\lambda = 0.5だと、平均して20分に1度来訪者が来ているとき次の10分に何人来そうか？といったイメージで、全く来ない確率が約60%、1人来る確率が約30%、2人以上来る確率が1割程度となる。ランダム事象と仮定したときの、災害に当てはめても興味深い。

\lambda = 1は、単位時間あたりの到着率に観測時間を乗じた値が1ということであり、平均的にその観測時間内に1回到着しそうな状況にあたる。このような状況でも全く到着がない確率と1回到着する確率が等しく約37%、2回以上到着する確率が25%強となる。

\lambda > 1の場合、\lambdaの値に近いところで確率が最大となり、\lambdaの値が大きくなるにしたがって高さは低く、裾野が広くなり対称形に近くなる。

 

指数分布

/ tau / コメントする

標準形

ポアソン過程の到着時間間隔や信頼性の故障発生間隔に現れる連続確率分布。単位時間当たりの到着率や発生率を\lambdaとしたとき、時刻tを確率変数とした確率密度関数と確率分布関数は以下の形になる。

(1)   \begin{equation*} f(t) = \lambda e^{- \lambda t} \end{equation*}

(2)   \begin{equation*} F(t) = 1 - e^{- \lambda t} \end{equation*}

全事象の確率が1となることの確認

(3)   \begin{equation*} \int_0^\infty \lambda e^{- \lambda t} dt = \left[ e^{-\lambda t} \right]_0^\infty = 1 \end{equation*}

平均

(4)   \begin{eqnarray*} E(t) &=& \int_0^\infty t \lambda e^{- \lambda t} dt = \int_0^\infty x e^{-x} d \frac{x}{\lambda} \\ &=& \frac{1}{\lambda} \left( \int_0^\infty e^{-x} dx - \left[ x e^{-x} \right]_0^\infty \right) = \frac{1}{\lambda} \left[ - e^{-x} - x e^{-x} \right]_0^\infty \\ &=& \frac{1}{\lambda} \end{eqnarray*}

分散

(5)   \begin{eqnarray*} V(t) &=& \int_0^\infty t^2 \lambda e^{-\lambda t} dt - \left( \frac{1}{\lambda} \right)^2 = \frac{1}{\lambda^2} \int_0^\infty x^2 e^{-x} dx - \frac{1}{\lambda^2} \\ &=& \frac{1}{\lambda^2} \left( 2 \int_0^\infty x e^{-x} dx - \left[ x^2 e^{-x} \right]_0^\infty - 1 \right) \\ &=& \frac{1}{\lambda^2} \left( \left[ -2 e^{-x} -2x e^{-x} - x^2 e^{-x} \right]_0^\infty - 1 \right) \\ &=& \frac{1}{\lambda^2} \end{eqnarray*}

確率密度と確率分布の形状

確率密度は当然、指数関数の形状となるため、t = 0で最大値をとる単調減少関数。

このため、到着時間間隔がt以下となるような確率は、t = 0での増加率が最も大きく、その後水平に近くなっていく。

statistics-exponential-density

statistics-exponential-distribution

指数分布に関する考察

指数分布はランダムに到着する客の到着時間間隔やトランザクションの時間、信頼性における機器の故障などに現れるが、「平均発生時間間隔」があるのに何故確率密度がそれを中心とした凸型にならずに単調現象なのか、なかなかストンと胸に落ちなかった。

いろいろ考えていて、「無記憶性」の発生事象ということを考えると、次のように整理はできる。

  • 前の事象の発生と次の事象の発生に、何の因果関係もない
  • 次の瞬間、瞬間に事象が起こる率は一定
  • ということは、前の事象が起こってすぐに次の事象が起こる率\lambda \Delta tより、一定時間後に（それまで発生せず)事象が発生する確率の方が小さくなる(1 - \lambda \Delta t)^{n-1} \lambda \Delta t
  • ゆえに、確率密度は単調現象

 

 

 

ネイピア数

/ tau / コメントする

概要

ネイピア数(Napier’s constant)は自然対数の底で、一般に記号eで表される。オイラー数(Euler’s number)と呼ばれることもある。

(1)   \begin{equation*} e = 2.7182818284590452353602874 \cdots \end{equation*}

定義

ヤコブ・ベルヌーイによる定義。

(2)   \begin{equation*} e = \lim_{n \to \infty} \left( 1 + \frac{1}{n} \right) ^n \end{equation*}

性質

(3)   \begin{equation*} \frac{d}{dx} e^x = e_x \end{equation*}

(4)   \begin{equation*} \int e^x = e_x + {\rm const} \end{equation*}

(5)   \begin{equation*} \frac{d}{dx} \ln x = \frac{1}{x} \end{equation*}

(6)   \begin{equation*} \int \frac{dx}{x} = \ln x + {\rm const} \end{equation*}

テイラー展開

(7)   \begin{eqnarray*} e^x &=& \sum_{n=0}^{\infty} \frac{x^n}{n!} \\ &=& 1 + \frac{x}{1!} + \frac{x^2}{2!}+ \frac{x^3}{3!} \cdots \end{eqnarray*}

 

三角関数 – 加法定理

/ tau / コメントする

加法定理の一覧

(1)   \begin{eqnarray*} \sin ( \alpha \pm \beta) &=& \sin \alpha \cos \beta \pm \cos \alpha \sin \beta \\ \cos ( \alpha \pm \beta ) &=& \cos \alpha \cos \beta \mp \sin \alpha \sin \beta \end{eqnarray*}

導出

第1ステップ – 等式の一つを導出

まず、以下のような図を考える。

math_trigonometry_additiontheorem_1

ABの長さを余弦定理で表す。

(2)   \begin{equation*} ( \cos \alpha - \cos \beta )^2 + ( \sin \alpha - \sin \beta )^2 = 1^2 + 1^2 - 2 \cos (\alpha - \beta) \end{equation*}

これより以下を得るが、これは加法定理のうちの一つに対応している。

(3)   \begin{equation*} \cos (\alpha - \beta) = \cos \alpha \cos \beta + \sin \alpha \sin \beta \end{equation*}

なお上式は、cosの性質からαとβの大小関係に関わらず成り立つ。

第2ステップ – 符号の反転

式(3)でβ → – βと置くと以下を得る。

(4)   \begin{equation*} \cos (\alpha + \beta) = \cos \alpha \cos \beta - \sin \alpha \sin \beta \end{equation*}

第3、4ステップ – cosからsinへの変換と符号の反転

式(3)でα → α+π/2と置くと以下を得る。

(5)   \begin{eqnarray*} \cos \left( \alpha + \frac{\pi}{2} - \beta \right) &=& \cos \left( \alpha + \frac{\pi}{2} \right) \cos \beta - \sin \left( \alpha + \frac{\pi}{2} \right) \sin \beta \\ - \sin ( \alpha - \beta ) &=& - \sin \alpha \cos \beta + \cos \alpha \sin \beta \\ \sin ( \alpha - \beta ) &=& \sin \alpha \cos \beta - \cos \alpha \sin \beta \end{eqnarray*}

また上式においてβ → – βと置くと以下を得る。

(6)   \begin{eqnarray*} \sin ( \alpha + \beta ) &=& \sin \alpha \cos \beta + \cos \alpha \sin \beta \end{eqnarray*}

これで加法定理に関する4つの式が得られた。

一般角への拡張

αやβが第3象限、第4象限にあるときは、それらからπ/2、πを減じて冒頭の図に対応させ、式変形をすることで同じ解を得る。

例えば下図のように、αが第3象限、βが第1象限にあるケースを考える。

math_trigonometry_additiontheorem_2

ここでα = α’ + π/2と置けば、α’について加法定理が成り立つことが分かっているので、

(7)   \begin{eqnarray*} \sin ( \alpha ' \pm \beta) &=& \sin \alpha ' \cos \beta \pm \cos \alpha ' \sin \beta \\ \cos ( \alpha ' \pm \beta ) &=& \cos \alpha ' \cos \beta \mp \sin \alpha ' \sin \beta \end{eqnarray*}

αとα’の関係より、

(8)   \begin{eqnarray*} \sin \left( \alpha - \frac{\pi}{2} \pm \beta \right) &=& \sin \left( \alpha - \frac{\pi}{2} \right) \cos \beta \pm \cos \left( \alpha - \frac{\pi}{2} \right) \sin \beta \\ \cos \left( \alpha - \frac{\pi}{2} \pm \beta \right) &=& \cos \left( \alpha - \frac{\pi}{2} \right) \cos \beta \mp \sin \left( \alpha - \frac{\pi}{2} \right) \sin \beta \end{eqnarray*}

これらより、以下の下方定理がこのケースについて成り立つことが示される。

(9)   \begin{eqnarray*} - \cos ( \alpha \pm \beta) &=& - \cos \alpha \cos \beta \pm \sin \alpha \sin \beta \\ \sin ( \alpha \pm \beta ) &=& \sin \alpha \cos \beta \pm \cos \alpha \sin \beta \end{eqnarray*}

 

直線のパラメータ表示と操作

/ tau / コメントする

直線のパラメータ表示

たとえば2次元の直線のパラメータ表示は、以下のように一つのパラメータtに対してxとyが計算される方法。

    $$ \left\{ \begin{align*} x = a t + b \\ y = c t + d \end{align} \right. $$

直線の決定

通過点と方向が与えられた場合

直線が通過すべき点(px, py)と、直線の方向(vx, vy)が与えられた場合のパラメータ表示を決定する。

通過点でパラメータがt = 0とすればpxとpyが定まり、tが1単位増えた時のxとyの増分が直線の方向に対応することから、以下のように表される。

    $$ \left\{ \begin{align*} x = v_x t + p_x \\ y = v_y t + p_y \end{align} \right. $$

なおこれらを、パラメータtに対応した直線状の点の位置ベクトル{\bf x}、通過点の位置ベクトル{\bf p}、方向ベクトル{\bf v}で表示すると下記のようになる。

    \[{\bf x} = {\bf v} t + {\bf p}\]

2つの通過点が与えられた場合

2つの点p(px, py)とq(qx, qy)が与えられた場合の直線のパラメータ表示を決定する。

点pでt = 0、点qでt = 1とすれば、以下の式が得られる。

    $$ \left\{ \begin{align*} x = (q_x - p_x) t + p_x \\ y = (q_y - p_y) t + p_y \end{align} \right. $$

これをベクトル表示すれば以下の通り。

    \[{\bf x} = ( {\bf q} - {\bf p} ) t + {\bf p}\]

直線の式との関係

一般に直線の式は以下で与えられる。

    \[ax + by + c = 0\]

一方で媒介変数された直線の式からパラメーターを消去すると以下のようになる。

    \[\frac{x - p_x}{v_x} = \frac{y - p_y}{v_y}\]

これを変形すると、先の直線の式との対応関係がわかる。

    \[v_y x - v_x y -v_x p_x + v_y p_y = 0\]

交点の特定

以下の2つの直線の交点を求める。

    $$ \left\{ \begin{align*} {\bf x}_1 = {\bf v}_1 t_1 + {\bf p}_1 \\ {\bf x}_2 = {\bf v}_2 t_2 + {\bf p}_2 \end{align} $$

これを要素表示に展開する。

    $$ \left\{ \begin{align*} x_1 = v_{1x} t_1 + p_{1x} \\ y_1 = v_{1y} t_1 + p_{1y} \\ x_2 = v_{2x} t_2 + p_{2x} \\ y_2 = v_{2y} t_2 + p_{2y} \end{align} $$

ここでx1 = x2、y1 = y2と置いて、t1、t2を未知数とした以下の方程式を得る。

    $$ \left\{ \begin{align*} v_{1x} t_1 + p_{1x} = v_{2x} t_2 + p_{2x} \\ v_{1y} t_1 + p_{1y} = v_{2y} t_2 + p_{2y} \end{align} $$

この方程式を行列で表示すると以下の通り。

    \[\left[ \begin{array}{cc} v_{1x} & -v_{2x} \\ v_{1y} & -v_{2y} \end{array} \right] \left[ \begin{array}{c} t_1 \\ t_2 \end{array} \right] = \left[ \begin{array}{c} p_{2x} - p_{1x} \\ p_{2y} - p_{1y} \end{array} \right] = \left[ \begin{array}{c} \Delta p_x \\ \Delta p_y \end{array} \right]\]

これを解いて以下を得る。

    $$ \left\{ \begin{align*} t_1 = \frac{-v_{2y} \Delta p_x + v_{2x} \Delta p_y}{-v_{1x}v_{2y} + v_{1y} v_{2x}} \\ t_2 = \frac{-v_{1y} \Delta p_x + v_{1x} \Delta p_y}{-v_{1x}v_{2y} + v_{1y} v_{2x}} \end{align} \right. $$

これらの式は分母がゼロのときは解をもたないが、これは{\bf v}_1と{\bf v}_2を90度回転させたベクトルが直角であること、すなわち2つの直線の方向が平行であることを示している。

さらに2つの直線がまったく一致するときは、分母・分子ともゼロとなり、解は不定となる。

ここで、交点の座標を確認する。

    $$ \begin{align*} x &= v_{1x} t_1 + p_{1x} = v_{2x} t_2 + p_{2x} \\ &= \frac{v_{1y} v_{2x} p_{1x} - v_{1x} v_{2y} p_{2x} + v_{1x} v_{2x}(p_{2y} - p_{1y})} {-v_{1x} v_{2y} + v_{1y} v_{2x}} \\ y &= v_{1y} t_1 + p_{1y} = v_{2y} t_2 + p_{2y} \\ &= \frac{v_{1y} v_{2y} (p_{2x} - p_{1x}) - v_{1x} v_{2y} p_{1y} + v_{1y} v_{2x} p_{2y}} {-v_{1x} v_{2y} + v_{1y} v_{2x}} \end{align} $$

当然この結果は、パラメータ表示の2直線からパラメータt1、t2を消去して陰関数表示をした以下の方程式の解と一致する。

    $$ \left\{ \begin{align*} v_{1y} x - v_{1x} y = v_{1y} p_{1x} - v_{1x} p_{1y} \\ v_{2y} x - v_{2x} y = v_{2y} p_{2x} - v_{2x} p_{2y} \end{align} \right. $$

 

交点の位置

パラメータ表示の場合、基準点においてt = 0とし、方向ベクトルの先、あるいはそれに相当する2つ目の点においてt = 1などとすれば、基準点から方向ベクトルの先のtは正の値、逆方向ではtが負の値になる。

これを利用して、二つの直線の交点が基準点より前方／後方どちらの側にあるか、あるいは半直線に交点が存在するか、といった判定が容易に可能となる。

math_geom_line1

 

ベクトルの内積

/ tau / コメントする

ベクトルの内積の表現には、要素表示を用いたものと幾何的なものの2つがある。

    $$ {\bf a} \cdot {\bf b} = a_x b_x + a_y b_y + a_z b_z = | {\bf a} | | {\bf b} | \cos \theta $$

2つの表現が等価であることを証明するのに、下図のように2つのベクトルで張られた三角形の\oberline{AB}の長さを考える。

math_vector_innerprod_1

まずベクトルの成分で計算した場合は、

    $$ \begin{align*} \overline{AB}^2 &= (a_x - b_x)^2 + (a_y - b_y)^2 + (a_z - b_z)^2 \\ &= a_x^2 + a_y^2 + a_z^2 + b_x^2 + b_y^2 + b_z^2 - 2 a_x b_x - 2 a_y b_y - 2 a_z b_z \end{align} $$

また余弦定理を用いて計算した場合は、a = | {\bf a} | , \: b = | {\bf b} |として以下のようになる。

    $$ \begin{align*} \overline{AB}^2 &= a^2 + b^2 - 2ab \cos \theta \\ &= a_x^2 + a_y^2 + a_z^2 + b_x^2 + b_y^2 + b_z^2 - 2ab \cos \theta \end{align} $$

上記2つが等しいことから、以下が得られる。

    $$ a_x b_x + a_y b_y + a_z b_z = ab \cos \theta $$

2次元の場合は、z成分を0とおいてx成分とy成分のみについて考えればよい。