基本
条件付き確率~ベイズの定理(Baye’s theorem)はとっつきにくいが、記号の使い方や図で理解することでわかりやすくなる。
事象![]() が起こったときの事象
が起こったときの事象![]() の条件付き確率は、以下で計算される。
の条件付き確率は、以下で計算される。
(1) ![]()
事象の記号にに![]() や
や![]() を使うのが一般的だが、私にはどちらが条件で、どちらを最終的に求めたいのかわかりにくいので、ここで
を使うのが一般的だが、私にはどちらが条件で、どちらを最終的に求めたいのかわかりにくいので、ここで![]() :Target、
:Target、![]() :Conditionの記号を使った
:Conditionの記号を使った
![]() は事前確率、
は事前確率、![]() は事後確率、
は事後確率、![]() は同時確率と呼ばれる。
は同時確率と呼ばれる。
ここで![]() から、以下のようにも表現される。
から、以下のようにも表現される。
(2) ![]()
一般表現
より一般的には、事象![]() は互いに排反で、
は互いに排反で、![]() とするとき、
とするとき、
(3) 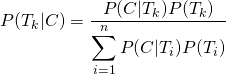
たとえば![]() が背反する2事象、すなわち
が背反する2事象、すなわち![]() の場合は以下のようになる。
の場合は以下のようになる。
(4) ![]()
具体例として、癌などの難病の検査に関する問題が見られる。
また、ベイズの定理についてこちらでもう少し詳しい解釈をしている。