概要
条件付き確率の代表的な問題として、2人の子の性別問題をよく見かけるが、前提条件によって答えが異なることを明確にしている例は少ない。
また、この問題がベン図を用いた分析や、ベイズの定理の親和性についても考えてみる。
兄妹の場合
まず準備として、以下の問題を考える。
普通に考えれば、男か女どちらかなのだから、確率は1/2と考えるが、まずは生真面目にすべての事象を並べてみる。
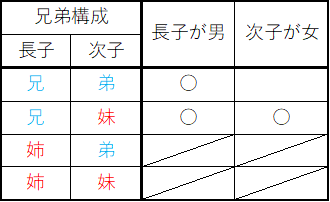
上の子が兄か姉かに関係なく下の子が女である確率は1/2と直感的に考えられるが、それが確認できた。
一応、以下の様なベン図を考えてみる。図中、色付けしたところが条件下での事象で、濃い色が事後確率として求めたい部分。
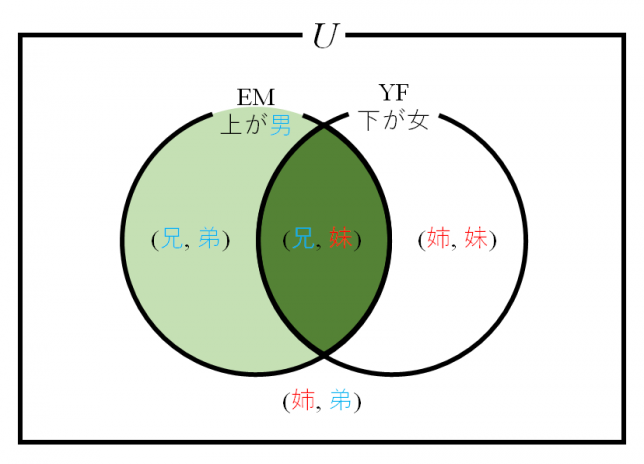
ここで記号E/Yはelder/younger、M/Fはmail/femailを表す。この場合、上の子が男(事象EM)のもとでの下の子が女(事象EMかつYF)ということになり、EMの要素が(男, 男)、(男, 女)の2つに対してEMかつYFの要素は(男,女)だけなので、確率は1/2となる。
なお、ベン図の代わりに場合分けの表で整理してみると、以下の様になる。
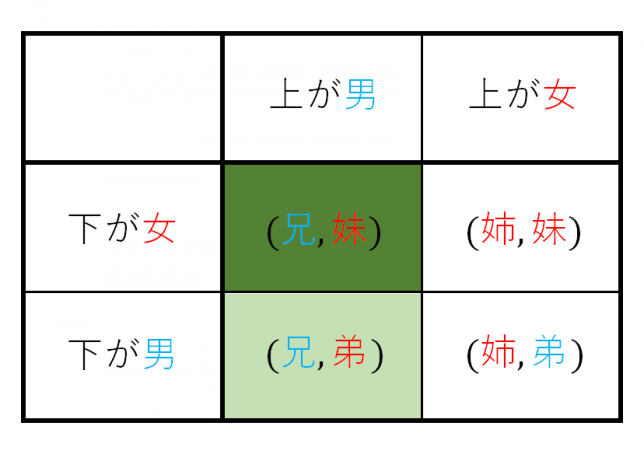
これを敢えてベイズの定理で書くと以下の様になるが、まあ当たり前という感じ。
(1) ![]()
これをベイズの定理の別の表現で書くと以下の様になる。
(2) 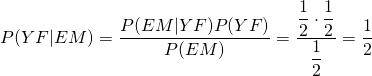
ただし![]() としているが、この項の考え方は結局求めたい確率と同じ道筋で考えなければならない。
としているが、この項の考え方は結局求めたい確率と同じ道筋で考えなければならない。
いずれにしてもこの問題は、第一子が男であろうが女であろうが、第二子が男か女かと問われれば、確率1/2でどちらか、という自然な結果となり、ベン図や場合分け表、ベイズの定理を使ったとしても、あまり恩恵は得られない。
区別なしの場合
次に以下の様な問題を考える。
これも普通に考えれば、男か女どちらかなのだから、確率は1/2と考えてしまいそうになるが、まじめに事象を考えてみる。
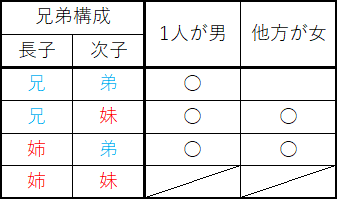
この場合は1人が男とわかっているので、(姉, 妹)の事象は存在しなくなり、もう1人が女というだけで姉か妹かの区別はないことから、確率は2/3となる。
これをベン図で描いてみると以下のようになるが、男と女の組み合わせが2通りあることを確認する点では、上のような整理のほうがわかりやすい。
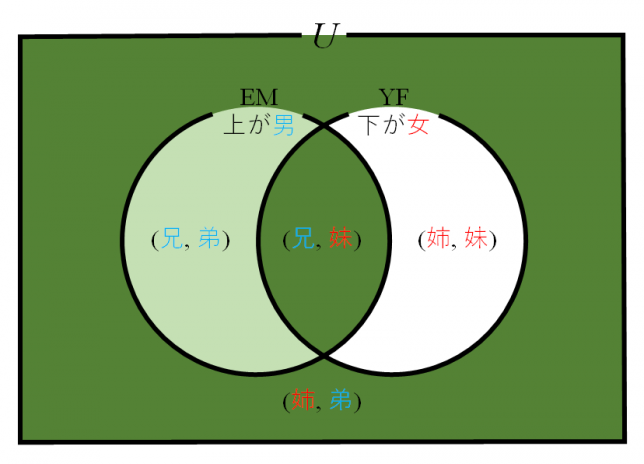
場合分けの表は以下の通りになる。
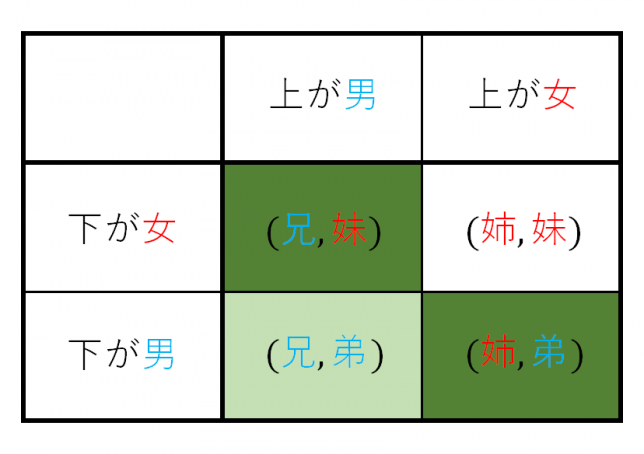
これをベイズの定理で表現すると以下のようになる。
(3) 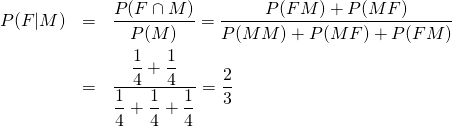
条件付き確率から求める方法は、式(2)と同じ理由でメリットがない。
順番がある場合
次に以下の様な問題を考える。
この場合は上の子と下の子を区別していないので、一つ前の問題と同じ答えになりそうだが、事象を列挙してみる。
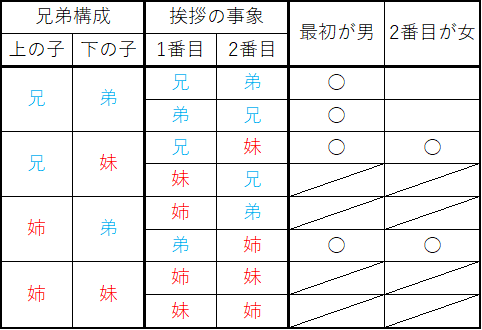
この問題でも、2人とも女のケースが除かれるが、兄弟構成に対して挨拶の順番がそれぞれ2通りずつあり、2人とも男の場合は兄、弟のいずれも最初に挨拶しうるので前提条件の事象に2つ含まれる。結果として、2人目が女の子である確率は1/2となる。
このように、2人兄弟の性別に関する問題でも、条件の付し方によって答えが異なってくるが、いずれの問題もベイズの定理を駆使するというものではなさそうである。
3人兄弟の場合
問題を以下の様に拡張する。
これについても以下のように事象を列挙し、確率3/4を得る。
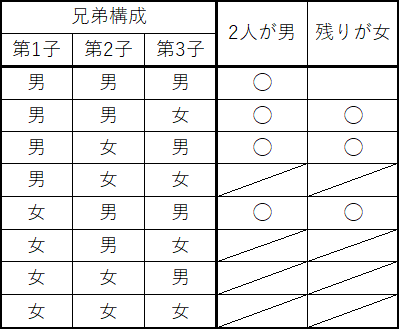
ベイズの定理で表すと以下のようになるが、この場合もまじめに事象のパターンを列挙した考えるほうが素直。
(4) 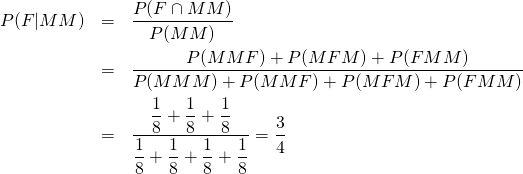
区別なしの場合についてですが、兄、弟の組み合わせについて、答えは2/3になっていますが、気になる点が一つあります。
最初の1人が長子かを気にしない問題であれば、確率が2/3になるのは違和感があります。
理由は、(兄、弟)の場合と(弟、兄)のパターンがあるからです。
男二人ではないパターンが(姉、弟), (兄、妹)というパターンが存在しているのに、
(弟、兄)のパターンを考えないのは違和感を感じます。
ここはどう考えればいいのでしょうか?
質問いただいてありがとうございます。
兄や弟といった順番表現を使ったのがちょっとわかりにくかったかもしれません。
この場合は長子か次子かは問題にしておらず、ただそれぞれの子の性別だけを問題にしています。
したがって、長子が男の場合に「兄」、女の場合に「姉」、次子が男の場合に「弟」、女の場合に「妹」という表現となります。
より問題をシンプルにするなら、「ここに2人の人がいる、ただし姿は見えない。このうち1人が男性だとわかった場合、残る1人が女性である確率は」とでもなるでしょうか。
そうすると、兄・弟はいずれも「男性」に、姉・妹は「女性」に書き換えられます。
その結果、残る1人が女性である確率は2/3になります。
より現実的な問題にするならこういう表現もあります。
「もうすぐ子供を授かる。ただし子供は二卵性双生児だ。そのうち1人は検査で男の子とわかったが、もう1人の性別が判定できない。そのもう1人が女の子である確率は?」
いかがでしょうか。
区別なしの場合、片方が男で確定しているなら
左側を確定とした場合、考えられるパターンは
兄弟
弟兄
兄妹
弟姉
だから、答えは1/2だと思うんだけど、
片方が男だった時点で、姉妹はあり得ないのに
存在するはずのない「姉妹」のパターンを
考慮(表)に入れなければならない理由は何?
提示いただいた4つのパターンのうち、兄弟と弟兄は同じ事象をダブルカウントしています。
ですので組み合わせ数は3通り。
このうち1人が女である事象は妹のケースと姉のケースで2通り。
これより2/3になります。
なお姉妹を表に乗せているのは、最も泥臭く考える道筋として、一旦俎上に乗せた上で対象外としているものです。
最終的に考慮しないので斜線で消しています。
私はこの手の問題が苦手なので、基本に立ち返って整理しました。