ヒストグラムと確率密度曲線を重ねて描くとき

概要

ある確率分布に従っていると思われるデータのヒストグラムと、その確率分布の確率密度曲線を重ねて描きたい場合がある。

RやPythonのmatplotlibではヒストグラムを描く機能が提供されていて、縦軸に度数をとったり、頻度(確率)をとったり選択できる。

縦軸に頻度を選んだ場合は、そのまま確率密度の曲線を重ねて描けばよいが、度数の場合に確率密度を重ねる手順でちょっと戸惑ったので、その手順を記録。

例として、0 ≤ x <1の値が一様な確率で現れる確率分布を考える。その確率密度曲線は以下のようになる。

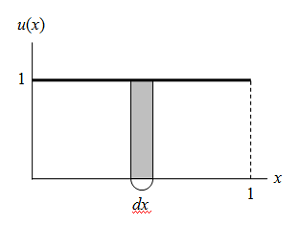
histogram_and_probability_density_1

(1) $\begin{equation*} \int_0^\infty u(x) dx = \int_0^\infty 1 dx = \left[ x \right]_0^\infty = 1 \end{equation*}$

この一様乱数を1000個発生させて、その度数をヒストグラムに表した場合を考える。

仮に各値が実際に全く一様に表れたとすると、グラフは以下のようになり、階級幅によって高さの値が変わってくる。

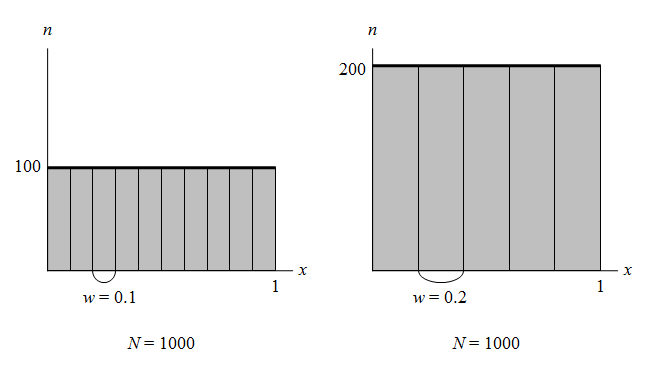
histogram_and_probability_density_2

ヒストグラムの定義を、「ある階級に含まれる度数が階級幅と高さの積」と定義すれば、上の縦軸の値は1000となり、階級幅を変えても高さは変わらないが、縦軸の値を度数とすることで、階級幅によって縦軸の値が変化することになってしまう。

次に、一般の確率密度関数を考える。

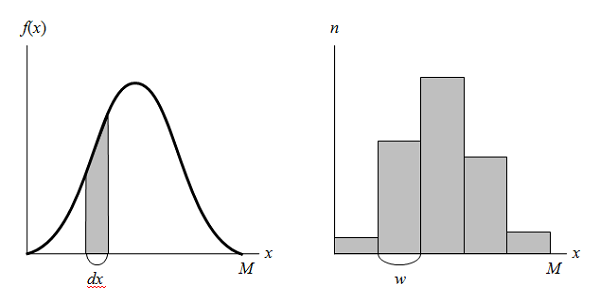
histogram_and_probability_density_3

確率密度関数をf(x)として、区間[x, x + dx)の間の確率P(x)は次式のようになる。

(2) $\begin{equation*} P(x) = f(x) dx \end{equation*}$

両辺に全度数Nをかけると、その値は値xの階級におけるヒストグラムの高さに相当する。

(3) $\begin{equation*} N P(x) = N f(x) dx \end{equation*}$

階級iの高さをh_i、階級幅をw_iとすると、次式は以下のように書ける。

(4) $\begin{equation*} h_i = N w_i f(x) \end{equation*}$

したがって、縦軸が度数表示のヒストグラムに確率密度曲線を重ねて描く場合、階級幅wが一定なら、確率密度関数に総度数Nと階級幅wを乗じて描けばよい。