k-最近傍法 – 回帰

1 概要
2 利用方法
3 実行例
4 各種データに対する適用例

概要

k-最近傍法(k nearest neighbors: knn)による回帰は、テストデータの近傍の訓練データからテストデータの属性値を決定する。その手法は単純で、特段の学習処理はせず、訓練データセットの特徴量と属性値を記憶するのみで、テストデータが与えられたときに近傍点から属性値を決定する。手順は以下の通り。

パッケージをインポートする
特徴量と属性値のデータセットを記憶する
テストデータが与えられたら、特徴量空間の中で近傍点を選ぶ
近傍点の属性値からテストデータの属性値を決定する

パラメーターは近傍点の数で、1以上訓練データの数まで任意に増やすことができる。

利用方法

手順

scikit-learnのKNeighborsRegressorクラスの利用方法は以下の通り。

sklearn.neighborsからKNeighborsRegressorをインポート
コンストラクターの引数に近傍点数n_neighborsを指定して、KNeighborsRegressorのインスタンスを生成
fit()メソッドに訓練データの特徴量と属性値を与えて学習
predict()メソッドにテストデータの特徴量を指定して、属性値を予測
必要に応じて、kneighbors()メソッドでテストデータの近傍点情報を取得

パッケージのインポート

k-最近傍回帰のパッケージは以下でインポートする。

from sklearn.neighbors import KNeighborsRegressor

1	from sklearn.neighbors import KNeighborsRegressor

コンストラクター

KNeighborsClassifier(n_neighbors=n): nは近傍点の数でデフォルトは5。この他の引数に、近傍点を発見するアルゴリズムなどが指定できるようだ。

訓練

fit()メソッドに与える訓練データは、特徴量セットと属性値の2つ。

fit(X, y): Xは訓練データセットの特徴量データで、データ数×特徴量数の2次元配列。yは訓練データセットの属性値データで要素数はデータ数に等しい

予測

テストデータの属性値の予測は、predict()メソッドにテストデータの特徴量を与える。

y = predict(X): Xはテストデータの特徴量データで、データ数×特徴量数の2次元配列。戻り値yは予測された属性値データで要素数はデータ数に等しい。

近傍点の情報

テストデータに対する近傍点の情報を、kneighbors()メソッドで得ることができる。

neigh_dist, neigh_ind = kneighbors(X): テストデータの特徴量Xを引数に与え、近傍点に関する情報を得る。neigh_distは各テストデータから各近傍点までの距離、neigh_indは各テストデータに対する各近傍点のインデックス。いずれも2次元の配列で、テストデータ数×近傍点数の2次元配列となっている。

実行例

以下の例では、n_neighbors=2としてKNeighborsRegressorのインスタンスを準備している。

これに対してfit()メソッドで、2つの特徴量とそれに対する属性値を持つ訓練データを5個与えている。特徴量データX_trainは行数がデータ数、列数が特徴量の数となる2次元配列を想定している。また属性値y_trainは訓練データ数と同じ要素数の1次元配列。

特徴量1	特徴量2	属性値
-2	-3	-1
-1	-1	0
0	1	1
1	2	2
3	3	3

これらの訓練データに対して、テストデータの特徴量X_testとして(-0.5, -2)、(1, 0)の2つを与えた時の出力を見てみる。

import numpy as np
from sklearn.neighbors import KNeighborsRegressor

X_train = np.array(
    [[-2, -3],
     [-1, -1],
     [0, 1],
     [1, 2]])
y_train = np.array([-1, 0, 1, 2])

reg = KNeighborsRegressor(n_neighbors=2)
reg.fit(X_train, y_train)

X_test = np.array([[-0.5, -2], [1, 0]])
y_pred = reg.predict(X_test)

neigh_dist, neigh_ind = reg.kneighbors(X=X_test)

print("X_train=\n{}".format(X_train))
print("y_train={}".format(y_train))
print("X_test=\n{}".format(X_test))
print("y_pred={}".format(y_pred))
print("neighbors' distance=\n{}".format(neigh_dist))
print("neighbors' indicies=\n{}".format(neigh_ind))

import numpy as np

from sklearn.neighbors import KNeighborsRegressor

X_train = np.array(

[[-2, -3],

[-1, -1],

[0, 1],

[1, 2]])

y_train = np.array([-1, 0, 1, 2])

reg = KNeighborsRegressor(n_neighbors=2)

reg.fit(X_train, y_train)

X_test = np.array([[-0.5, -2], [1, 0]])

y_pred = reg.predict(X_test)

neigh_dist, neigh_ind = reg.kneighbors(X=X_test)

print("X_train=\n{}".format(X_train))

print("y_train={}".format(y_train))

print("X_test=\n{}".format(X_test))

print("y_pred={}".format(y_pred))

print("neighbors' distance=\n{}".format(neigh_dist))

print("neighbors' indicies=\n{}".format(neigh_ind))

このコードの実行結果は以下の通り。

X_train=
[[-2 -3]
 [-1 -1]
 [ 0  1]
 [ 1  2]]
y_train=[-1  0  1  2]
[[-0.5 -2. ]
 [ 1.   0. ]]
y_pred=[-0.5  1.5]
neighbors' distance=
[[1.11803399 1.80277564]
 [1.41421356 2.        ]]
neighbors' indicies=
[[1 0]
 [2 3]]

X_train=

[[-2 -3]

[-1 -1]

[ 0 1]

[ 1 2]]

y_train=[-1 0 1 2]

[[-0.5 -2. ]

[ 1. 0. ]]

y_pred=[-0.5 1.5]

neighbors' distance=

[[1.11803399 1.80277564]

[1.41421356 2. ]]

neighbors' indicies=

[[1 0]

[2 3]]

属性値の予測結果については、2つのテストデータに対して2つの属性値0.5と1.5が返されている。

kneighbors()メソッドの戻り値から、1つ目のテストデータにはインデックスが1と0の2つの点とそれぞれへの距離1.118と1.802が、2つ目のテストデータにはインデックスが2と3の点とそれぞれへの距離1.414と2.0が得られる。

1つ目のテストデータ(-0.5, -2)からの距離
- X_train[1]=(-1, -1)→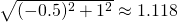 $\sqrt{(-0.5)^2+1^2}\approx 1.118$
- X_train[0]=(-2, -3)→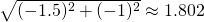 $\sqrt{(-1.5)^2+(-1)^2}\approx 1.802$
2つ目のテストデータ(1, 0)からの距離
- X_train[2]=(0, 1)→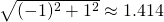 $\sqrt{(-1)^2+1^2}\approx 1.414$
- X_train[3]=(1, 2)→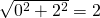 $\sqrt{0^2+2^2}=2$

y_predは、テストデータごとに2つの近傍点の属性値の平均をとっている。

1つ目のテストデータの属性値
- y_train[1]=-1とy_train[0]=0の平均→-0.5
2つ目のテストデータの属性値
- y_train[2]=1とy_train[3]=2の平均→1.5

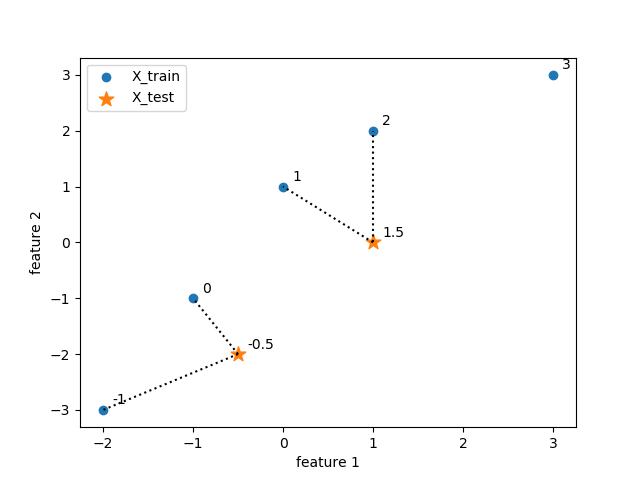
この様子を特徴量平面上に描いたのが以下の図である。各点の数値は、各データの属性値を示している。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.neighbors import KNeighborsRegressor

X_train = np.array(
    [[-2, -3],
     [-1, -1],
     [0, 1],
     [1, 2],
     [3, 3]])
y_train = np.array([-1, 0, 1, 2, 3])

reg = KNeighborsRegressor(n_neighbors=2)
reg.fit(X_train, y_train)

X_test = np.array([[-0.5, -2], [1, 0]])
y_pred = reg.predict(X_test)

neigh_dist, neigh_ind = reg.kneighbors(X=X_test)

fig, ax = plt.subplots()

ax.scatter(X_train[:, 0], X_train[:, 1], label="X_train")
ax.scatter(X_test[:, 0], X_test[:, 1], marker='*', s=120, label="X_test")

for tests, ind in zip(X_test, neigh_ind):
    for neigh in ind:
        ax.plot(
            [tests[0], X_train[neigh][0]], [tests[1], X_train[neigh][1]],
            color='k', linestyle='dotted')

for x, y in zip(X_train, y_train):
    ax.annotate("{}".format(y), xy=(x[0], x[1]), xytext=(x[0]+0.1, x[1]+0.1))
for x, y in zip(X_test, y_pred):
    ax.annotate("{}".format(y), xy=(x[0], x[1]), xytext=(x[0]+0.1, x[1]+0.1))

ax.set_xlabel("feature 1")
ax.set_ylabel("feature 2")
ax.legend()

plt.show()

import numpy as np

import matplotlib.pyplot as plt

from sklearn.neighbors import KNeighborsRegressor

X_train = np.array(

[[-2, -3],

[-1, -1],

[0, 1],

[1, 2],

[3, 3]])

y_train = np.array([-1, 0, 1, 2, 3])

reg = KNeighborsRegressor(n_neighbors=2)

reg.fit(X_train, y_train)

X_test = np.array([[-0.5, -2], [1, 0]])

y_pred = reg.predict(X_test)

neigh_dist, neigh_ind = reg.kneighbors(X=X_test)

fig, ax = plt.subplots()

ax.scatter(X_train[:, 0], X_train[:, 1], label="X_train")

ax.scatter(X_test[:, 0], X_test[:, 1], marker='*', s=120, label="X_test")

for tests, ind in zip(X_test, neigh_ind):

for neigh in ind:

ax.plot(

[tests[0], X_train[neigh][0]], [tests[1], X_train[neigh][1]],

color='k', linestyle='dotted')

for x, y in zip(X_train, y_train):

ax.annotate("{}".format(y), xy=(x[0], x[1]), xytext=(x[0]+0.1, x[1]+0.1))

for x, y in zip(X_test, y_pred):

ax.annotate("{}".format(y), xy=(x[0], x[1]), xytext=(x[0]+0.1, x[1]+0.1))

ax.set_xlabel("feature 1")

ax.set_ylabel("feature 2")

ax.legend()

plt.show()

各種データに対する適用例

waveデータ

TauStation

k-最近傍法 – 回帰

概要

利用方法

手順

パッケージのインポート

コンストラクター

訓練

予測

近傍点の情報

実行例

各種データに対する適用例

コメントを残すコメントをキャンセル

概要

利用方法

手順

パッケージのインポート

コンストラクター

訓練

予測

近傍点の情報

実行例

各種データに対する適用例

コメントを残す コメントをキャンセル

コメントを残すコメントをキャンセル