Logistic回帰～cancer～Pythonではじめる機械学習より

1 モデルの精度
2 学習精度の向上
3 特徴量の係数

モデルの精度

breast_cancerデータセットに対してLogistic回帰モデル、scikit-learnのLogisticRegression適用し、訓練データとテストデータのスコアを計算してみる。

from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression

ds = load_breast_cancer()

X_train, X_test, y_train, y_test = train_test_split(
    ds.data, ds.target, stratify=ds.target, random_state=42)

logreg = LogisticRegression().fit(X_train, y_train)
print("")
print("Training score: {}".format(logreg.score(X_train, y_train)))
print("Test score    : {}".format(logreg.score(X_test, y_test)))

# Training score: 0.9530516431924883
# Test score    : 0.958041958041958

from sklearn.datasets import load_breast_cancer

from sklearn.model_selection import train_test_split

from sklearn.linear_model import LogisticRegression

ds = load_breast_cancer()

X_train, X_test, y_train, y_test = train_test_split(

ds.data, ds.target, stratify=ds.target, random_state=42)

logreg = LogisticRegression().fit(X_train, y_train)

print("")

print("Training score: {}".format(logreg.score(X_train, y_train)))

print("Test score : {}".format(logreg.score(X_test, y_test)))

# Training score: 0.9530516431924883

# Test score : 0.958041958041958

（注）solverに関する警告と計算結果

上のコードを実行したとき、結果は書籍と整合しているが、警告表示が出た

...FutureWarning: Default solver will be changed to 'lbfgs' in 0.22. Specify a solver to silence this warning.
  FutureWarning)
Training score: 0.9530516431924883
Test score    : 0.958041958041958

...FutureWarning: Default solver will be changed to 'lbfgs' in 0.22. Specify a solver to silence this warning.

FutureWarning)

Training score: 0.9530516431924883

Test score : 0.958041958041958

この時点でscikit-learnのバージョンが古く(0.21.3)、将来のデフォルトが変更されるとのこと。そこでインスタンス生成時にデフォルトのソルバーを明示的にsolver='liblinear'と指定して実行すると、警告は出ず値もそのまま。

なお、solver='lbfgs'としてみたところ、計算が収束しない旨の警告が出た。

logreg = LogisticRegression(solver='lbfgs').fit(X_train, y_train)

1	logreg = LogisticRegression(solver='lbfgs').fit(X_train, y_train)

...ConvergenceWarning: lbfgs failed to converge. Increase the number of iterations.
  "of iterations.", ConvergenceWarning)
Training score: 0.9483568075117371
Test score    : 0.951048951048951

...ConvergenceWarning: lbfgs failed to converge. Increase the number of iterations.

"of iterations.", ConvergenceWarning)

Training score: 0.9483568075117371

Test score : 0.951048951048951

そこで収束回数を増やしていったところ、最大回数2000では収束せず、3000で収束し、警告は出なくなった。

logreg = LogisticRegression(solver='lbfgs', max_iter=3000).fit(X_train, y_train)

1	logreg = LogisticRegression(solver='lbfgs', max_iter=3000).fit(X_train, y_train)

Training score: 0.9577464788732394
Test score    : 0.958041958041958

1 2	Training score: 0.9577464788732394 Test score : 0.958041958041958

その後、scikit-learnのバージョンを0.23.0にアップグレードしたところ、デフォルトで警告は表示されず、収束回数に関する警告が同じように出て、結果も再現された。以下、ソルバーとしてliblinearを明示的に指定し、random_stateの値も書籍と同じ値として確認する。

学習精度の向上

先のC=1.0とliblinearによるスコアは、訓練データに対して0.953、テストデータに対して0.958と両方に対して高い値となっている。ここで、訓練データとテストデータのスコアが近いということは、適合不足の可能性がある。そこでC=100と値を大きくして、より柔軟なモデルにしてみる（柔軟なモデルとは、正則化を弱めて訓練データによりフィットしやすくしたモデル）。

logreg100 = LogisticRegression(C=100, solver='liblinear').fit(X_train, y_train)
print("Training score: {}".format(logreg100.score(X_train, y_train)))
print("Test score    : {}".format(logreg100.score(X_test, y_test)))

# Training score: 0.9788732394366197
# Test score    : 0.965034965034965

logreg100 = LogisticRegression(C=100, solver='liblinear').fit(X_train, y_train)

print("Training score: {}".format(logreg100.score(X_train, y_train)))

print("Test score : {}".format(logreg100.score(X_test, y_test)))

# Training score: 0.9788732394366197

# Test score : 0.965034965034965

訓練データ、テストデータともそれぞれ若干向上している。なお、Cの値を1000、10000ともっと大きくしてもスコアはほとんど変わらない。

今度は逆に、Cの値を1.0より小さくして正則化を強めてみると、訓練データ、テストデータ両方に対するスコアが下がってしまう。

logreg001 = LogisticRegression(C=0.01, solver='liblinear').fit(X_train, y_train)
print("Training score: {}".format(logreg001.score(X_train, y_train)))
print("Test score    : {}".format(logreg001.score(X_test, y_test)))

# Training score: 0.9342723004694836
# Test score    : 0.9300699300699301

logreg001 = LogisticRegression(C=0.01, solver='liblinear').fit(X_train, y_train)

print("Training score: {}".format(logreg001.score(X_train, y_train)))

print("Test score : {}".format(logreg001.score(X_test, y_test)))

# Training score: 0.9342723004694836

# Test score : 0.9300699300699301

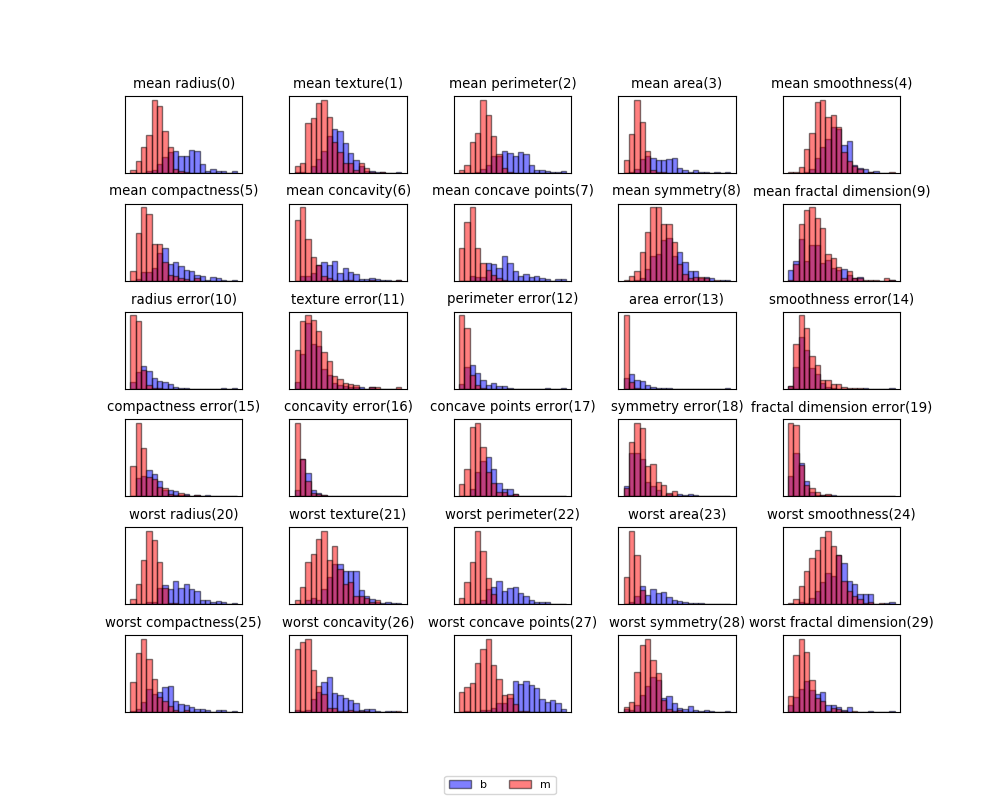
Cを変化させたときの学習率曲線は以下の通り。Cが10より小さいところでは正則化が強く学習不足、そこを超えると学習率が頭打ちで、学習率の改善はそれほど顕著ではない。Logistic回帰モデルの学習率曲線のバリエーションについては、こちらでまとめている。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression

C_pow_min = -4
C_pow_max = 3
C_pow_num = 100
Cs_pows = np.linspace(C_pow_min, C_pow_max, C_pow_num)
Cs = 10**Cs_pows

ds = load_breast_cancer()

X_train, X_test, y_train, y_test = train_test_split(
    ds.data, ds.target, stratify=ds.target, random_state=42)

fig, ax = plt.subplots()

score_trains = np.empty(0)
score_tests = np.empty(0)

for C in Cs:
    logreg = LogisticRegression(C=C, solver='liblinear').fit(X_train, y_train)
    score_trains = np.append(score_trains, logreg.score(X_train, y_train))
    score_tests = np.append(score_tests, logreg.score(X_test, y_test))

ax.plot(Cs, score_trains, label="Training")
ax.plot(Cs, score_tests, label="Test")

ax.set_xscale('log')
ax.legend()

plt.show()

import numpy as np

import matplotlib.pyplot as plt

from sklearn.datasets import load_breast_cancer

from sklearn.model_selection import train_test_split

from sklearn.linear_model import LogisticRegression

C_pow_min = -4

C_pow_max = 3

C_pow_num = 100

Cs_pows = np.linspace(C_pow_min, C_pow_max, C_pow_num)

Cs = 10**Cs_pows

ds = load_breast_cancer()

X_train, X_test, y_train, y_test = train_test_split(

ds.data, ds.target, stratify=ds.target, random_state=42)

fig, ax = plt.subplots()

score_trains = np.empty(0)

score_tests = np.empty(0)

for C in Cs:

logreg = LogisticRegression(C=C, solver='liblinear').fit(X_train, y_train)

score_trains = np.append(score_trains, logreg.score(X_train, y_train))

score_tests = np.append(score_tests, logreg.score(X_test, y_test))

ax.plot(Cs, score_trains, label="Training")

ax.plot(Cs, score_tests, label="Test")

ax.set_xscale('log')

ax.legend()

plt.show()

特徴量の係数

L2正則化の場合

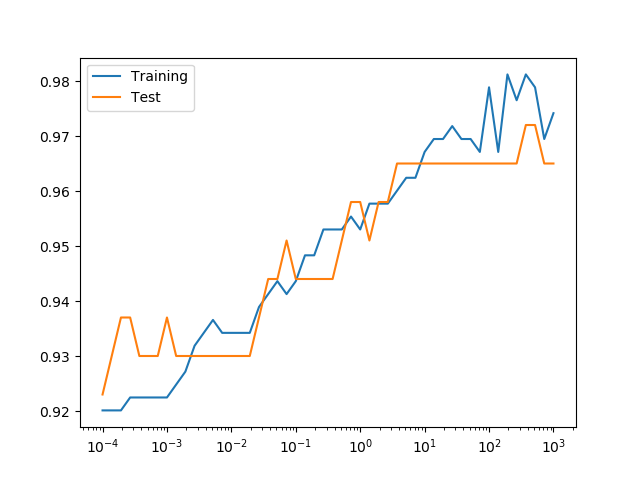
breast_cancerデータセットに対してLogisticRegressionを学習させた場合の、30個の特徴量に対する係数をプロットする。liblinearソルバーで、デフォルトでL2正則化を行っている。Cの値が大きいほど正則化の効果が弱く、係数の絶対値が大きくなっている。

書籍で注意喚起しているのは3番目の特徴量mean perimeterで、モデルによって正負が入れ替わることから、クラス分類に対する信頼性を問題にしている。

ここで書籍について以下の点が気になった。

logreg001のインスタンス生成時にC=0.01としているが、凡例で”C=0.001″としている（グラフの結果はあまり変わらない）
logreg100でC=100とすると、書籍にあるような結果にならない（worst concave pointsが-8以下になるなど、分布が大幅に変わってくる）
C=20とすると、概ね書籍と同じ分布になる（若干異なる部分は残る）

いずれにしても”Pythonではじめる機械学習”は、入門者にとってとてもありがたいきっかけを提供してくれる良著であることに変わりはない。

import numpy as np
import matplotlib.pyplot as plt
import matplotlib.patches as pch
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression

ds = load_breast_cancer()

X_train, X_test, y_train, y_test = train_test_split(
    ds.data, ds.target, stratify=ds.target, random_state=42)

logreg1 = LogisticRegression(solver='liblinear').fit(X_train, y_train)
logreg20 = LogisticRegression(C=20, solver='liblinear').fit(X_train, y_train)
logreg001 = LogisticRegression(C=0.01, solver='liblinear').fit(X_train, y_train)

x_scatter = np.linspace(0, 1, len(ds.feature_names))

fig, ax = plt.subplots(figsize=(6.4, 6.4))

ax.scatter(x_scatter, logreg1.coef_, marker='o', c='grey', s=100,
    label="C=1.0")
ax.scatter(x_scatter, logreg001.coef_, marker='1', c='blue', s=100,
    label="C=0.01")
ax.scatter(x_scatter, logreg20.coef_, marker='2', c='red', s = 100,
    label="C=20")
ax.plot([0, 1], [0, 0], c='k', zorder=-100)
ax.add_patch(pch.Arrow(2/30, -4, 0, 3, width=1/30))

ax.set_xticks(x_scatter)
ax.set_xticklabels(ds.feature_names, rotation=90)
ax.set_xlim(0, 1)
ax.legend()

fig.subplots_adjust(bottom=0.3)

plt.show()

import numpy as np

import matplotlib.pyplot as plt

import matplotlib.patches as pch

from sklearn.datasets import load_breast_cancer

from sklearn.model_selection import train_test_split

from sklearn.linear_model import LogisticRegression

ds = load_breast_cancer()

X_train, X_test, y_train, y_test = train_test_split(

ds.data, ds.target, stratify=ds.target, random_state=42)

logreg1 = LogisticRegression(solver='liblinear').fit(X_train, y_train)

logreg20 = LogisticRegression(C=20, solver='liblinear').fit(X_train, y_train)

logreg001 = LogisticRegression(C=0.01, solver='liblinear').fit(X_train, y_train)

x_scatter = np.linspace(0, 1, len(ds.feature_names))

fig, ax = plt.subplots(figsize=(6.4, 6.4))

ax.scatter(x_scatter, logreg1.coef_, marker='o', c='grey', s=100,

label="C=1.0")

ax.scatter(x_scatter, logreg001.coef_, marker='1', c='blue', s=100,

label="C=0.01")

ax.scatter(x_scatter, logreg20.coef_, marker='2', c='red', s = 100,

label="C=20")

ax.plot([0, 1], [0, 0], c='k', zorder=-100)

ax.add_patch(pch.Arrow(2/30, -4, 0, 3, width=1/30))

ax.set_xticks(x_scatter)

ax.set_xticklabels(ds.feature_names, rotation=90)

ax.set_xlim(0, 1)

ax.legend()

fig.subplots_adjust(bottom=0.3)

plt.show()

L1正則化の場合

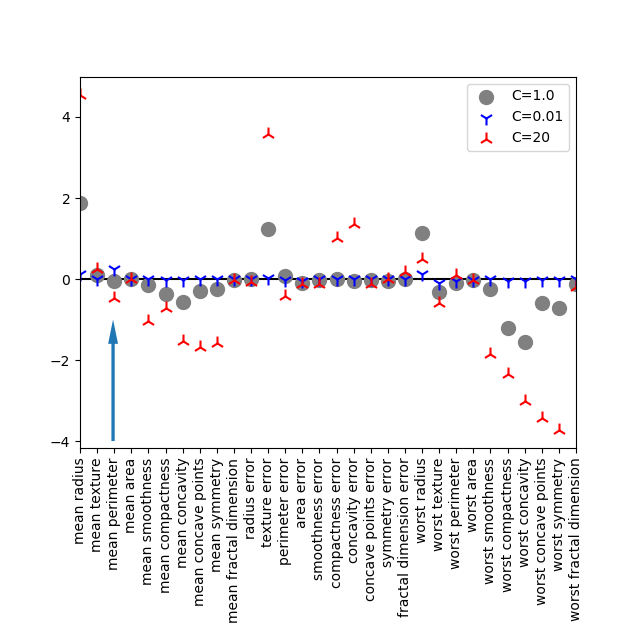
ソルバーを同じliblinearとして、penalty='l1'と明示的に指定する。今回はL2正則化の時と違って、C=0.001はコード中に明示され、C=100としてスコアの計算結果まで合う。ただしset_ylim()によって表示範囲を制限しており、C=100に対するいくつかの点が枠外にある。

L1正則化によって、多くの係数がゼロとなり、少ない特徴量によるシンプルなモデルでそれなりのスコアを出している。

logreg1 = LogisticRegression(solver='liblinear', penalty='l1').\
    fit(X_train, y_train)
logreg100 = LogisticRegression(C=100, solver='liblinear', penalty='l1').\
    fit(X_train, y_train)
logreg001 = LogisticRegression(C=0.001, solver='liblinear', penalty='l1').\
    fit(X_train, y_train)
print("C=0.001")
print(" Training score: {:5.3f}".format(logreg001.score(X_train, y_train)))
print(" Test score    : {:5.3f}".format(logreg001.score(X_test, y_test)))
print("C=1")
print(" Training score: {:5.3f}".format(logreg1.score(X_train, y_train)))
print(" Test score    : {:5.3f}".format(logreg1.score(X_test, y_test)))
print("C=100")
print(" Training score: {:5.3f}".format(logreg100.score(X_train, y_train)))
print(" Test score    : {:5.3f}".format(logreg100.score(X_test, y_test)))

# C=0.001
#  Training score: 0.913
#  Test score    : 0.923
# C=1
#  Training score: 0.960
#  Test score    : 0.958
# C=100
#  Training score: 0.986
#  Test score    : 0.979

logreg1 = LogisticRegression(solver='liblinear', penalty='l1').\

fit(X_train, y_train)

logreg100 = LogisticRegression(C=100, solver='liblinear', penalty='l1').\

fit(X_train, y_train)

logreg001 = LogisticRegression(C=0.001, solver='liblinear', penalty='l1').\

fit(X_train, y_train)

print("C=0.001")

print(" Training score: {:5.3f}".format(logreg001.score(X_train, y_train)))

print(" Test score : {:5.3f}".format(logreg001.score(X_test, y_test)))

print("C=1")

print(" Training score: {:5.3f}".format(logreg1.score(X_train, y_train)))

print(" Test score : {:5.3f}".format(logreg1.score(X_test, y_test)))

print("C=100")

print(" Training score: {:5.3f}".format(logreg100.score(X_train, y_train)))

print(" Test score : {:5.3f}".format(logreg100.score(X_test, y_test)))

# C=0.001

# Training score: 0.913

# Test score : 0.923

# C=1

# Training score: 0.960

# Test score : 0.958

# C=100

# Training score: 0.986

# Test score : 0.979

係数の符号と選択確率について

ターゲットのクラスは、malignant(悪性)が0、benign(良性)が1で、係数が正の場合は良性となる確率を上げる方向に、負の場合は悪性となる確率を上げる方向に効くことになる。

ここでL2正則化のworst concavityを見てみると、負～0の値をとっているが、元のデータを俯瞰すると良性の集団の方が全体的に高い値を示していて矛盾している。一方、L1正則化の場合は、C=0.001で全ての係数がゼロとなっていて、結果に影響していないことを示唆している。

L1正則化で正則化の程度を弱めて、C=1, 0.5, 0.1としてみると、worst concavityは結局ゼロとなるが、worst textureは一貫して負の値を維持している。この傾向はarea errorにも僅かだが見られる。

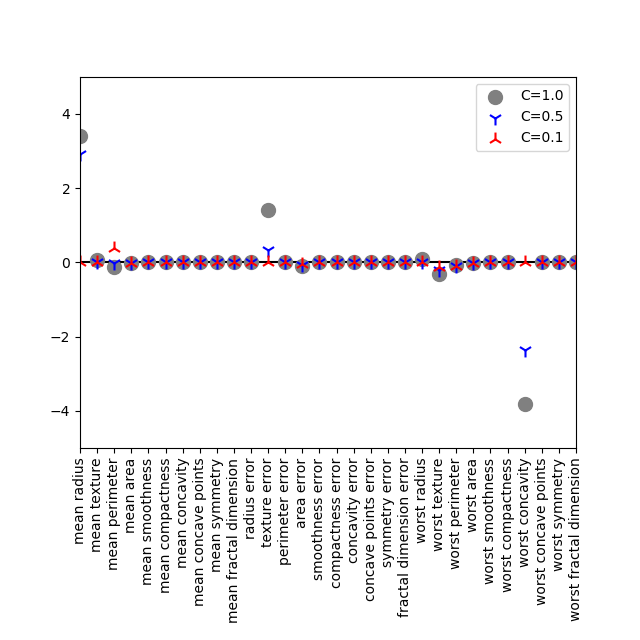
cancerデータを俯瞰してみると、worst textureは良性・悪性の分布がかなり重なっていて、悪性のデータのボリュームが大きい。area errorも両クラスのデータが近く、値が小さく、良性のデータ量が卓越している。

ヒストグラムを見る限りほとんどの特性量の値が大きいときに良性を示唆しているようみ見えるが、Logistic回帰の結果からは、多くの特性量が効いておらず、中には分布からの推測と逆の傾向を示す。

TauStation

Logistic回帰～cancer～Pythonではじめる機械学習より

モデルの精度

学習精度の向上

特徴量の係数

L2正則化の場合

L1正則化の場合

係数の符号と選択確率について

コメントを残すコメントをキャンセル

モデルの精度

学習精度の向上

特徴量の係数

L2正則化の場合

L1正則化の場合

係数の符号と選択確率について

コメントを残す コメントをキャンセル

コメントを残すコメントをキャンセル