考え方
時刻制御(time driven)による待ち行列の計算の考え方は次の通り。
- 時刻t0から始めて、以下時間間隔Δtずつ増やしながら計算を進めていく
- ある時刻で一様乱数の値がλΔtより小さければ到着が発生
- 新たにトランザクションを生成し、到着時刻を記録し、システムに投入する
- ある時刻で到着が発生せず、システムにトランザクションがある場合、一様乱数の値がμΔtより小さければサービスが終了
- サービス中のトランザクションのサービスを終了させ、終了時刻を記録する
- このとき待ち行列にトランザクションがあれば、先頭のトランザクションのサービスを開始し、サービス開始時刻を記録する
- 予め設定していた時刻(またはトランザクション数)に達したら終了
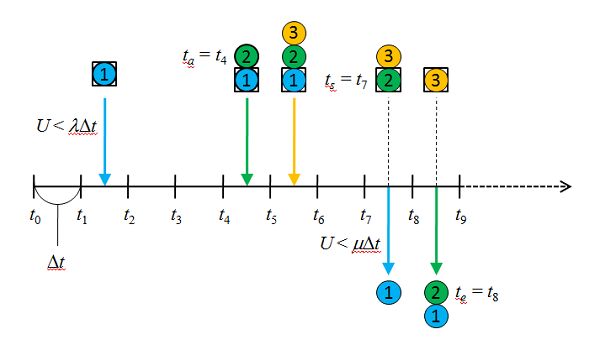
たとえば上の図でトランザクション②に注目すると、
- 時刻t4でトランザクションが発生
- t7でトランザクション①のサービスが終了し、②のサービスが開始
- t8でサービス終了
イベント制御のケースではRを用いたが、今回はPythonを使う。なおM/M/1待ち行列の解析的アプローチはこちら。
待ち行列システムのクラスをつくり、システムの外からはトランザクションの到着、サービス終了の操作を行うだけで、内部的に処理が進むようにする。
クラス構成
待ち行列システムを表すQueueSystemクラス、システムのサービス窓口を表すServiceクラス、システム中の1つのトランザクションを表すTransactionクラスから構成される。システム中の待ち行列はインスタンス変数のリストとして持つ。
M/M/1型の行列システムとして、QueueSystemクラスは1つのServiceオブジェクトと1つの待ち行列リストをメンバーに持つ。
トランザクションの到着の指示が出るとTransactionオブジェクトが生成され、システムに登録される。
その一方で実行中のサービス終了の指示が出るとサービスを受けているトランザクションが解放される。
各Transactionオブジェクトに対して、システムの到着、サービスの開始、サービスの終了の時刻が自動的に登録される。
Transactionクラス
- 識別子としての整数値のindexのほか、到着・サービス開始・サービス終了の時刻、到着時のシステム内トランザクション数と待ち行列長をメンバーとして持つ
- これらのメンバーに対しては直接アクセスして参照・代入する
- このクラスのオブジェクトの文字列表現を
__str__メソッドで実装している
|
1 2 3 4 5 6 7 8 9 10 11 12 |
class Transaction: def __init__(self, index, arrive_time): self.index = index self.arrive_time = arrive_time self.start_time = 0 self.end_time = 0 self.transaction_number_when_arrived = 0 self.queue_length_when_arrived = 0 def __str__(self): return "<{}:{},{},{}>".format( self.index, self.arrive_time, self.start_time, self.end_time) |
Serviceクラス
- privateなメンバ_transactionを持ち、これはサービス中のトランザクションを保持する
- サービス中のトランザクションがない場合はNone
- サービス窓口が空いているか(vacant)、サービス中か(occupied)を判定するメソッドを持つ
- サービス中のトランサクションへの参照を返す
transaction_in_service()メソッドを持つ - サービス開始時の処理を行うstart()メソッドを持つ
- サービスを開始する
Transactionオブジェクトとサービス開始時刻を指定する
- サービスを開始する
- サービス終了時の処理を行うend()メソッドを持つ
- サービス終了時刻を指定し、サービス中のTransactionオブジェクトにその時刻を設定し、オブジェクトへの参照を返す
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
class Service: def __init__(self): self._transaction = None def is_vacant(self): return self._transaction is None def is_occupied(self): return self._transaction is not None def transaction_in_service(self): return self._transaction def start(self, transaction, time): transaction.start_time = time self._transaction = transaction def end(self, time): transaction = self._transaction transaction.end_time = time self._transaction = None return transaction |
QueueSystemクラス
メンバとなるインスタンス変数は4つ
- 待ち行列リスト
_queue - サービス窓口オブジェクト
_service - 到着済みのトランザクションを登録する
_arrived_transaction_list - サービス完了済みのトランザクションを登録する
_departed_transaction_list
getter系のメソッドは
- システム中にあるトランザクション数を返す
transaction_number_in_system() - 待ち行列長を返す
queue_length() - システム中にあるトランザクションへの参照を返す
transaction_in_service() - 待ち行列中にあるトランザクションへの参照を返す
transaction_in_queue() - 到着済みのトランザクション数を返す
arrived_transaction_number() - 完了済みのトランザクション数を返す
departed_transaction_number() - 到着済みのトランザクションのn番目を返す
arrived_transaction() - 完了済みのトランザクションのn番目を返す
departed_transaction()
システムを操作するメソッドは
- システムに到着したトランザクションを登録する
arrive() - サービスが終了したトランザクションをシステムから取り出す
depart()
システムの状態を表示するメソッドとして以下の2つを実装している。
- システムの現在の状態を表示する
display_current_status() - サービスを完了したトランザクション群の各パラメータを表示する
display_transaction_summary()
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 |
class QueueSystem: def __init__(self): self._queue = [] self._service = Service() self._arrived_transaction_list = [] self._departed_transaction_list = [] def transaction_number_in_system(self): return (len(self._queue) + (1 if self._service.is_occupied() else 0)) def queue_length(self): return len(self._queue) def transaction_in_service(self): return self._service.transaction_in_service() def transaction_in_queue(self, n): return self._queue[n] def arrived_transaction_number(self): return len(self._arrived_transaction_list) def departed_transaction_number(self): return len(self._departed_transaction_list) def arrived_transaction(self, n): return self._arrived_transaction_list[n] def departed_transaction(self, n): return self._departed_transaction_list[n] def arrive(self, transaction): self._arrived_transaction_list.append(transaction) transaction.transaction_number_when_arrived = \ self.transaction_number_in_system() transaction.queue_length_when_arrived = self.queue_length() if self._service.is_vacant(): self._service.start(transaction, transaction.arrive_time) else: self._queue.append(transaction) def depart(self, time): departing_transaction = self._service.end(time) self._departed_transaction_list.append(departing_transaction) if len(self._queue) > 0: waiting_transaction = self._queue.pop(0) self._service.start(waiting_transaction, time) def display_current_status(self): print() print("--- Queue System Status ---") print("arrived :{0:5d}".format(self.arrived_transaction_number())) print("departed:{0:5d}".format(self.departed_transaction_number())) print("[Service]") if self.transaction_number_in_system() > 0: print(' ' + str(self.transaction_in_service())) print("[Queue]") if self.queue_length() > 0: for n in range(0, self.queue_length()): print(self.transaction_in_queue(n)) def display_transaction_summary(self): print() print("---------------------------- " \ "All Transaction Summary " \ "---------------------------") print( " index arrive start end" \ " trs num que len wait time trs time") for tr in self._departed_transaction_list: print("{0:10d}{1:10.2f}{2:10.2f}{3:10.2f}" \ "{4:10d}{5:10d}{5:10.2f}{6:10.2f}".format( tr.index, tr.arrive_time, tr.start_time, tr.end_time, tr.transaction_number_when_arrived, tr.queue_length_when_arrived, tr.start_time - tr.arrive_time, tr.end_time - tr.arrive_time)) |
動作テスト
上記のクラス群を使って以下を実行。規則正しく刻まれた時刻に4つのトランザクションが到着し、その後規則正しくサービスが終了していく様子と、その結果を表示させている。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 |
trs = [] for n in range(1, 10): trs.append(Transaction(n, n*10)) system = QueueSystem() system.display_current_status() system.arrive(trs[0]) system.display_current_status() system.arrive(trs[1]) system.display_current_status() system.arrive(trs[2]) system.display_current_status() system.arrive(trs[3]) system.display_current_status() system.depart(45) system.display_current_status() system.depart(55) system.display_current_status() system.depart(65) system.display_current_status() system.depart(75) system.display_current_status() print() system.display_transaction_summary() print() print("-- arrived --") na = system.arrived_transaction_number() for i in range(0, na): print(system.arrived_transaction(i)) print() print("-- departed --") na = system.departed_transaction_number() for i in range(0, na): print(system.departed_transaction(i)) |
実行結果は以下の通りで、意図したようにトランザクションの到着に従って登録され、終了指示によって待ち行列・サービス状況が変化している。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 |
--- Queue System Status --- arrived : 0 departed: 0 [Service] [Queue] --- Queue System Status --- arrived : 1 departed: 0 [Service] <1:10,10,0> [Queue] --- Queue System Status --- arrived : 2 departed: 0 [Service] <1:10,10,0> [Queue] <2:20,0,0> --- Queue System Status --- arrived : 3 departed: 0 [Service] <1:10,10,0> [Queue] <2:20,0,0> <3:30,0,0> --- Queue System Status --- arrived : 4 departed: 0 [Service] <1:10,10,0> [Queue] <2:20,0,0> <3:30,0,0> <4:40,0,0> --- Queue System Status --- arrived : 4 departed: 1 [Service] <2:20,45,0> [Queue] <3:30,0,0> <4:40,0,0> --- Queue System Status --- arrived : 4 departed: 2 [Service] <3:30,55,0> [Queue] <4:40,0,0> --- Queue System Status --- arrived : 4 departed: 3 [Service] <4:40,65,0> [Queue] --- Queue System Status --- arrived : 4 departed: 4 [Service] [Queue] -----------------------=---- All Transaction Summary --------------------------- index arrive start end trs num que len wait time trs time 1 10.00 10.00 45.00 0 0 0.00 0.00 2 20.00 45.00 55.00 1 0 0.00 25.00 3 30.00 55.00 65.00 2 1 1.00 25.00 4 40.00 65.00 75.00 3 2 2.00 25.00 -- arrived -- <1:10,10,45> <2:20,45,55> <3:30,55,65> <4:40,65,75> -- departed -- <1:10,10,45> <2:20,45,55> <3:30,55,65> |
時刻制御の実装
考え方
概略の流れは以下の通り。
- 計算に必要なパラメータを設定する
- 到着率 λ
- サービス率 μ
- 計算時間範囲 t_max
- 計算時間間隔 dt
- 時刻tが0からt_maxになるまでdtずつ増やしながら以下を実行(以下、randは[0, 1)の一様乱数値)
- λdt < randならトランザクションが一つ到着して次の時間ステップへ
- サービス中のトランザクションがあって、μdt < randならトランザクションが一つ終了して次の時間ステップへ
- トランザクションのサマリーを表示
テスト実行
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
import numpy.random as rnd lmd = 1 / 10 mu = 1 / 8 t_max = 100 dt = 0.5 system = QueueSystem() nstep = int(t_max / dt) index = 0 for it in range(0, nstep): t = it * dt if rnd.rand() < lmd * dt: transaction = Transaction(index, t) system.arrive(transaction) index += 1 continue if system.transaction_number_in_system() > 0: if rnd.rand() < mu * dt: transaction = system.depart(t) continue system.display_transaction_summary() |
実行結果は以下の通り。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
-----------------------=---- All Transaction Summary --------------------------- index arrive start end trs num que len wait time trs time 0 1.00 1.00 12.50 0 0 0.00 0.00 1 2.50 12.50 15.00 1 0 0.00 10.00 2 5.00 15.00 17.50 2 1 1.00 10.00 3 10.00 17.50 24.00 3 2 2.00 7.50 4 20.00 24.00 37.00 1 0 0.00 4.00 5 25.00 37.00 39.50 1 0 0.00 12.00 6 30.00 39.50 41.00 2 1 1.00 9.50 7 34.50 41.00 46.00 3 2 2.00 6.50 8 52.50 52.50 67.50 0 0 0.00 0.00 9 68.50 68.50 69.50 0 0 0.00 0.00 10 70.00 70.00 80.00 0 0 0.00 0.00 11 72.00 80.00 91.00 1 0 0.00 8.00 12 81.00 91.00 93.50 1 0 0.00 10.00 |
実行結果
到着時間間隔の分布の確認
およそ1000個のデータを発生させるため、観測時間を10000秒にして計算し、到着したトランザクションの到着時間間隔を確認した。確認部分のコードの未以下に示す。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
arrival_interval = [] for i in range(0, system.departed_transaction_number() - 1): transaction = system.departed_transaction(i) next_transaction = system.departed_transaction(i + 1) arrival_interval.append(next_transaction.arrive_time - transaction.arrive_time) range_max = 60 bins_num = 10 n = len(arrival_interval) x = [t for t in range(0, range_max)] plt.plot(x, [lmd*exp(-lmd*t) for t in x]) plt.hist(arrival_interval, range=(0, range_max), bins=bins_num, normed=True) plt.show() |
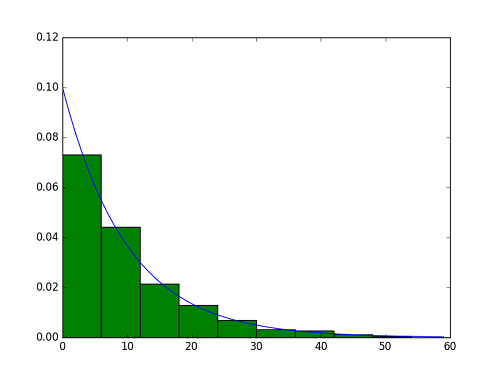
実行結果は以下の通りで、指数分布の理論値とよく合っている。
matplotlibのhist関数はnormed=Trueとした場合に期待した動作をしないことがあるが、このケースではうまくいっている。
平均トランザクション数・平均待ち行列長など
10000秒の観測時間で、システム内の平均トランザクション数、平均待ち行列長と、それらに対する平均応答時間、平均待ち時間について計算し、λ、μから計算される理論値と比較した。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 |
mean_transaction_number_in_system = 0 mean_queue_length = 0 mean_wait_time = 0 mean_transaction_time = 0 n = system.departed_transaction_number() for i in range(n): tr = system.departed_transaction(i) mean_transaction_number_in_system += tr.transaction_number_when_arrived mean_queue_length += tr.queue_length_when_arrived mean_transaction_time += tr.end_time - tr.arrive_time mean_wait_time += tr.start_time - tr.arrive_time mean_transaction_number_in_system /= n mean_queue_length /= n mean_transaction_time /= n mean_wait_time /= n rho = lmd / mu Lt = rho / (1 - rho) Lq = rho * rho / (1 - rho) Tt = Lt / lmd Tq = Lq / lmd print("transaction number:" + str(n)) fmtstr = "{0:10s}{1:15.2f}{2:15.2f}" print(" observed calculated") print(fmtstr.format("trs num", mean_transaction_number_in_system, Lt)) print(fmtstr.format("queue len", mean_queue_length, Lq)) print(fmtstr.format("trs time", mean_transaction_time, Tt)) print(fmtstr.format("wait time", mean_wait_time, Tq)) |
計算結果は以下の通りで、かなり整合している。
|
1 2 3 4 5 6 |
transaction number:990 observed calculated trs num 0.99 1.00 queue len 0.48 0.50 trs time 10.19 10.00 wait time 5.09 5.00 |
各実行結果の傾向
およそ1000個のデータに相当する10000時間単位まで、時間ステップ0.1で計算を行い、理論値との違いを確認した。
ρ = 0.5のケース
λ = 1/10、μ = 1/5、ρ = 0.5のケース。平均トランザクション数と平均待ち行列長の理論値は、L = 1、Lq = 0.5で、これらに対する待ち時間はT = 10、Tw = 5。
トランザクション数に関する計算結果は理論値とかなりよく合っている。
| L | T | 1/λ | |
| 1 | 1.19667319 | 11.32504892 | 9.46377759 |
| 2 | 1.14047151 | 10.43113949 | 9.14633938 |
| 3 | 1.01360544 | 9.81409135 | 9.68235860 |
| 4 | 1.10038241 | 10.86032505 | 9.86959165 |
| 5 | 1.21322160 | 11.32597765 | 9.33545664 |
| 6 | 0.91197544 | 9.24390993 | 10.13613912 |
| 7 | 0.92921236 | 9.52532403 | 10.25096570 |
| 8 | 0.92452830 | 9.96117180 | 10.77432870 |
| 9 | 0.87450199 | 9.12868526 | 10.43872440 |
| 10 | 0.93159923 | 9.19017341 | 9.86494311 |
| AVG | 1.02361714 | 10.08058469 | 9.89626249 |
| STD | 0.12142639 | 0.81382679 | 0.48579815 |
待ち行列長は若干ばらつきが大きくなっている。
| Lq | Tq | 1/λ | |
| 1 | 0.67906067 | 6.27358121 | 9.23861664 |
| 2 | 0.63555992 | 5.54204322 | 8.71993819 |
| 3 | 0.50728863 | 4.87269193 | 9.60536397 |
| 4 | 0.57456979 | 5.73049713 | 9.97354408 |
| 5 | 0.63314711 | 6.07476723 | 9.59455888 |
| 6 | 0.42169908 | 4.29559877 | 10.18640773 |
| 7 | 0.46660020 | 4.73389831 | 10.14551282 |
| 8 | 0.44985104 | 5.01837140 | 11.15562921 |
| 9 | 0.38844622 | 4.27151394 | 10.99641011 |
| 10 | 0.44797688 | 4.41705202 | 9.85999996 |
| AVG | 0.52041995 | 5.12300151 | 9.94759816 |
| STD | 0.09722322 | 0.70052360 | 0.70110321 |
ρ = 0.9のケース
λ = 1/10、μ = 1/9、ρ = 0.9のケース。平均トランザクション数と平均待ち行列長の理論値は、L = 9、Lq = 8.1で、これらに対する待ち時間はT = 90、Tw = 81。
トランザクション数に関する計算結果は、理論値の周りに大きくばらついている。
| L | T | 1/λ | |
| 1 | 7.59815951 | 76.92402863 | 10.12403445 |
| 2 | 7.72051010 | 86.82890542 | 11.24652443 |
| 3 | 7.96595331 | 80.47908560 | 10.10288191 |
| 4 | 5.22616633 | 54.55070994 | 10.43799728 |
| 5 | 5.11700000 | 52.88450000 | 10.33505961 |
| 6 | 8.65760322 | 89.70845921 | 10.36181226 |
| 7 | 6.19872476 | 65.22922423 | 10.52300703 |
| 8 | 10.88111888 | 110.54815185 | 10.15963092 |
| 9 | 8.41194645 | 86.59763131 | 10.29460088 |
| 10 | 18.80710660 | 193.82274112 | 10.30582456 |
| AVG | 8.65842892 | 89.75734373 | 10.38913733 |
| STD | 3.75303129 | 38.38222105 | 0.31302798 |
待ち行列長の計算結果もかなりばらついている。
| Lq | Tq | 1/λ | |
| 1 | 6.71165644 | 67.97975460 | 10.12861061 |
| 2 | 6.82678002 | 77.21158342 | 11.31010274 |
| 3 | 7.02334630 | 71.38190661 | 10.16351801 |
| 4 | 4.35902637 | 45.64036511 | 10.47031177 |
| 5 | 4.22800000 | 44.04650000 | 10.41780984 |
| 6 | 7.72205438 | 80.19728097 | 10.38548513 |
| 7 | 5.31880978 | 56.14229543 | 10.55542457 |
| 8 | 9.95704296 | 101.38201798 | 10.18194040 |
| 9 | 7.49742533 | 77.17693100 | 10.29379122 |
| 10 | 17.87005076 | 184.15197970 | 10.30506193 |
| AVG | 7.75141923 | 80.53106148 | 10.42120562 |
| STD | 3.73662161 | 38.18242499 | 0.32416633 |
ρが高くなる(混雑してくる)と計算結果と理論値のかい離が大きくなるのは、(言語が異なるとはいえ)同じ傾向。時刻制御では計算時間間隔を0.1でも試してみたが、あまり傾向は変わらない。