mplot3d.Axes3D – 3次元グラフの概要

1 概要
2 各種描画処理

概要

Pythonのライブラリーを使った3次元グラフ表示の概要をまとめる。大きな流れは以下の通り。

# ライブラリーの読み込み
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

# Axes3Dオブジェクトの生成
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')

# 各種描画処理

# プロットの表示
plt.show()

# ライブラリーの読み込み

import numpy as np

import matplotlib.pyplot as plt

from mpl_toolkits.mplot3d import Axes3D

# Axes3Dオブジェクトの生成

fig = plt.figure()

ax = fig.add_subplot(111, projection='3d')

# 各種描画処理

# プロットの表示

plt.show()

Axes3Dオブジェクトの生成で以下のようにしている例もあるが、古いバージョンのものであり、matplotlibのチュートリアルでは上記の方法を推奨している。

fig = plt.figure()
ax = Axes3D(fig)

1 2	fig = plt.figure() ax = Axes3D(fig)

なお、FigureオブジェクトとAxes3Dオブジェクトを1行で生成する方法がこちらに紹介されている。この方法だと1行ですみ、複数のAxes3Dを一度に生成できる。

fig, ax = plt.subplots(subplot_kw=dict(projection='3d'))

1	fig, ax = plt.subplots(subplot_kw=dict(projection='3d'))

各種描画処理

`scatter`～点の表示

2次元のscatterと同じで、x, y, zの3次元の座標を配列で指定。以下の例では立方体の8つの頂点を3次元空間内に表示する。

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

x = [1, 1, 2, 2, 1, 1, 2, 2]
y = [1, 2, 1, 2, 1, 2, 1, 2]
z = [1, 1, 1, 1, 2, 2, 2, 2]
fig = plt.figure()
ax = fig.add_subplot(111, projection="3d")
ax.set_xlim3d(0, 3)
ax.set_ylim3d(0, 3)
ax.set_zlim3d(0, 3)
ax.scatter(x, y, z)

plt.show()

import numpy as np

import matplotlib.pyplot as plt

from mpl_toolkits.mplot3d import Axes3D

x = [1, 1, 2, 2, 1, 1, 2, 2]

y = [1, 2, 1, 2, 1, 2, 1, 2]

z = [1, 1, 1, 1, 2, 2, 2, 2]

fig = plt.figure()

ax = fig.add_subplot(111, projection="3d")

ax.set_xlim3d(0, 3)

ax.set_ylim3d(0, 3)

ax.set_zlim3d(0, 3)

ax.scatter(x, y, z)

plt.show()

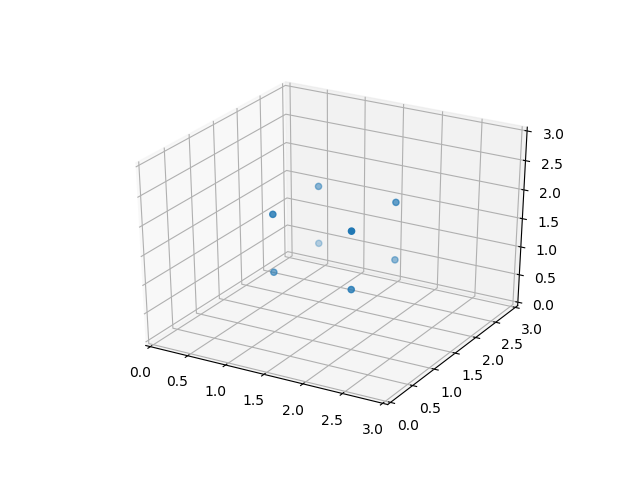
このコードの概要は以下の通り。

8つの頂点の座標の準備
- x, y, zの座標ごとに配列で準備
figureオブジェクトの取得
axesオブジェクトの取得
- axesオブジェクトの取得
- 3次元とするためにfig.add_subplot(111, projection="3d")としている
x,y,z軸の範囲を設定
- 3次元用のメソッドaxes.set_xlim3d(min, max)などで指定
点の表示
- axes.scatter(x, y, z)と3次元座標で指定

なお、上記の表示結果はマウスでドラッグして回転することができる。

`plot`～曲線の表示

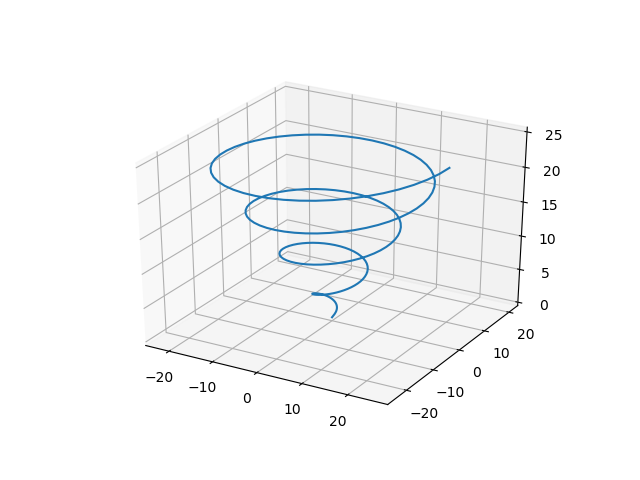
Axes3D.plot(x, y, z)によって、3次元空間内に曲線を描く。

以下の例は、パラメータ表示された以下の曲線を描いている。

(1) $\begin{align*} x = t \cos t,\quad y = t \sin t,\quad z = t \qquad (0 \le t \le 8 \pi) \end{align*}$

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

t = np.linspace(0, 8 * np.pi, num=200)
x = t * np.cos(t)
y = t * np.sin(t)
z = t

fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')

ax.plot(x, y, z)

plt.show()

import numpy as np

import matplotlib.pyplot as plt

from mpl_toolkits.mplot3d import Axes3D

t = np.linspace(0, 8 * np.pi, num=200)

x = t * np.cos(t)

y = t * np.sin(t)

z = t

fig = plt.figure()

ax = fig.add_subplot(111, projection='3d')

ax.plot(x, y, z)

plt.show()

`plot_wireframe/plot_sufrace`～曲面の表示

meshgrideで生成した座標面に対するf(x, y)の位置を使って、3次元の曲面を描く。plot_wireframeはワイヤーフレーム、plot_surfaceはワイヤーフレームの中の面が塗りつぶされる。以下の例では、z = x² + y²の関数の形状を、ワイヤーフレームと曲面で描く。

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

x = np.linspace(-1, 1, 20)
y = np.linspace(-1, 1, 20)
x, y = np.meshgrid(x, y)
z = x**2 + y**2

h_ticks = np.linspace(-1, 1, 5)
v_ticks = np.linspace(0, 2, 5)

fig = plt.figure(figsize=(12, 5))

ax1 = fig.add_subplot(121, projection="3d")
ax1.set_xticks(h_ticks)
ax1.set_yticks(h_ticks)
ax1.set_zticks(v_ticks)
ax1.plot_wireframe(x, y, z)

ax2 = fig.add_subplot(122, projection="3d")
ax2.set_xticks(h_ticks)
ax2.set_yticks(h_ticks)
ax2.set_zticks(v_ticks)
ax2.plot_surface(x, y, z)

plt.show()

import numpy as np

import matplotlib.pyplot as plt

from mpl_toolkits.mplot3d import Axes3D

x = np.linspace(-1, 1, 20)

y = np.linspace(-1, 1, 20)

x, y = np.meshgrid(x, y)

z = x**2 + y**2

h_ticks = np.linspace(-1, 1, 5)

v_ticks = np.linspace(0, 2, 5)

fig = plt.figure(figsize=(12, 5))

ax1 = fig.add_subplot(121, projection="3d")

ax1.set_xticks(h_ticks)

ax1.set_yticks(h_ticks)

ax1.set_zticks(v_ticks)

ax1.plot_wireframe(x, y, z)

ax2 = fig.add_subplot(122, projection="3d")

ax2.set_xticks(h_ticks)

ax2.set_yticks(h_ticks)

ax2.set_zticks(v_ticks)

ax2.plot_surface(x, y, z)

plt.show()

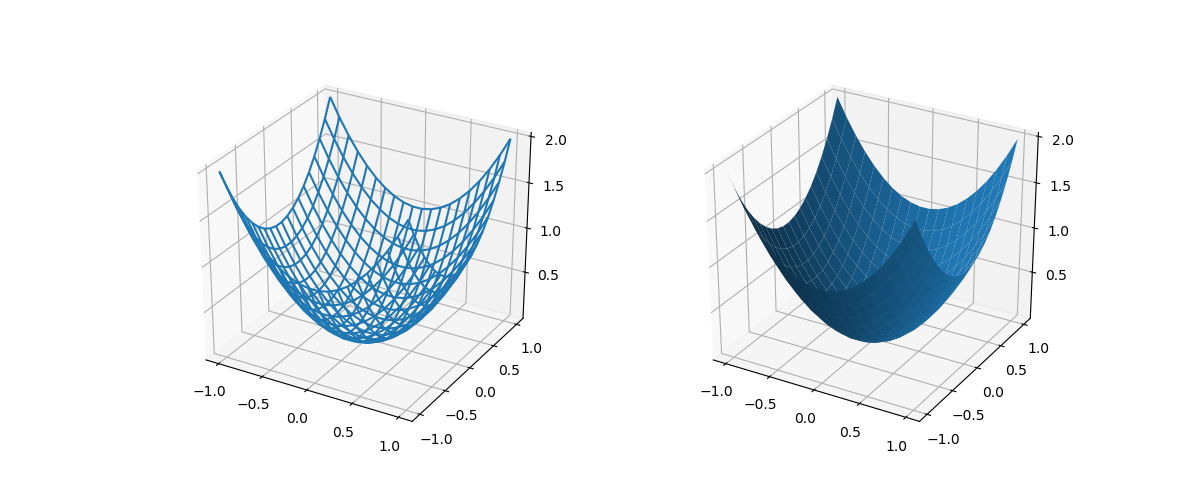
このコードの概要は以下の通り。

表示させる放物面の準備
1. x,yの軸座標を生成
2. numpy.meshgrid()関数で全格子点の座標を生成
3. 格子点座標に対するzの値を計算
x,y軸の軸目盛をhticks、z軸の軸目盛をvticksとして準備
figureの生成
axesの1つ目を生成し、ワイヤーフレーム表示
1. x,y,z軸の軸目盛をaxes.set_xticks()などのメソッドで設定
2. ワイヤーフレームの描画ax1.plot_wireframe(x, y, z)
axesの2つ目を生成し、曲面表示
1. x,y,z軸の軸目盛をaxes.set_xticks()などのメソッドで設定
2. 曲面の描画ax1.plot_surface(x, y, z)

コンターの表示

指定したz座標の位置に、f(x, y)のコンターを描く。以下の例では、z = x² + y²の関数の曲面を描き、z=0の面にコンターを描く。

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

x = np.linspace(-1, 1, 50)
y = np.linspace(-1, 1, 50)
x, y = np.meshgrid(x, y)
z3 = np.sqrt(x**2 + y**2)
z4 = np.abs(x) + np.abs(y)

h_ticks = np.linspace(-1, 1, 5)
v_ticks = np.linspace(0, 2, 5)

fig = plt.figure(figsize=(12, 5))

ax3 = fig.add_subplot(121, projection="3d")
ax3.set_xticks(h_ticks)
ax3.set_yticks(h_ticks)
ax3.set_zticks(v_ticks)
ax3.plot_surface(x, y, z3)
ax3.contour(x, y, z3, offset=0)

ax4 = fig.add_subplot(122, projection="3d")
ax4.set_xticks(h_ticks)
ax4.set_yticks(h_ticks)
ax4.set_zticks(v_ticks)
ax4.plot_surface(x, y, z4)
ax4.contour(x, y, z4, offset=0)

plt.show()

import numpy as np

import matplotlib.pyplot as plt

from mpl_toolkits.mplot3d import Axes3D

x = np.linspace(-1, 1, 50)

y = np.linspace(-1, 1, 50)

x, y = np.meshgrid(x, y)

z3 = np.sqrt(x**2 + y**2)

z4 = np.abs(x) + np.abs(y)

h_ticks = np.linspace(-1, 1, 5)

v_ticks = np.linspace(0, 2, 5)

fig = plt.figure(figsize=(12, 5))

ax3 = fig.add_subplot(121, projection="3d")

ax3.set_xticks(h_ticks)

ax3.set_yticks(h_ticks)

ax3.set_zticks(v_ticks)

ax3.plot_surface(x, y, z3)

ax3.contour(x, y, z3, offset=0)

ax4 = fig.add_subplot(122, projection="3d")

ax4.set_xticks(h_ticks)

ax4.set_yticks(h_ticks)

ax4.set_zticks(v_ticks)

ax4.plot_surface(x, y, z4)

ax4.contour(x, y, z4, offset=0)

plt.show()

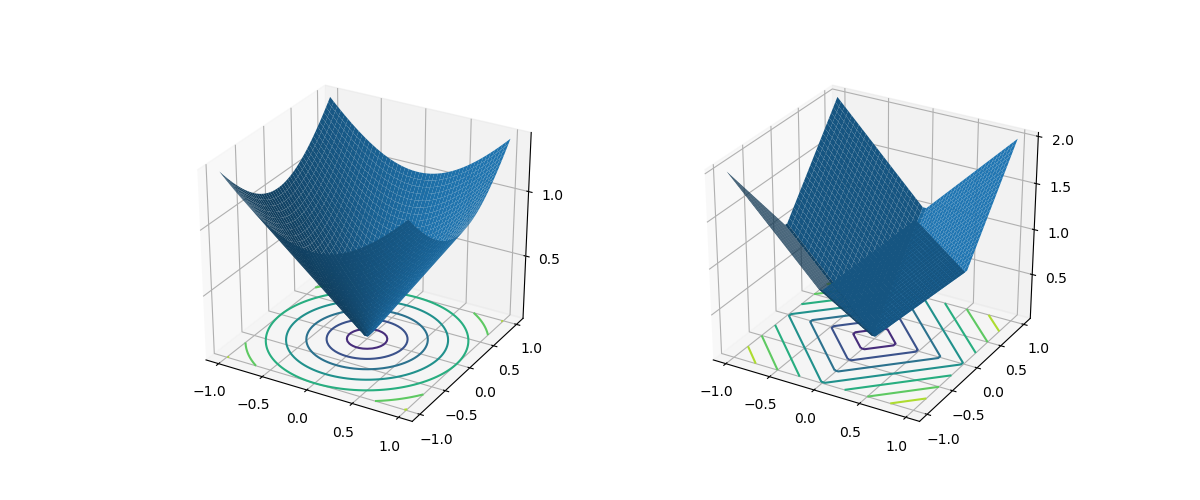
このコードの手順は上の曲面の表示とほぼ同じで、上記と異なる点は以下の通り。

2つの関数のコンターを比べるのに、xy平面上の点の原点からのL2ノルムとL1ノルムを使っている。
axes.contour()関数でコンターを描画している。
- contour(x, y, z, offset)のoffsetは、コンターを表示する平面のzの値で指定

TauStation

mplot3d.Axes3D – 3次元グラフの概要

概要

各種描画処理

`scatter`～点の表示

`plot`～曲線の表示

`plot_wireframe/plot_sufrace`～曲面の表示

コンターの表示

コメントを残すコメントをキャンセル

概要

各種描画処理

scatter～点の表示

plot～曲線の表示

plot_wireframe/plot_sufrace～曲面の表示

コンターの表示

コメントを残す コメントをキャンセル

`scatter`～点の表示

`plot`～曲線の表示

`plot_wireframe/plot_sufrace`～曲面の表示

コメントを残すコメントをキャンセル