正則化の意味～制約条件付最適化

/ tau / コメントする

疑　問

L2ノルムによるRidge回帰やL1ノルムによるLasso回帰に登場する罰則項。Lpノルムで表現すると次のようになる。

(1)   \begin{equation*} L(\boldsymbol{w}) = E(\boldsymbol{w}) + \alpha \sum_i |w_i|^p \end{equation*}

ここでEは正則化がない場合の下の損失関数、w=(w1, … , wm)は特徴量に対する重みでLは正則化考慮後の損失関数。

このLを最小となるようなwを計算していくことになるのだが、多くの文献やサイトでL1正則化やL2正則化を説明するのに次のような図を使って、制約条件付きの最小化問題としている。

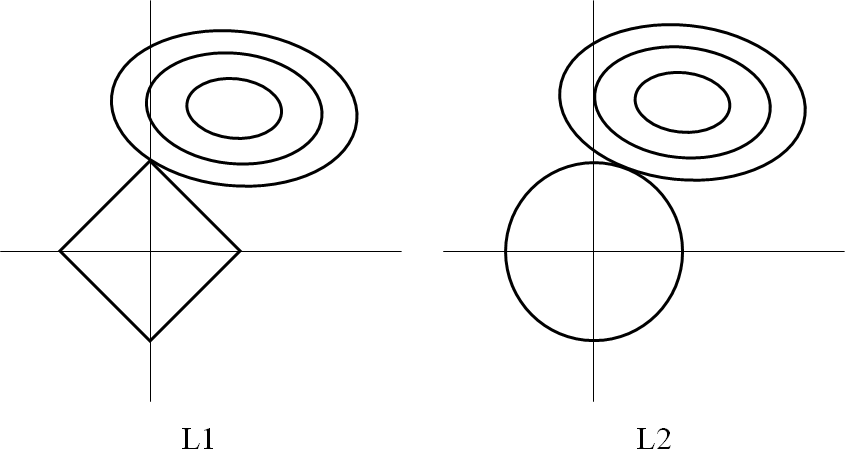
確かに式(1)の形はLagrrangeの未定乗数法に似ているのだが、ここで分からなくなるのが、αがハイパーパラメーターとして設定される点である。未定乗数法の場合、wとαを未知数として、Lを偏微分して解いていくが、ここではαは変数としては用いられない。

考え方

まず、以下のように重みwに対する制約を設定する。

(2)   \begin{equation*} \sum_i |w_i|^p \le \frac{1}{\mu} \qquad (\mu > 0) \end{equation*}

これは、重みのノルムが高々1/μであることを意味している。これを0以下の制約条件として以下のように変形する。

(3)   \begin{equation*} g(\boldsymbol{w}) = \mu \sum_i |w_i|^p - 1 \le 0 \end{equation*}

一般化するとa\sum |w_i|^p + bの形になるが、不等式の両辺をaで割ることで、このような表現とすることは差し支えない。

これを制約条件として、元々の損失関数E(w)を最小化するため、λを導入して不等式制約条件付きのLagrangeの未定乗数法の問題を立てる。

(4)   \begin{align*} &\mathrm{minimize} \quad E(\boldsymbol{w}) \\ &\mathrm{subject~to} \quad g(\boldsymbol{w}) = \mu \sum_i |w_i|^p - 1 \le 0 \\ &\rightarrow \quad M(\boldsymbol{w}, \lambda) = E(\boldsymbol{w}) - \lambda \left( \mu \sum_i |w_i|^p - 1 \right) \end{align*}

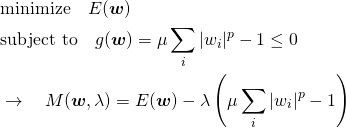
ここでKKT条件からλ ≤ 0となるので、ξ = −λ ≥ 0を導入して、以下のように表す。

(5)   \begin{align*} M(\boldsymbol{w}, \lambda) = E(\boldsymbol{w}) + \xi \left( \mu \sum_i |w_i|^p - 1 \right) \end{align*}

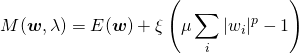
以降、冒頭の正則化の式と上記の最小化問題の式を並べる。

(6)   \begin{align*} &L(\boldsymbol{w}) = E(\boldsymbol{w}) + \alpha \sum_i |w_i|^p \\ &M(\boldsymbol{w}, \xi) = E(\boldsymbol{w}) + \xi \left( \mu \sum_i |w_i|^p - 1 \right) \end{align*}

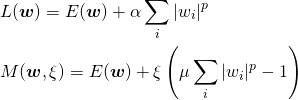
これらをwiで偏微分する。

(7)   \begin{align*} &\frac{\partial L}{\partial w_i} = \frac{\partial E}{\partial w_i} + \alpha \frac{d |w_i|^p}{d w_i} \\ &\frac{\partial M}{\partial w_i} = \frac{\partial E}{\partial w_i} + \xi \mu \frac{d |w_i|^p}{d w_i} \end{align*}

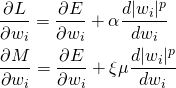
上式から、wに関しては2つの問題は等価と言える。しかしながら、Lの最小化についてはwの解が求まるのに対して、Mの最小化で解を確定するためには、ξを未知数としてこれについても偏微分をとり、未知数と方程式を1つ加えなければならない。どうしてLの最小化だけで最適解が定まるのか。

解　釈

ところで、αはハイパーパラメーターとして外部で設定するのであった。Lに関してはwiの個数分の未知数と方程式となり、wの解が確定する。すなわち、元の正則化の式を解くだけで「最適化された」係数のセットがw空間において1つに定まる。

ここからがミソで、wが求められるとこれを満たす制約条件の境界が定まり、同時に|w|pに対する制約も定まるというのがどうもこの計算の仕組みらしい。

そこで、αを設定した後のながれを追ってみる。

  • αを設定してLを最適化する
  • w = (w1, … , wm)が定まる
  • 点wを通る制約条件の境界g(w) = 0が定まる → Σ|wi|p = μ−1

すなわち、αを設定してLを最適化することで制約条件の境界g = 0が決定され、重みに対する制約の強さμも決まることになる。

なお、α = 0として罰則項の効果をなくす場合のほかは必ず制約条件の境界上で解を求めることになる。一般的なLagrangeの未定乗数法のように、与えられた制約条件と目的関数の関係によって純粋な極値問題となるということはない(後述する∇Eと∇gのgradientの向きの関係からも確認できる)。

ξやμはどのように定まるのか

本来なら生真面目に未定乗数法を解いて求めるはずのξはどこへ行ったのか。

  • 式(7)のノルム項の比較よりα = ξμ
  • αは事前に設定した値で、μはLの計算結果から導出されることから、ξ = μ/αも計算可能
  • なおMについて、点wにおいては∇E = −ξμ∇gが成り立っており、この点でEとgのgradientが平行(−ξμの符号から、両ベクトルは逆向き)

すなわち、ξはμと組み合わさって、境界条件における目的関数Eと制約条件gのgradientの比となっている。

μについては、α = ξμの関係から、αを大きくするとμも大きくなる傾向になりそうである。それにつれて式(2)から重みをより小さく制約する方向に効きそうである。ただしこの場合、ξも変動するので単純な比例関係にはならず、αの値を試行錯誤で変化させて学習効果を確認することになる。

参考サイト

本記事をまとめるにあたって、下記サイトが大変参考になったことに感謝したい。

過学習を防ぐ「正則化」とは？～○×（まるぺけ）つくろーどっとコム

 

 

 

コメントを残す

メールアドレスが公開されることはありません。 * が付いている欄は必須項目です