概要
scikit-learnの主成分分析モデル(PCA)をIrisデータに適用して、その挙動を確認する。
クラス分類のターゲットを用いていないにもかかわらず、少ない主成分でクラスがかなり明確に分類されることがわかる。
計算の手順
以下の手順・コードで計算した。
- 必要なパッケージをインポート
- Irisデータセットを準備
- データセットをスケーリング
StandardScalerで特徴量データを標準化している
- PCAモデルのインスタンスを生成
- 引数
n_componentsを指定せず、4つの特徴量全てを計算
- 引数
- モデルにデータを学習させる
fit()メソッドのみでよいが、後のグラフ化のためにfit_transform()メソッドを実行X_transに主成分によって変換したデータを格納
- 主成分やその寄与率を確認
- 主成分は
PCA.comonents_を、寄与率はPCA.explained_variance_ratio_を確認
- 主成分は
- 3つの主成分について3次元可視化
- 2つの主成分について2次元可視化
主成分と寄与率
以下に、主成分と寄与率を計算するまでのコードを示す。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 |
import numpy as np import pandas as pd import matplotlib.pyplot as plt from sklearn.datasets import load_iris from sklearn.preprocessing import StandardScaler from sklearn.decomposition import PCA from mpl_toolkits.mplot3d import Axes3D iris_data = load_iris() X = iris_data['data'] y = iris_data['target'] feature_names = iris_data['feature_names'] target_names = iris_data['target_names'] X_scaled = StandardScaler().fit_transform(X) pca = PCA() X_trans = pca.fit_transform(X_scaled) print(pd.DataFrame(pca.components_, columns=feature_names)) # sepal length (cm) sepal width (cm) petal length (cm) petal width (cm) # 0 0.521066 -0.269347 0.580413 0.564857 # 1 0.377418 0.923296 0.024492 0.066942 # 2 -0.719566 0.244382 0.142126 0.634273 # 3 -0.261286 0.123510 0.801449 -0.523597 print(pca.explained_variance_ratio_) # [0.72962445 0.22850762 0.03668922 0.00517871] |
寄与率の方を見てみると、第1主成分で約73%、第2主成分で23 %と、2つの主成分で特徴をほぼ説明しきっている(第3、第4主成分の寄与はほとんど無視できる)。
第1主成分の各要素の符号を見てみる。萼の長さ、花弁の長さと幅は同程度でプラス方向に効いていて、萼の幅はマイナス方向の効果を持っている。このことから、萼の細長さと花弁の全体的な大きさによって、アヤメの花が特徴づけられていると考えられる。また第2主成分は、萼の幅で殆ど特徴が決まっている。
可視化
3次元
4つの主成分のうち3つについて3次元で可視化してみると、3つのアヤメの種類がかなりきれいに分離されているのがわかる。
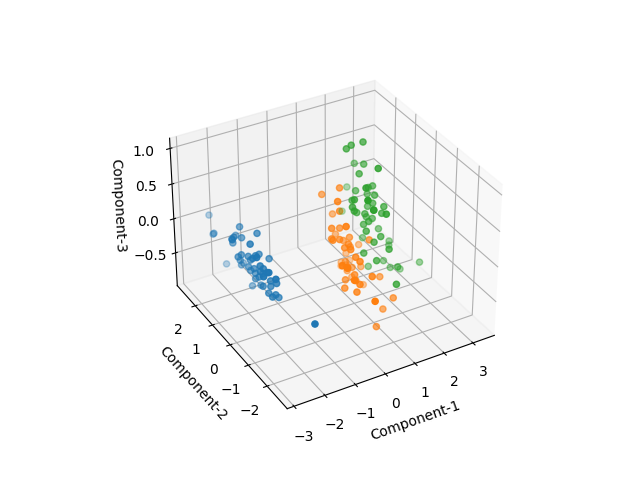
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
fig, ax = plt.subplots(subplot_kw=dict(projection='3d')) X0 = X_trans[y==0] X1 = X_trans[y==1] X2 = X_trans[y==2] ax.scatter(X0[:, 0], X0[:, 1], X0[:, 2]) ax.scatter(X1[:, 0], X1[:, 1], X1[:, 2]) ax.scatter(X2[:, 0], X2[:, 1], X2[:, 2]) ax.set_xlabel("Component-1") ax.set_ylabel("Component-2") ax.set_zlabel("Component-3") plt.show() |
2次元
第2主成分まででほとんどの特徴を説明できそうなので、2次元の散布図で表示してみる。
実際、2つの主成分だけでかなりきれいに3つのクラスが分かれている。少し重なっている部分があるが、先の主成分を3つの3次元グラフで傾きを調整すると、より明確にクラスが分けられる。
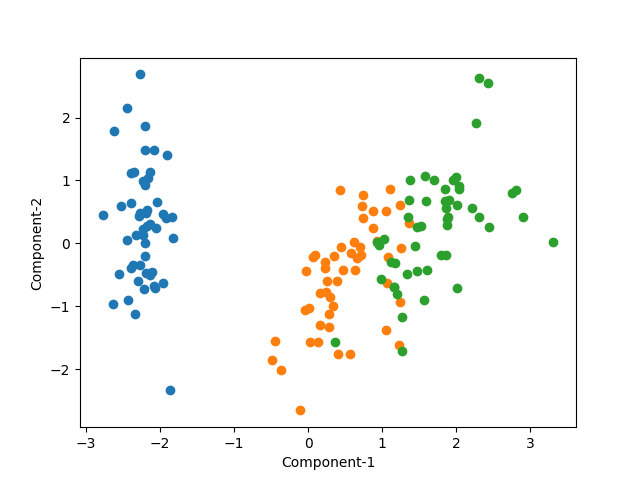
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
pca = PCA(n_components=2) X_trans = pca.fit_transform(X_scaled) print(pd.DataFrame(pca.components_, columns=feature_names)) print(pca.explained_variance_ratio_) fig, ax = plt.subplots() X0 = X_trans[y==0] X1 = X_trans[y==1] X2 = X_trans[y==2] ax.scatter(X0[:, 0], X0[:, 1]) ax.scatter(X1[:, 0], X1[:, 1]) ax.scatter(X2[:, 0], X2[:, 1]) ax.set_xlabel("Component-1") ax.set_ylabel("Component-2") plt.show() |
なお今回の計算では、PCAのモデルインスタンス生成時にn_components=2としている。その結果は以下の通りで、1つ前の結果と同じ値になっている。
|
1 2 3 4 |
sepal length (cm) sepal width (cm) petal length (cm) petal width (cm) 0 0.521066 -0.269347 0.580413 0.564857 1 0.377418 0.923296 0.024492 0.066942 [0.72962445 0.22850762] |
主成分分析の特徴
IrisデータセットへのPCAの適用結果から、以下のようにまとめられる。
- 主成分分析の計算において、ターゲットのクラス分類は全く用いていない(特徴量データのみを用いている)
- ターゲットのクラス分類は、散布図を描くときの色分けにのみ利用している
- それにも関わらず、散布図において3つのクラスがかなりきれいに分離されている
- 特徴量の線形和に沿った分散の最大化、という問題設定で、その背後にあるアヤメの種類がうまく分類されている