概要

主成分分析(principal component analysis: PCA)は教師なし学習の手法の一つでもあり、その考え方は、特徴量の線形組み合わせの中で、最もデータの情報を多く含む組み合わせを発見し、それを主成分として分析を行うものである。

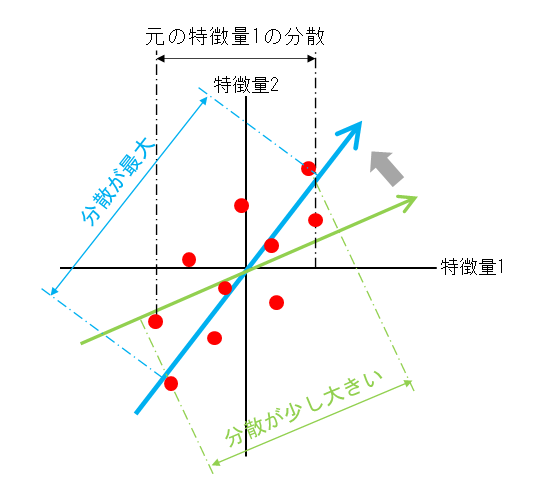
具体的には、特徴量空間の中でベクトルを考え、そのベクトル沿いのデータの分散が最も大きくなるようにベクトルを定める。その考え方と定式化については、主成分分析の定式化にまとめた。

クラス分類データへの適用

Irisデータセット

Irisデータセットにscikit-learnのPCAを適用した例。

PCA – Irisデータセット

教師なし学習として、クラス分類のターゲットデータを用いることなく、特徴量の分析だけでクラスがうまく分離できるような主成分が得られる。

Breast cancerデータセット

Breast cancerデータセットにscikit-learnのPCAを適用した例。

PCA – Breast cancerデータセット

Irisデータの場合と同じく、教師なし学習として、クラス分類のターゲットデータを用いることなく、特徴量の分析だけでクラスがうまく分離できるような主成分が得られる。

ここでは、主成分を構成する各特徴量の寄与をヒートマップによって視覚化している。

LFW peopleデータセット

著名人の顔画像データを集めたLFW peopleデータセットにscikit-learnのPCAを適用した例。

PCA – LFWデータセット

主成分の可視化、次元圧縮後の画像の再現など、様々な角度でPCAの特性を見ている。

回帰データへの適用

Boston house pricesデータセット

Boston house pricesデータセットにPCAを適用して、ターゲットが連続量で与えられた回帰系の問題への適用性を確認する。

PCA – Boston house pricesデータセット

このデータセットに関する限り、PCAで明確な関係は見いだせなかった。

なお、このデータセットには属性データが含まれ、前処理としてone-hot encodingを行っている。