概要
一様乱数を基にしたポアソン過程のシミュレーションは前にまとめたが、その時には表計算ソフトを使ったので操作性も悪く、限られたケースのみ計算したレベルだった。
その後、統計分析用のソフト”R“を少し勉強したので、より掘り下げた確認をしてみる。
前提条件と手法
平均すると10秒に1回、客が訪れる事象を考える。単位時間を1秒とすると、到着率は![]() となる。この条件下で、以下のことを確認する。
となる。この条件下で、以下のことを確認する。
- 一様乱数によったときの確率分布
- 時系列上での到着時刻の分布~一様分布
- 到着時間間隔の分布~指数分布
- 到着数の分布~Poisson分布
- 時刻制御(time driven)によったときの各種確率分布
- 同上
- イベント制御(event driven)ときの各種確率分布
- 時系列上での到着時刻の分布~一様乱数
- 到着数の分布~Poisson分布
考え方
一様乱数による方法
下図のように、観測時間tの間で一度に一様乱数を発生させ、それを昇順にソートしたものを到着時刻の時系列データとする。
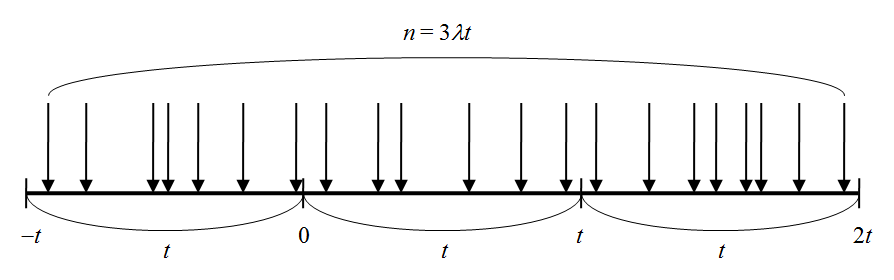
単に到着率λと観測時間tを掛けた平均到着数で乱数を発生させた場合、観測時間内の到着数が一定となってしまうため、観測時間と同じ時間幅で前後に余裕をとり、その中で一様乱数を発生させたうえで両端を切り落としている。
時刻制御とイベント制御
下図に、時刻制御(time driven)とイベント制御(event driven)の考え方の違いを比較して示している。
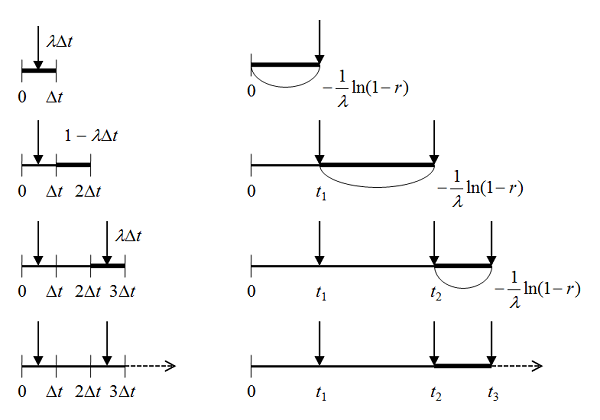
時刻制御については、観測時間を小さな時間間隔に区切って、区間ごとに到着確率に沿って到着の有無を決めながら、時刻を前に進めていく。
イベント制御の場合は、ポアソン過程で到着時間間隔が指数分布に従うことを利用して、指数乱数を発生させながら順次に到着時刻を算出していく。
関連リンク