標準正規分布 – TauStation

1 標準正規分布の使い方
- - 1.0.1 例題
2 標準正規分布の確率
- 2.1 典型的な値
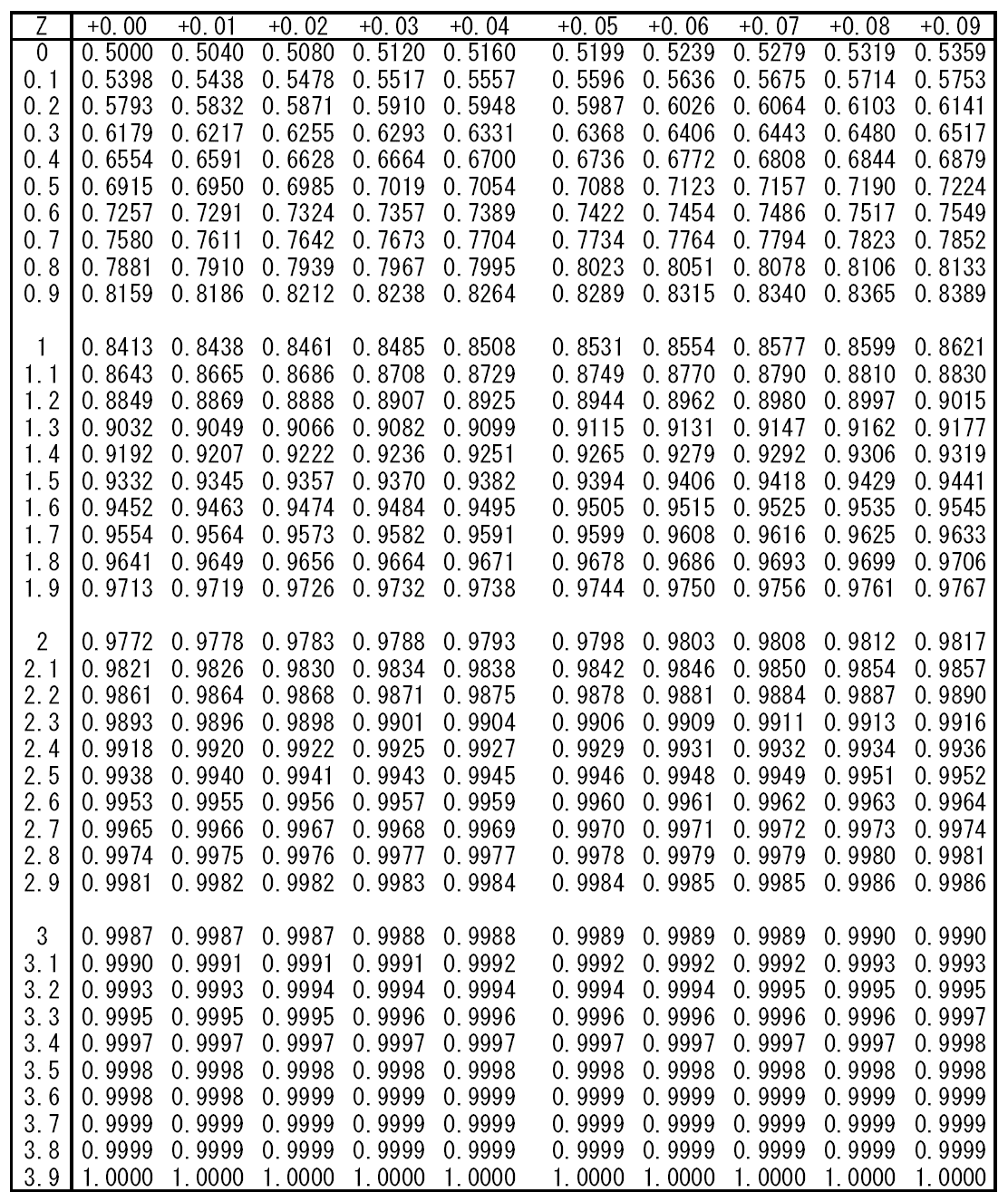
- 2.2 標準正規分布表

標準正規分布の使い方

平均 $\mu$ 、分散 $\sigma^2$ の正規分布 $N(\mu, \sigma^2)$ の確率密度関数は以下の通り。

(1) $\begin{equation*} f(x) = \frac{1}{\sqrt{2 \pi \sigma^2}} \exp \left( - \frac{(x - \mu)^2}{2 \sigma^2} \right) \end{equation*}$

この場合、 $X \leq t$ となる確率は以下のように表される。

(2) $\begin{equation*} \Pr(X \leq t) = \int_{-\infty}^{t} f(x) dx = \int_{-\infty}^{t} \frac{1}{\sqrt{2 \pi \sigma^2}} \exp \left( - \frac{(x - \mu)^2}{2 \sigma^2} \right) dx \end{equation*}$

ここで、確率変数を以下のように変換する。

(3) $\begin{equation*} Z = \frac{X - \mu}{\sigma} \quad , \quad u = \frac{t - \mu}{\sigma} \end{equation*}$

これを式(2)に適用し、 $dx = \sigma dz$ に留意して、

(4) $\begin{equation*} \Pr(X \leq t) &=& Pr \left( \frac{X - \mu}{\sigma} \leq \frac{t - \mu}{\sigma} \right) = \int_{-\infty}^{\frac{t - \mu}{\sigma}} \frac{1}{\sqrt{2 \pi}} \exp \left( - \frac{z^2}{2} \right) dz\end{equation*}$

標準正規分布の確率に対する確率変数 $u$ の値を覚えていれば、母集団の平均と標準偏差が与えられたとき、上記の変数変換を行って、確率値を得ることができる。

例題

厚生労働省による「平成29年国民健康・栄養調査報告」によると、26歳～29歳の日本人男性の身長は、平均が171.0cm、標準偏差が5.8cmとなっている。この年代層で身長が180cmを超える確率は、

(5) $\begin{equation*} Pr(X > 180) = Pr \left(Z > \frac{180 - 171.0}{5.8} \right) = Pr(Z > 1.5517) \end{equation*}$

このuの典型的な値と確率のセットを覚えておけば、確率を知ることができる。この場合は1.5より少し大きいので、超過確率は6％程度とわかる（より正確には6.04％）。

$u$ が0.5なら3割程度、1なら16%、1.5で6.7%になる。

逆に超過確率25%なら $u$ =0.67、10%なら1.28、5%（両側90%以内）で1.64、2.5%（両側95%以内）なら1.96。

標準正規分布の確率

典型的な値

標準正規分布の $Z$ に対する確率 $\Pr(Z \leq u)$ の $u$ に対する確率は標準正規分布表で与えられているが、以下の値は覚えておくとよい。

z	$\Pr(Z > u)$	$\Pr(-u \leq Z \leq u)$
0.5	0.31	0.38
0.67449 (0.67)	0.25	0.5
0.84162	0.2	0.6
1	0.16	0.68
1.03643	0.15	0.7
1.15035	0.125	0.75
1.28155 (1.28)	0.1	0.8
1.5	0.067	0.87
1.64485 (1.64)	0.05	0.9
1.95996 (1.96)	0.025	0.95
2	0.023	0.95
2.32635 (2.32)	0.01	0.98
2.57584 (2.58)	0.005	0.99

標準正規分布表

std_norm_dist_table

標準正規分布の使い方

例題

標準正規分布の確率

典型的な値

標準正規分布表

コメントを残す コメントをキャンセル

コメントを残すコメントをキャンセル