t分布 – TauStation

概要

t分布は連続確率分布の1つで、以下のような場合に用いられる。

正規分布する母集団の平均と分散が未知で標本サイズが小さい場合に平均を推定
2つの平均値の差の統計的有意性に対するt検定

サンプルX₁, …, X_nが平均μの正規分布に従うとし、標本平均 $\overline{X}$ と不偏分散s²が以下であるとする。

(1) $\begin{align*} \overline{X}_n &= \frac{1}{n} \sum_{i=1}^n X_i \\ {s^2}_n &= \frac{1}{n - 1} \sum_{i=1}^n \left( X_i - \overline{X} \right) \end{align*}$

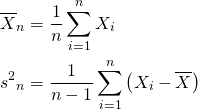
ここで以下の変数（t値）を考える。

(2) $\begin{equation*} t = \frac{\overline{X}_n - \mu}{\sqrt{{s^2}_n / n}} \end{equation*}$

このとき、上記のt値は以下の確率分布でν = n − 1としたものに従うことが知られている。

(3) $\begin{equation*} f(t; \nu) = \dfrac{\Gamma \left( \dfrac{\nu + 1}{2}\right) }{\sqrt{\nu \pi} \Gamma \left( {\dfrac{\nu}{2}}\right)} \left( 1 + \dfrac{t^2}{\nu} \right)^{- \dfrac{\nu + 1}{2} \end{equation*}$

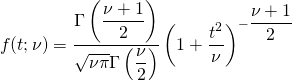
この確率分布はstudentのt分布と呼ばれ、Γはガンマ関数。

自由度と確率分布の関係

t分布の自由度νを変化させて確率分布を描いてみる。

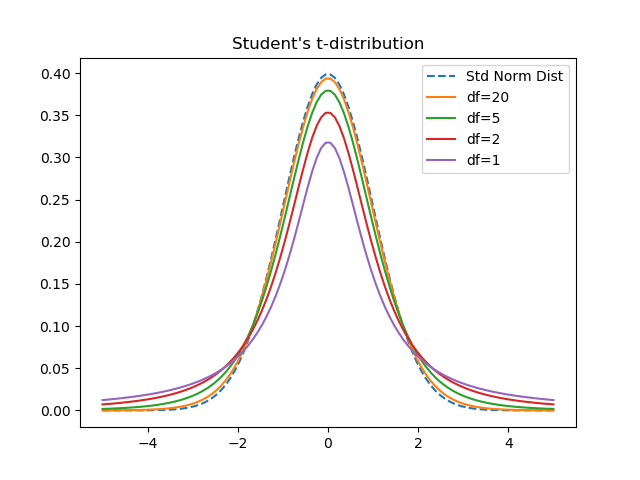
自由度20あたりでかなり標準積分布に近くなっていることがわかる。自由度1～20に対して片側確率が10%, 5%, 2.5%, 1%, 0.5%ととなるzの値を計算すると以下のようになる。

t分布表

以下に、自由度1 ～20に対して、いくつかの片側確率に対するt値の表を示す（Pr(t) > α)となるt値）。

自由度が20くらいになるとかなり標準正規分布に近い形になるが、zの値は有効数値2桁目で違ってくる。自由度が700くらいで何とか3桁目まで標準正規分布の値と同じになる。

ν	0.1	0.05	0.025	0.01	0.005
1	3.078	6.314	12.706	31.821	63.657
2	1.886	2.920	4.303	6.965	9.925
3	1.638	2.353	3.182	4.541	5.841
4	1.533	2.132	2.776	3.747	4.604
5	1.476	2.015	2.571	3.365	4.032
6	1.440	1.943	2.447	3.143	3.707
7	1.415	1.895	2.365	2.998	3.499
8	1.397	1.860	2.306	2.896	3.355
9	1.383	1.833	2.262	2.821	3.250
10	1.372	1.812	2.228	2.764	3.169
11	1.363	1.796	2.201	2.718	3.106
12	1.356	1.782	2.179	2.681	3.055
13	1.350	1.771	2.160	2.650	3.012
14	1.345	1.761	2.145	2.624	2.977
15	1.341	1.753	2.131	2.602	2.947
16	1.337	1.746	2.120	2.583	2.921
17	1.333	1.740	2.110	2.567	2.898
18	1.330	1.734	2.101	2.552	2.878
19	1.328	1.729	2.093	2.539	2.861
20	1.325	1.725	2.086	2.528	2.845
N(0, 1)	1.282	1.645	1.960	2.326	2.576

なお、これらの値はPythonのscipy.statsからt分布と正規分布の関数を呼び出して得られる。

import numpy as np
import scipy.stats as stats

probs = np.array([0.1, 0.05, 0.025, 0.01, 0.005])

fmt_header = "{0:>2}{1[0]:>7}{1[1]:>7}{1[2]:>7}{1[3]:>7}{1[4]:>7}"
fmt_data = "{0:2d}{1[0]:7.3f}{1[1]:7.3f}{1[2]:7.3f}{1[3]:7.3f}{1[4]:7.3f}"
fmt_footer = "{0:>2}{1[0]:7.3f}{1[1]:7.3f}{1[2]:7.3f}{1[3]:7.3f}{1[4]:7.3f}"

print(fmt_header.format(" ", probs))
for df in range(1, 21):
    print(fmt_data.format(df, -stats.t.ppf(probs, df=df)))
print()
print(fmt_footer.format("N", -stats.norm.ppf(probs, loc=0, scale=1)))

import numpy as np

import scipy.stats as stats

probs = np.array([0.1, 0.05, 0.025, 0.01, 0.005])

fmt_header = "{0:>2}{1[0]:>7}{1[1]:>7}{1[2]:>7}{1[3]:>7}{1[4]:>7}"

fmt_data = "{0:2d}{1[0]:7.3f}{1[1]:7.3f}{1[2]:7.3f}{1[3]:7.3f}{1[4]:7.3f}"

fmt_footer = "{0:>2}{1[0]:7.3f}{1[1]:7.3f}{1[2]:7.3f}{1[3]:7.3f}{1[4]:7.3f}"

print(fmt_header.format(" ", probs))

for df in range(1, 21):

print(fmt_data.format(df, -stats.t.ppf(probs, df=df)))

print()

print(fmt_footer.format("N", -stats.norm.ppf(probs, loc=0, scale=1)))

概要

自由度と確率分布の関係

t分布表

コメントを残す コメントをキャンセル

コメントを残すコメントをキャンセル