import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_circles
from sklearn.model_selection import train_test_split
from sklearn.ensemble import GradientBoostingClassifier
f0min, f0max = -1.5, 1.5
f1min, f1max = -1.75, 1.5
X, y = make_circles(noise=0.25, factor=0.5, random_state=1)
X_train, X_test, y_train, y_test =\
train_test_split(X, y, random_state=0)
gb = GradientBoostingClassifier(random_state=0)
gb.fit(X_train, y_train)
print("X_test.shape : {}".format(X_test.shape))
print("Decision function shape: {}".format(
gb.decision_function(X_test).shape))
fig, axs = plt.subplots(1, 2, figsize=(10, 4.8))
color0, color1 = 'tab:blue', 'tab:orange'
f0 = np.linspace(f0min, f0max, 200)
f1 = np.linspace(f1min, f1max, 200)
f0, f1 = np.meshgrid(f0, f1)
F = np.c_[f0.reshape(-1, 1), f1.reshape(-1, 1)]
pred = gb.predict(F).reshape(f0.shape)
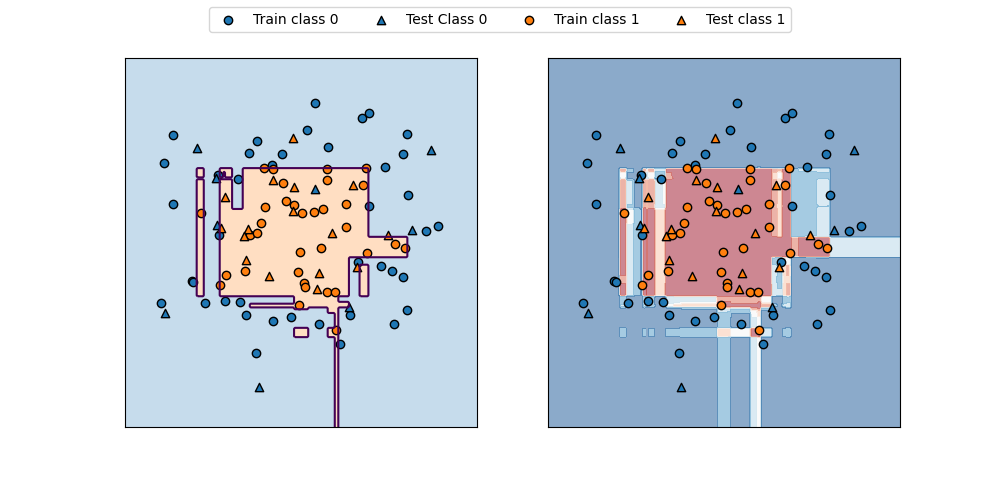
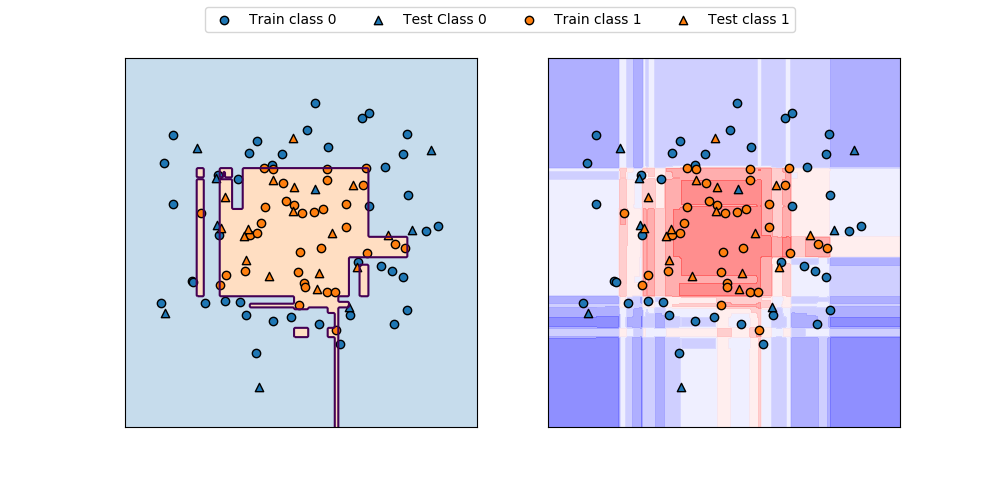
axs[0].contour(f0, f1, pred, levels=[0.5])
axs[0].contourf(f0, f1, pred, levels=1, colors=[color0, color1], alpha=0.25)
decision = gb.decision_function(F).reshape(f0.shape)
axs[1].contourf(f0, f1, decision, alpha=0.5, cmap='bwr')
for ax in axs:
ax.scatter(X_train[y_train==0][:, 0], X_train[y_train==0][:, 1], marker='o', fc=color0, ec='k', label="Train class 0")
ax.scatter(X_test[y_test==0][:, 0], X_test[y_test==0][:, 1], marker='^', fc=color0, ec='k', label="Test Class 0")
ax.scatter(X_train[y_train==1][:, 0], X_train[y_train==1][:, 1], marker='o', fc=color1, ec='k', label="Train class 1")
ax.scatter(X_test[y_test==1][:, 0], X_test[y_test==1][:, 1], marker='^', fc=color1, ec='k', label="Test class 1")
ax.set_xlim(f0min, f0max)
ax.set_ylim(f1min, f1max)
ax.tick_params(left=False, bottom=False, labelleft=False, labelbottom=False)
handles, labels = axs[0].get_legend_handles_labels()
fig.legend(handles, labels, ncol=4, loc='upper center')
plt.show()